Biased graph
Encyclopedia
In mathematics
, a biased graph is a graph
with a list of distinguished circles (edge sets of simple cycles), such that if two circles in the list are contained in a theta graph
, then so is the third circle of the theta graph. A biased graph is a generalization of the combinatorial essentials of a gain graph
and in particular of a signed graph.
Formally, a biased graph Ω is a pair (G, B) where B is a linear class of circles; this by definition is a class of circles that satisfies the theta-graph property mentioned above.
A subgraph or edge set whose circles are all in B (and which contains no half-edges
) is called balanced. For instance, a circle belonging to B is balanced and one that does not belong to B is unbalanced.
Biased graphs are interesting mostly because of their matroid
s, but also because of their connection with multiary quasigroups. See below.
(one endpoint) and loose edges
(no endpoints). The edges with two endpoints are of two kinds: a link has two distinct endpoints, while a loop has two coinciding endpoints.
Linear classes of circles are a special case of linear subclasses of circuits in a matroid
.
of a biased graph Ω = (G, B) is the result of any sequence of taking subgraphs and contracting edge sets. For biased graphs, as for graphs, it suffices to take a subgraph (which may be the whole graph) and then contract an edge set (which may be the empty set).
A subgraph of Ω consists of a subgraph H of the underlying graph G, with balanced circle class consisting of those balanced circles that are in H. The deletion of an edge set S, written Ω − S, is the subgraph with all vertices and all edges except those of S.
Contraction of Ω is relatively complicated. To contract one edge e, the procedure depends on the kind of edge e is. If e is a link, contract it in G. A circle C in the contraction G/e is balanced if either C or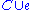
is a balanced circle of G. If e is a balanced loop or a loose edge, it is simply deleted. If it is an unbalanced loop or a half-edge, it and its vertex v are deleted; each other edge with v as an endpoint loses that endpoint, so a link with v as one endpoint becomes a half-edge at its other endpoint, while a loop or half-edge at v becomes a loose edge.
In the contraction Ω/S by an arbitrary edge set S, the edge set is E − S. (We let G = (V, E).) The vertex set is the class of vertex sets of balanced components of the subgraph (V, S) of Ω. That is, if (V, S) has balanced components with vertex sets V1, ..., Vk, then Ω/S has k vertices V1, ..., Vk . An edge e of Ω, not in S, becomes an edge of Ω/S and each endpoint vi of e in Ω that belongs to some Vi becomes the endpoint Vi of e in Ω/S ; thus, an endpoint of e that is not in a balanced component of (V, S) disappears. An edge with all endpoints in unbalanced components of (V, S) becomes a loose edge in the contraction. An edge with only one endpoint in a balanced component of (V, S) becomes a half-edge. An edge with two endpoints that belong to different balanced components becomes a link, and an edge with two endpoints that belong to the same balanced component becomes a loop.
associated with a biased graph, both of which generalize the cycle matroid of a graph (Zaslavsky, 1991).
The circuits of the matroid are called frame circuits or bias circuits. There are four kinds. One is a balanced circle. Two other kinds are a pair of unbalanced circles together with a connecting simple path, such that the two circles are either disjoint (then the connecting path has one end in common with each circle and is otherwise disjoint from both) or share just a single common vertex (in this case the connecting path is that single vertex). The fourth kind of circuit is a theta graph in which every circle is unbalanced.
The rank of an edge set S is n − b, where n is the number of vertices of G and b is the number of balanced components of S, counting isolated vertices as balanced components.
Minors of the frame matroid agree with minors of the biased graph; that is, M(Ω−S) = M(Ω)−S and M(Ω/S) = M(Ω)/S.
Frame matroids generalize the Dowling geometries
associated with a group (Dowling, 1973). The frame matroid of a 2Cn (a cycle of length n with doubled edges) which has no balanced digons is called a swirl. It is important in matroid structure theory.
An edge set is independent if each of its connected components contains either no circles or just one circle, which is unbalanced.
A circuit is a balanced circle, a pair of unbalanced circles that are either disjoint or have just a common vertex, or a theta graph whose circles are all unbalanced.
The rank of an edge set S is n − c + ε, where c is the number of components of S, counting isolated vertices, and ε is 0 if S is balanced and 1 if it is not.
Minors of the lift and extended lift matroids agree in part with minors of the biased graph. Deletions agree: L(Ω−S) = L(Ω)−S. Contractions agree only for balanced edge sets: M(Ω/S) = M(Ω)/S if S is balanced, but not if it is unbalanced. If S is unbalanced, M(Ω/S) = M(G)/S = M(G/S) where M of a graph denotes the ordinary graphic matroid.
The lift matroid of a 2Cn in which every digon is unbalanced is called a spike. Spikes are quite important in matroid structure theory.
), its combinatorial analog expanding a simple cycle of length n + 1 encodes an n-ary (multiary) quasigroup. It is possible to prove theorems about multiary quasigroups by means of biased graphs (Zaslavsky, t.a.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a biased graph is a graph
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
with a list of distinguished circles (edge sets of simple cycles), such that if two circles in the list are contained in a theta graph
Glossary of graph theory
Graph theory is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with current usage....
, then so is the third circle of the theta graph. A biased graph is a generalization of the combinatorial essentials of a gain graph
Gain graph
A gain graph is a graph whose edges are labelled "invertibly", or "orientably", by elements of a group G. This means that, if an edge e in one direction has label g , then in the other direction it has label g −1...
and in particular of a signed graph.
Formally, a biased graph Ω is a pair (G, B) where B is a linear class of circles; this by definition is a class of circles that satisfies the theta-graph property mentioned above.
A subgraph or edge set whose circles are all in B (and which contains no half-edges
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
) is called balanced. For instance, a circle belonging to B is balanced and one that does not belong to B is unbalanced.
Biased graphs are interesting mostly because of their matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
s, but also because of their connection with multiary quasigroups. See below.
Technical notes
A biased graph may have half-edgesGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
(one endpoint) and loose edges
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
(no endpoints). The edges with two endpoints are of two kinds: a link has two distinct endpoints, while a loop has two coinciding endpoints.
Linear classes of circles are a special case of linear subclasses of circuits in a matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
.
Examples
- If every circle belongs to B, and there are no half-edges, Ω is balanced. A balanced biased graph is (for most purposes) essentially the same as an ordinary graph.
- If B is empty, Ω is called contrabalanced. Contrabalanced biased graphs are related to bicircular matroidBicircular matroidIn the mathematical subject of matroid theory, the bicircular matroid of a graph G is the matroid B whose points are the edges of G and whose independent sets are the edge sets of pseudoforests of G, that is, the edge sets in which each connected component contains at most one cycle...
s.
- If B consists of the circles of odd length, Ω is called antibalanced and is the biased graph obtained from an all-negative signed graph.
- The linear class B is additive, that is, closed under set sum (for sums that give a circle), if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
B is the class of positive circles of a signed graph.
- Ω may consist of a cycle of length n ≥ 3 with all edges doubled and such that no digonDigonIn geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...
(circle of length 2) is balanced. Call this a biased 2Cn . Such biased graphs lead to spikes and swirls (see Matroids, below).
- Some kinds of biased graph are obtained from gain graphGain graphA gain graph is a graph whose edges are labelled "invertibly", or "orientably", by elements of a group G. This means that, if an edge e in one direction has label g , then in the other direction it has label g −1...
s or are generalizations of special kinds of gain graph. The latter include biased expansion graphs, which generalize group expansion graphGain graphA gain graph is a graph whose edges are labelled "invertibly", or "orientably", by elements of a group G. This means that, if an edge e in one direction has label g , then in the other direction it has label g −1...
s.
Minors
A minorMinor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
of a biased graph Ω = (G, B) is the result of any sequence of taking subgraphs and contracting edge sets. For biased graphs, as for graphs, it suffices to take a subgraph (which may be the whole graph) and then contract an edge set (which may be the empty set).
A subgraph of Ω consists of a subgraph H of the underlying graph G, with balanced circle class consisting of those balanced circles that are in H. The deletion of an edge set S, written Ω − S, is the subgraph with all vertices and all edges except those of S.
Contraction of Ω is relatively complicated. To contract one edge e, the procedure depends on the kind of edge e is. If e is a link, contract it in G. A circle C in the contraction G/e is balanced if either C or
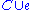is a balanced circle of G. If e is a balanced loop or a loose edge, it is simply deleted. If it is an unbalanced loop or a half-edge, it and its vertex v are deleted; each other edge with v as an endpoint loses that endpoint, so a link with v as one endpoint becomes a half-edge at its other endpoint, while a loop or half-edge at v becomes a loose edge.In the contraction Ω/S by an arbitrary edge set S, the edge set is E − S. (We let G = (V, E).) The vertex set is the class of vertex sets of balanced components of the subgraph (V, S) of Ω. That is, if (V, S) has balanced components with vertex sets V1, ..., Vk, then Ω/S has k vertices V1, ..., Vk . An edge e of Ω, not in S, becomes an edge of Ω/S and each endpoint vi of e in Ω that belongs to some Vi becomes the endpoint Vi of e in Ω/S ; thus, an endpoint of e that is not in a balanced component of (V, S) disappears. An edge with all endpoints in unbalanced components of (V, S) becomes a loose edge in the contraction. An edge with only one endpoint in a balanced component of (V, S) becomes a half-edge. An edge with two endpoints that belong to different balanced components becomes a link, and an edge with two endpoints that belong to the same balanced component becomes a loop.
Matroids
There are two kinds of matroidMatroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
associated with a biased graph, both of which generalize the cycle matroid of a graph (Zaslavsky, 1991).
The frame matroid
The frame matroid (sometimes called bias matroid) of a biased graph, M(Ω), (Zaslavsky, 1989) has for its ground set the edge set E. An edge set is independent if each component contains either no circles or just one circle, which is unbalanced. (In matroid theory a half-edge acts like an unbalanced loop and a loose edge acts like a balanced loop.) M(Ω) is a frame matroid in the abstract sense, meaning that it is a submatroid of a matroid in which, for at least one basis, the set of lines generated by pairs of basis elements covers the whole matroid. Conversely, every abstract frame matroid is the frame matroid of some biased graph.The circuits of the matroid are called frame circuits or bias circuits. There are four kinds. One is a balanced circle. Two other kinds are a pair of unbalanced circles together with a connecting simple path, such that the two circles are either disjoint (then the connecting path has one end in common with each circle and is otherwise disjoint from both) or share just a single common vertex (in this case the connecting path is that single vertex). The fourth kind of circuit is a theta graph in which every circle is unbalanced.
The rank of an edge set S is n − b, where n is the number of vertices of G and b is the number of balanced components of S, counting isolated vertices as balanced components.
Minors of the frame matroid agree with minors of the biased graph; that is, M(Ω−S) = M(Ω)−S and M(Ω/S) = M(Ω)/S.
Frame matroids generalize the Dowling geometries
Dowling geometry
In combinatorial mathematics, a Dowling geometry, named after Thomas A. Dowling, is a matroid associated with a group. There is a Dowling geometry of each rank for each group. If the rank is at least 3, the Dowling geometry uniquely determines the group...
associated with a group (Dowling, 1973). The frame matroid of a 2Cn (a cycle of length n with doubled edges) which has no balanced digons is called a swirl. It is important in matroid structure theory.
The lift matroid
The extended lift matroid L0(Ω) has for its ground set the set E0, which is the union of E with an extra point e0. The lift matroid L(Ω) is the extended lift matroid restricted to E. The extra point acts exactly like an unbalanced loop or a half-edge, so we describe only the lift matroid.An edge set is independent if each of its connected components contains either no circles or just one circle, which is unbalanced.
A circuit is a balanced circle, a pair of unbalanced circles that are either disjoint or have just a common vertex, or a theta graph whose circles are all unbalanced.
The rank of an edge set S is n − c + ε, where c is the number of components of S, counting isolated vertices, and ε is 0 if S is balanced and 1 if it is not.
Minors of the lift and extended lift matroids agree in part with minors of the biased graph. Deletions agree: L(Ω−S) = L(Ω)−S. Contractions agree only for balanced edge sets: M(Ω/S) = M(Ω)/S if S is balanced, but not if it is unbalanced. If S is unbalanced, M(Ω/S) = M(G)/S = M(G/S) where M of a graph denotes the ordinary graphic matroid.
The lift matroid of a 2Cn in which every digon is unbalanced is called a spike. Spikes are quite important in matroid structure theory.
Multiary quasigroups
Just as a group expansion of a complete graph Kn encodes the group (see Dowling geometryDowling geometry
In combinatorial mathematics, a Dowling geometry, named after Thomas A. Dowling, is a matroid associated with a group. There is a Dowling geometry of each rank for each group. If the rank is at least 3, the Dowling geometry uniquely determines the group...
), its combinatorial analog expanding a simple cycle of length n + 1 encodes an n-ary (multiary) quasigroup. It is possible to prove theorems about multiary quasigroups by means of biased graphs (Zaslavsky, t.a.)