
Constructive set theory
Encyclopedia
Constructive set theory is an approach to mathematical constructivism
following the program of axiomatic set theory. That is, it uses the usual first-order
language of classical set theory, and although of course the logic is constructive, there is no explicit use of constructive types. Rather, there are just sets, thus it can look very much like classical mathematics done on the most common foundations, namely the Zermelo–Fraenkel axioms (ZFC).
proposed a system of set theory based on intuitionistic logic taking the most common foundation, ZFC, and throwing away the axiom of choice (AC) and the law of the excluded middle (LEM), leaving everything else as is. However, different forms of some of the ZFC axioms which are equivalent in the classical setting are inequivalent in the constructive setting, and some forms imply LEM.
The system, which has come to be known as IZF, or Intuitionistic Zermelo–Fraenkel (ZF refers to ZFC without the axiom of choice), has the usual axioms of extensionality
, pairing
, union
, infinity
, separation and power set
. The axiom of regularity
is stated in the form of an axiom schema of set induction
. Also, while Myhill used the axiom schema of replacement
in his system, IZF usually stands for the version with collection.
While the axiom of replacement requires the relation φ to be a function over the set A (that is, for every x in A there is associated exactly one y), the axiom of collection does not: it merely requires there be associated at least one y, and it asserts the existence of a set which collects at least one such y for each such x. The axiom of regularity
as it is normally stated implies LEM, whereas the form of set induction does not. The formal statements of these two schemata are:
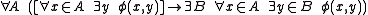
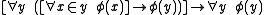
Adding LEM back to IZF results in ZF, as LEM makes collection equivalent to replacement and set induction equivalent to regularity.
. It allows formation of sets using the axiom of separation with any proposition, including ones which contain quantifiers which are not bounded. Thus new sets can be formed in terms of the universe of all sets. Additionally the power set axiom implies the existence of a set of truth values. In the presence of LEM, this set exists and has two elements. In the absence of it, the set of truth values is also considered impredicative.
to provide a formal foundation for Errett Bishop
's program of constructive mathematics. As he presented it, Myhill's system CST is a constructive first-order logic with three sorts
: natural numbers, function
s, and sets. The system is:
's constructive Zermelo-Fraenkel, or CZF, is essentially IZF with its impredicative features removed. It strengthens the collection scheme, and then drops the impredicative power set axiom and replaces it with another collection scheme. Finally the separation axiom is restricted, as in Myhill's CST. This theory has a relatively simple interpretation in a version of constructive type theory and has modest proof theoretic strength as well as a fairly direct constructive and predicative justification, while retaining the language of set theory. Adding LEM to this theory also recovers full ZF.
The collection axioms are:
Strong collection schema: This is the constructive replacement for the axiom schema of replacement
. It states that if φ is a binary relation
between sets which is total over a certain domain set (that is, it has at least one image of every element in the domain), then there exists a set which contains at least one image under φ of every element of the domain, and only images of elements of the domain. Formally, for any formula φ:

Subset collection schema: This is the constructive version of the power set axiom. Formally, for any formula φ:
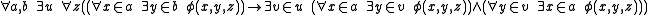
This is equivalent to a single and somewhat clearer axiom of fullness: between any two sets a and b, there is a set c which contains a total subrelation of any total relation between a and b that can be encoded as a set of ordered pair
s. Formally:
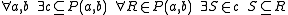
where the references to P(a,b) are defined by:


and some set-encoding of the ordered pair is assumed.
The axiom of fullness implies CST's axiom of exponentiation: given two sets, the collection of all total functions from one to the other is also in fact a set.
The remaining axioms of CZF are: the axioms of extensionality
, pairing
, union
, and infinity
are the same as in ZF; and set induction
and predicative separation
are the same as above.
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
following the program of axiomatic set theory. That is, it uses the usual first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
language of classical set theory, and although of course the logic is constructive, there is no explicit use of constructive types. Rather, there are just sets, thus it can look very much like classical mathematics done on the most common foundations, namely the Zermelo–Fraenkel axioms (ZFC).
Intuitionistic Zermelo–Fraenkel
In 1973, John MyhillJohn Myhill
John R. Myhill was a mathematician, born in 1923. He received his Ph.D. from Harvard University under Willard Van Orman Quine in 1949. He was professor at SUNY Buffalo from 1966 until his death in 1987...
proposed a system of set theory based on intuitionistic logic taking the most common foundation, ZFC, and throwing away the axiom of choice (AC) and the law of the excluded middle (LEM), leaving everything else as is. However, different forms of some of the ZFC axioms which are equivalent in the classical setting are inequivalent in the constructive setting, and some forms imply LEM.
The system, which has come to be known as IZF, or Intuitionistic Zermelo–Fraenkel (ZF refers to ZFC without the axiom of choice), has the usual axioms of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
, pairing
Axiom of pairing
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
, union
Axiom of union
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
, infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
, separation and power set
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
. The axiom of regularity
Axiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
is stated in the form of an axiom schema of set induction
Epsilon-induction
In mathematics, \in-induction is a variant of transfinite induction, which can be used in set theory to prove that all sets satisfy a given property P[x]. If the truth of the property for x follows from its truth for all elements of x, for every set x, then the property is true of all sets...
. Also, while Myhill used the axiom schema of replacement
Axiom schema of replacement
In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
in his system, IZF usually stands for the version with collection.
While the axiom of replacement requires the relation φ to be a function over the set A (that is, for every x in A there is associated exactly one y), the axiom of collection does not: it merely requires there be associated at least one y, and it asserts the existence of a set which collects at least one such y for each such x. The axiom of regularity
Axiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
as it is normally stated implies LEM, whereas the form of set induction does not. The formal statements of these two schemata are:
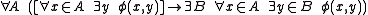
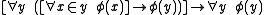
Adding LEM back to IZF results in ZF, as LEM makes collection equivalent to replacement and set induction equivalent to regularity.
Predicativity
While IZF is based on constructive rather than classical logic, it is considered impredicativeImpredicative
In mathematics and logic, impredicativity is the property of a self-referencing definition. More precisely, a definition is said to be impredicative if it invokes the set being defined, or another set which contains the thing being defined.Russell's paradox is a famous example of an impredicative...
. It allows formation of sets using the axiom of separation with any proposition, including ones which contain quantifiers which are not bounded. Thus new sets can be formed in terms of the universe of all sets. Additionally the power set axiom implies the existence of a set of truth values. In the presence of LEM, this set exists and has two elements. In the absence of it, the set of truth values is also considered impredicative.
Myhill's constructive set theory
The subject was begun by John MyhillJohn Myhill
John R. Myhill was a mathematician, born in 1923. He received his Ph.D. from Harvard University under Willard Van Orman Quine in 1949. He was professor at SUNY Buffalo from 1966 until his death in 1987...
to provide a formal foundation for Errett Bishop
Errett Bishop
Errett Albert Bishop was an American mathematician known for his work on analysis. He is the father of constructive analysis, because of his 1967 Foundations of Constructive Analysis, where he proved most of the important theorems in real analysis by constructive methods.-Life:Errett Bishop's...
's program of constructive mathematics. As he presented it, Myhill's system CST is a constructive first-order logic with three sorts
Many-sorted logic
Many-sorted logic can reflect formally our intention, not to handle the universe as a homogeneous collection of objects, but to partition it in a way that is similar to types in typeful programming...
: natural numbers, function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s, and sets. The system is:
- Constructive first-order predicate logic with identity, and basic axioms related to the three sorts.
- The usual Peano axiomsPeano axiomsIn mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
for natural numbers. - The usual axiom of extensionalityAxiom of extensionalityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
for sets, as well as one for functions, and the usual axiom of unionAxiom of unionIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
. - A form of the axiom of infinityAxiom of infinityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
asserting that the collection of natural numbers (for which he introduces a constant N) is in fact a set. - Axioms asserting that the domainDomain (mathematics)In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
and rangeRange (mathematics)In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of a function are both sets. Additionally, an axiom of non-choice asserts the existence of a choice function in cases where the choice is already made. Together these act like the usual replacement axiomAxiom schema of replacementIn set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
in classical set theory. - The axiom of exponentiation, asserting that for any two sets, there is a third set which contains all (and only) the functions whose domain is the first set, and whose range is the second set. This is a greatly weakened form of the axiom of power setAxiom of power setIn mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
in classical set theory, to which Myhill, among others, objected on the grounds of its impredicativityImpredicativeIn mathematics and logic, impredicativity is the property of a self-referencing definition. More precisely, a definition is said to be impredicative if it invokes the set being defined, or another set which contains the thing being defined.Russell's paradox is a famous example of an impredicative...
. - The axiom of restricted, or predicative, separationAxiom schema of predicative separationIn axiomatic set theory, the axiom schema of predicative separation, or of restricted, or Δ0 separation, is a schema of axioms which is a restriction of the usual axiom schema of separation in Zermelo-Fraenkel set theory. It only asserts the existence of a subset of a set if that subset can...
, which is a weakened form of the separation axiom in classical set theory, requiring that any quantificationQuantificationQuantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
s be bounded to another set. - An axiom of dependent choiceAxiom of dependent choiceIn mathematics, the axiom of dependent choices, denoted DC, is a weak form of the axiom of choice which is still sufficient to develop most of real analysis...
, which is much weaker than the usual axiom of choice.
Aczel's constructive Zermelo–Fraenkel
Peter AczelPeter Aczel
Peter Aczel is a British mathematician, logician and computer scientist based at the University of Manchester. He is known for his work in non-well-founded set theory and constructive mathematics.-External links:*http://www.cs.man.ac.uk/~petera/...
's constructive Zermelo-Fraenkel, or CZF, is essentially IZF with its impredicative features removed. It strengthens the collection scheme, and then drops the impredicative power set axiom and replaces it with another collection scheme. Finally the separation axiom is restricted, as in Myhill's CST. This theory has a relatively simple interpretation in a version of constructive type theory and has modest proof theoretic strength as well as a fairly direct constructive and predicative justification, while retaining the language of set theory. Adding LEM to this theory also recovers full ZF.
The collection axioms are:
Strong collection schema: This is the constructive replacement for the axiom schema of replacement
Axiom schema of replacement
In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
. It states that if φ is a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
between sets which is total over a certain domain set (that is, it has at least one image of every element in the domain), then there exists a set which contains at least one image under φ of every element of the domain, and only images of elements of the domain. Formally, for any formula φ:

Subset collection schema: This is the constructive version of the power set axiom. Formally, for any formula φ:
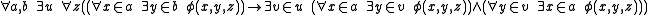
This is equivalent to a single and somewhat clearer axiom of fullness: between any two sets a and b, there is a set c which contains a total subrelation of any total relation between a and b that can be encoded as a set of ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s. Formally:
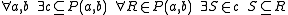
where the references to P(a,b) are defined by:


and some set-encoding of the ordered pair
The axiom of fullness implies CST's axiom of exponentiation: given two sets, the collection of all total functions from one to the other is also in fact a set.
The remaining axioms of CZF are: the axioms of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
, pairing
Axiom of pairing
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
, union
Axiom of union
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
, and infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
are the same as in ZF; and set induction
Epsilon-induction
In mathematics, \in-induction is a variant of transfinite induction, which can be used in set theory to prove that all sets satisfy a given property P[x]. If the truth of the property for x follows from its truth for all elements of x, for every set x, then the property is true of all sets...
and predicative separation
Axiom schema of predicative separation
In axiomatic set theory, the axiom schema of predicative separation, or of restricted, or Δ0 separation, is a schema of axioms which is a restriction of the usual axiom schema of separation in Zermelo-Fraenkel set theory. It only asserts the existence of a subset of a set if that subset can...
are the same as above.

