Axiom of regularity
Encyclopedia
In mathematics, the axiom of regularity (also known as the axiom of foundation) is one of the axioms of Zermelo-Fraenkel set theory and was introduced by . In first-order logic
the axiom reads: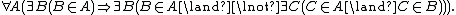
Or in prose:
Two results which follow from the axiom are that "no set is an element of itself," and that "there is no infinite sequence
(an) such that ai+1 is an element of ai for all i."
With the axiom of dependent choice
(which is a weakened form of the axiom of choice), this result can be reversed: if there are no such infinite sequences, then the axiom of regularity is true. Hence, the axiom of regularity is equivalent, given the axiom of dependent choice, to the alternative axiom that there are no downward infinite membership chains.
The axiom of regularity is arguably the least useful ingredient of Zermelo-Fraenkel set theory, since virtually all results in the branches of mathematics based on set theory hold even in the absence of regularity (see chapter 3 of ). However, it is used extensively in establishing results about well-ordering and the ordinals
in general. In addition to omitting the axiom of regularity, non-standard set theories
have indeed postulated the existence of sets that are elements of themselves.
Given the other ZF
axioms, the axiom of regularity is equivalent to the axiom of induction
.
. We see that there must be an element of {A} which is disjoint from {A}. Since the only element of {A} is A, it must be that A is disjoint from {A}. So, since A ∈ {A}, we cannot have A ∈ A (by the definition of disjoint).
, f, on the natural number
s with f(n+1) an element of f(n) for each n. Define S = {f(n): n a natural number}, the range of f, which can be seen to be a set from the axiom schema of replacement
. Applying the axiom of regularity to S, let B be an element of S which is disjoint from S. By the definition of S, B must be f(k) for some natural number k. However, we are given that f(k) contains f(k+1) which is also an element of S. So f(k+1) is in the intersection of f(k) and S. This contradicts the fact that they are disjoint sets. Since our supposition led to a contradiction, there must not be any such function, f.
The nonexistence of a set containing itself can be seen as a special case where the sequence is infinite and constant.
Notice that this argument only applies to functions f which can be represented as sets as opposed to undefinable classes. The hereditarily finite set
s, Vω, satisfy the axiom of regularity (and all other axioms of ZFC except the axiom of infinity
). So if one forms a non-trivial ultrapower
of Vω, then it will also satisfy the axiom of regularity. The resulting model will contain elements, called non-standard natural numbers, which satisfy the definition of natural numbers in that model but are not really natural numbers. They are fake natural numbers which are "larger" than any actual natural number. This model will contain infinite descending sequences of elements. For example, suppose n is a non-standard natural number, then
and 
, and 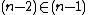so on. For any actual natural number k, 
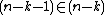. This is an unending descending sequence of elements. But this sequence is not definable in the model and thus not a set. So no contradiction to regularity can be proved.
for specifics. This definition eliminates one pair of braces from the canonical Kuratowski definition (a,b) = .
, which is entire by assumption. Thus, by the axiom of dependent choice, there is some sequence (an) in S satisfying anRan+1 for all n in N. As this is an infinite descending chain, we arrive at a contradiction and so, no such S exists.
, Russell's paradox
is the fact "the set of all sets that do not contain themselves as members" leads to a contradiction. The paradox shows that that set cannot be constructed using any consistent
set of axioms for set theory. Even though the axiom of regularity implies that no set contains itself as a member, that axiom does not banish Russell's paradox from Zermelo-Fraenkel set theory (ZF). In fact, if the ZF axioms without Regularity were already inconsistent, then adding Regularity would not make them consistent. Russell's paradox does not manifest in ZF because ZF does not prove that the proposed paradoxical set actually exists (e.g., ZF's axiom of separation only allows us to construct subset
s of some existing set, and thus cannot be used to construct the desired set). A line of reasoning similar to Russell's paradox will, in ZF, only end up proving that the collection of all sets which do not contain themselves is not a set but a proper class (actually, the class of all sets).
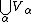(see cumulative hierarchy) is equal to the class of all sets. This statement is even equivalent to the axiom of regularity (if we work in ZF with this axiom omitted). From any model which does not satisfy axiom of regularity, a model which satisfies it can be constructed by taking only sets in 
.
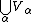First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
the axiom reads:
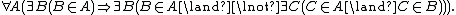
Or in prose:
- Every non-empty set A contains an element B which is disjoint from A.
Two results which follow from the axiom are that "no set is an element of itself," and that "there is no infinite sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
(an) such that ai+1 is an element of ai for all i."
With the axiom of dependent choice
Axiom of dependent choice
In mathematics, the axiom of dependent choices, denoted DC, is a weak form of the axiom of choice which is still sufficient to develop most of real analysis...
(which is a weakened form of the axiom of choice), this result can be reversed: if there are no such infinite sequences, then the axiom of regularity is true. Hence, the axiom of regularity is equivalent, given the axiom of dependent choice, to the alternative axiom that there are no downward infinite membership chains.
The axiom of regularity is arguably the least useful ingredient of Zermelo-Fraenkel set theory, since virtually all results in the branches of mathematics based on set theory hold even in the absence of regularity (see chapter 3 of ). However, it is used extensively in establishing results about well-ordering and the ordinals
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
in general. In addition to omitting the axiom of regularity, non-standard set theories
Non-well-founded set theory
Non-well-founded set theories are variants of axiomatic set theory which allow sets to contain themselves and otherwise violate the rule of well-foundedness...
have indeed postulated the existence of sets that are elements of themselves.
Given the other ZF
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
axioms, the axiom of regularity is equivalent to the axiom of induction
Epsilon-induction
In mathematics, \in-induction is a variant of transfinite induction, which can be used in set theory to prove that all sets satisfy a given property P[x]. If the truth of the property for x follows from its truth for all elements of x, for every set x, then the property is true of all sets...
.
No set is an element of itself
Let A be a set, and apply the axiom of regularity to {A}, which is a set by the axiom of pairingAxiom of pairing
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
. We see that there must be an element of {A} which is disjoint from {A}. Since the only element of {A} is A, it must be that A is disjoint from {A}. So, since A ∈ {A}, we cannot have A ∈ A (by the definition of disjoint).
No infinite descending sequence of sets exists
Suppose, to the contrary, that there is a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, f, on the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s with f(n+1) an element of f(n) for each n. Define S = {f(n): n a natural number}, the range of f, which can be seen to be a set from the axiom schema of replacement
Axiom schema of replacement
In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
. Applying the axiom of regularity to S, let B be an element of S which is disjoint from S. By the definition of S, B must be f(k) for some natural number k. However, we are given that f(k) contains f(k+1) which is also an element of S. So f(k+1) is in the intersection of f(k) and S. This contradicts the fact that they are disjoint sets. Since our supposition led to a contradiction, there must not be any such function, f.
The nonexistence of a set containing itself can be seen as a special case where the sequence is infinite and constant.
Notice that this argument only applies to functions f which can be represented as sets as opposed to undefinable classes. The hereditarily finite set
Hereditarily finite set
In mathematics and set theory, hereditarily finite sets are defined recursively as finite sets consisting of 0 or more hereditarily finite sets.-Formal definition:...
s, Vω, satisfy the axiom of regularity (and all other axioms of ZFC except the axiom of infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
). So if one forms a non-trivial ultrapower
Ultraproduct
The ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
of Vω, then it will also satisfy the axiom of regularity. The resulting model will contain elements, called non-standard natural numbers, which satisfy the definition of natural numbers in that model but are not really natural numbers. They are fake natural numbers which are "larger" than any actual natural number. This model will contain infinite descending sequences of elements. For example, suppose n is a non-standard natural number, then
and 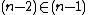, and so on. For any actual natural number k, 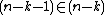. This is an unending descending sequence of elements. But this sequence is not definable in the model and thus not a set. So no contradiction to regularity can be proved.Simpler set-theoretic definition of the ordered pair
The axiom of regularity enables defining the ordered pair (a,b) as {a,{a,b}}. See ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
for specifics. This definition eliminates one pair of braces from the canonical Kuratowski definition (a,b) = .
Every set has an ordinal rank
This was actually the original form of von Neumann's axiomatization. The concept of the rank of a set had also been examined by Mirimanoff , but that work did not consider the axiom "every set has a rank" nor the consequences of such an axiom (see ).The axiom of dependent choice and no infinite descending sequence of sets implies Regularity
Let the non-empty set S be a counter-example to the axiom of regularity; that is, every element of S has a non-empty intersection with S. We define a binary relation R on S by, which is entire by assumption. Thus, by the axiom of dependent choice, there is some sequence (an) in S satisfying anRan+1 for all n in N. As this is an infinite descending chain, we arrive at a contradiction and so, no such S exists.Regularity does not resolve Russell's paradox
In naive set theoryNaive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
, Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
is the fact "the set of all sets that do not contain themselves as members" leads to a contradiction. The paradox shows that that set cannot be constructed using any consistent
Consistency proof
In logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
set of axioms for set theory. Even though the axiom of regularity implies that no set contains itself as a member, that axiom does not banish Russell's paradox from Zermelo-Fraenkel set theory (ZF). In fact, if the ZF axioms without Regularity were already inconsistent, then adding Regularity would not make them consistent. Russell's paradox does not manifest in ZF because ZF does not prove that the proposed paradoxical set actually exists (e.g., ZF's axiom of separation only allows us to construct subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of some existing set, and thus cannot be used to construct the desired set). A line of reasoning similar to Russell's paradox will, in ZF, only end up proving that the collection of all sets which do not contain themselves is not a set but a proper class (actually, the class of all sets).
Regularity and cumulative hierarchy
In ZF it can be proven that the class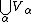 (see cumulative hierarchy) is equal to the class of all sets. This statement is even equivalent to the axiom of regularity (if we work in ZF with this axiom omitted). From any model which does not satisfy axiom of regularity, a model which satisfies it can be constructed by taking only sets in 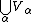.External links
- http://www.trinity.edu/cbrown/topics_in_logic/sets/sets.html contains an informative description of the axiom of regularity under the section on Zermelo-Fraenkel set theory.