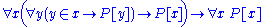Epsilon-induction
Encyclopedia
In mathematics
,
-induction (epsilon-induction) is a variant of transfinite induction
, which can be used in set theory to prove that all sets satisfy a given property P[x]. If the truth of the property for x follows from its truth for all elements of x, for every set x, then the property is true of all sets. In symbols:
This principle, sometimes called the axiom of induction (in set theory), is equivalent to the axiom of regularity
.
-induction is a special case of well-founded induction.
The name is most often pronounced "epsilon-induction", because the set membership symbol
historically developed from the Greek letter 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
,
-induction (epsilon-induction) is a variant of transfinite inductionTransfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
, which can be used in set theory to prove that all sets satisfy a given property P[x]. If the truth of the property for x follows from its truth for all elements of x, for every set x, then the property is true of all sets. In symbols:
This principle, sometimes called the axiom of induction (in set theory), is equivalent to the axiom of regularity
Axiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
.
-induction is a special case of well-founded induction.The name is most often pronounced "epsilon-induction", because the set membership symbol
historically developed from the Greek letter .