
Erdős–Rado theorem
Encyclopedia
In partition calculus, part of combinatorial set theory, which is a branch of mathematics, the Erdős–Rado theorem is a basic result, extending Ramsey's theorem
to uncountable sets.
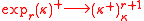
where exp0(κ)=κ and inductively expr+1(κ)=2expr(κ). This is sharp in the sense that expr(κ)+ cannot be replaced by expr(κ) on the left hand side.
The above partition symbol describes the following statement. If f is a coloring of the r+1-element subsets of a set of cardinality expr(κ)+, then there is a homogeneous set of cardinality κ+ (a set, all whose r+1-element subsets get the same f-value).
Ramsey's theorem
In combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
to uncountable sets.
Statement of the theorem
If r≥2 is finite, κ is an infinite cardinal, then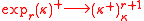
where exp0(κ)=κ and inductively expr+1(κ)=2expr(κ). This is sharp in the sense that expr(κ)+ cannot be replaced by expr(κ) on the left hand side.
The above partition symbol describes the following statement. If f is a coloring of the r+1-element subsets of a set of cardinality expr(κ)+, then there is a homogeneous set of cardinality κ+ (a set, all whose r+1-element subsets get the same f-value).

