Constructible universe
Encyclopedia
In mathematics
, the constructible universe (or Gödel's constructible universe), denoted L, is a particular class
of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel
in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis". In this, he proved that the constructible universe is an inner model
of ZF
set theory
, and also that the axiom of choice and the generalized continuum hypothesis are true in the constructible universe. This shows that both propositions are consistent with the basic axiom
s of set theory, if ZF itself is consistent. Since many other theorems only hold in systems in which one or both of the propositions is true, their consistency is an important result.
, V. The stages are indexed by ordinals
. In von Neumann's universe, at a successor
stage, one takes Vα+1 to be the set of ALL subsets of the previous stage, Vα. By contrast, in Gödel's constructible universe L, one uses only those subsets of the previous stage that are:
By limiting oneself to sets defined only in terms of what has already been constructed, one ensures that the resulting sets will be constructed in a way that is independent of the peculiarities of the surrounding model of set theory and contained in any such model.
Define
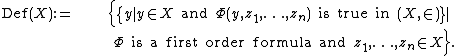
L is defined by transfinite recursion as follows:
If z is an element of Lα, then z = {y | y ∈ Lα and y ∈ z} ∈ Def (Lα) = Lα+1. So Lα is a subset of Lα+1 which is a subset of the power set of Lα. Consequently, this is a tower of nested transitive set
s. But L itself is a proper class.
The elements of L are called "constructible" sets; and L itself is the "constructible universe". The "axiom of constructibility
", aka "V=L", says that every set (of V) is constructible, i.e. in L.
For any finite ordinal n, the sets Ln and Vn are the same (whether V equals L or not), and thus Lω = Vω: their elements are exactly the hereditarily finite set
s. Equality beyond this point does not hold. Even in models of ZFC
in which V equals L, Lω+1 is a proper subset of Vω+1, and thereafter Lα+1 is a proper subset of the powerset of Lα for all α > ω.
If α is an infinite ordinal then there is a bijection between Lα and α, and the bijection is constructible. So these sets are equinumerous in any model of set theory which includes them.
As defined above, Def(X) is the set of subsets of X defined by Δ0 formulas (that is, formulas of set theory which contain only bounded quantifiers) which use as parameters only X and its elements.
An alternate definition, due to Gödel, characterizes each Lα+1 as the intersection of the powerset of Lα with the closure of
under a collection of nine explicit functions. This definition makes no reference to definability.
All arithmetical
subsets of ω and relations on ω belong to Lω+1 (because the arithmetic definition gives one in Lω+1). Conversely, any subset of ω belonging to Lω+1 is arithmetical (because elements of Lω can be coded by natural numbers in such a way that ∈ is definable, i.e., arithmetic). On the other hand, Lω+2 already contains certain non-arithmetical subsets of ω, such as the set of (natural numbers coding) true arithmetical statements (this can be defined from Lω+1 so it is in Lω+2).
All hyperarithmetical subsets of ω and relations on ω belong to
(where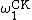 
stands for the Church-Kleene ordinal), and conversely any subset of ω which belongs to 
is hyperarithmetical.
, which means that it satisfies the following axiom
s:
Notice that the proof that L is a model of ZFC only requires that V be a model of ZF, i.e. we do NOT assume that the axiom of choice holds in V.
Furthermore, since L is a subclass of V and, similarly, L is a subclass of W, L is the smallest class containing all the ordinals which is a standard model of ZF. Indeed, L is the intersection of all such classes.
If there is a set W in V which is a standard model
of ZF, and the ordinal κ is the set of ordinals which occur in W, then Lκ is the L of W. If there is a set which is a standard model of ZF, then the smallest such set is such a Lκ. This set is called the minimal model
of ZFC. Using the downward Löwenheim–Skolem theorem
, one can show that the minimal model (if it exists) is a countable set.
Of course, any consistent theory must have a model, so even within the minimal model of set theory there are sets which are models of ZF (assuming ZF is consistent). However, those set models are non-standard. In particular, they do not use the normal element relation and they are not well founded.
Because both the L of L and the V of L are the real L and both the L of Lκ and the V of Lκ are the real Lκ, we get that V=L is true in L and in any Lκ which is a model of ZF. However, V=L does not hold in any other standard model of ZF.
s become strongly inaccessible. Weakly Mahlo cardinal
s become strongly Mahlo. And more generally, any large cardinal property weaker than 0#
(see the list of large cardinal properties) will be retained in L.
However, 0# is false in L even if true in V. So all the large cardinals whose existence implies 0# cease to have those large cardinal properties, but retain the properties weaker than 0# which they also possess. For example, measurable cardinal
s cease to be measurable but remain Mahlo in L.
Interestingly, if 0# holds in V, then there is a closed unbounded class
of ordinals which are indiscernible in L. While some of these are not even initial ordinals in V, they have all the large cardinal properties weaker than 0# in L. Furthermore, any strictly increasing class function from the class of indiscernibles to itself can be extended in a unique way to an elementary embedding of L into L. This gives L a nice structure of repeating segments.
Suppose x and y are two different sets in L and we wish to determine whether xy. If x first appears in Lα+1 and y first appears in Lβ+1 and β is different from α, then let x
Remember that Lα+1 = Def (Lα) which uses formulas with parameters from Lα to define the sets x and y. If one discounts (for the moment) the parameters, the formulas can be given a standard Gödel numbering by the natural numbers. If Φ is the formula with the smallest Gödel number which can be used to define x and Ψ is the formula with the smallest Gödel number which can be used to define y and Ψ is different from Φ, then let x
Suppose that Φ uses n parameters from Lα. Suppose z1,...,zn is the sequence of parameters least in the reverse-lexicographic ordering which can be used with Φ to define x and w1,...,wn does same for y. Then let xnn or (zn=wn and zn-1n-1) or (zn=wn and zn-1=wn-1 and zn-2n-2) or etc.. It being understood that each parameter's possible values are ordered according to the restriction of the ordering of L to Lα, so this definition involves transfinite recursion on α.
The well-ordering of the values of single parameters is provided by the inductive hypothesis of the transfinite induction. The values of n-tuples of parameters are well-ordered by the product ordering. The formulas with parameters are well-ordered by the ordered sum (by Gödel numbers) of well-orderings. And L is well-ordered by the ordered sum (indexed by α) of the orderings on Lα+1.
Notice that this well-ordering can be defined within L itself by a formula of set theory with no parameters, only the free-variables x and y. And this formula gives the same truth value regardless of whether it is evaluated in L, V, or W (some other standard model of ZF with the same ordinals) and we will suppose that the formula is false if either x or y is not in L.
It is well known that the axiom of choice is equivalent to the ability to well-order every set. Being able to well-order the proper class V (as we have done here with L) is equivalent to the axiom of global choice
which is more powerful than the ordinary axiom of choice because it also covers proper classes of non-empty sets.
for L. Here we describe such a principle.
By mathematical induction on n<ω, we can use ZF in V to prove that for any ordinal α, there is an ordinal β>α such that for any sentence P(z1,...,zk) with z1,...,zk in Lβ and containing fewer than n symbols (counting a constant symbol for an element of Lβ as one symbol) we get that P(z1,...,zk) holds in Lβ if and only if it holds in L.
Φ(...) to X. Notice that each zk∈Lβ+1 for some β<α. Combine formulas for the z's with the formula for s and apply existential quantifiers over the z's outside and one gets a formula which defines the constructible set s using only the ordinals α which appear in expressions like X=Lα as parameters.
Example: The set {5,ω} is constructible. It is the unique set, s, which satisfies the formula:
,
where
is short for:
Actually, even this complex formula has been simplified from what the instructions given in the first paragraph would yield. But the point remains, there is a formula of set theory which is true only for the desired constructible set s and which contains parameters only for ordinals.
The class L(A) for a non-constructible set A is the intersection of all classes which are standard models of set theory and contain A and all the ordinals.
L(A) is defined by transfinite recursion as follows:
If L(A) contains a well-ordering of the transitive closure of {A}, then this can be extended to a well-ordering of L(A). Otherwise, the axiom of choice will fail in L(A).
A common example is L(R), the smallest model which contains all the real numbers, which is used extensively in modern descriptive set theory
.
The class L[A] is the class of sets whose construction is influenced by A, where A may be a (presumably non-constructible) set or a proper class. The definition of this class uses DefA (X), which is the same as Def (X) except instead of evaluating the truth of formulas Φ in the model (X,∈), one uses the model (X,∈,A) where A is a unary predicate. The intended interpretation of A(y) is y∈A. Then the definition of L[A] is exactly that of L only with Def replaced by DefA.
L[A] is always a model of the axiom of choice. Even if A is a set, A is not necessarily itself a member of L[A], although it always is if A is a set of ordinals.
It is essential to remember that the sets in L(A) or L[A] are usually not actually constructible and that the properties of these models may be quite different from the properties of L itself.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the constructible universe (or Gödel's constructible universe), denoted L, is a particular class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis". In this, he proved that the constructible universe is an inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
of ZF
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, and also that the axiom of choice and the generalized continuum hypothesis are true in the constructible universe. This shows that both propositions are consistent with the basic axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s of set theory, if ZF itself is consistent. Since many other theorems only hold in systems in which one or both of the propositions is true, their consistency is an important result.
What is L?
L can be thought of as being built in "stages" resembling the von Neumann universeVon Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
, V. The stages are indexed by ordinals
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
. In von Neumann's universe, at a successor
Successor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
stage, one takes Vα+1 to be the set of ALL subsets of the previous stage, Vα. By contrast, in Gödel's constructible universe L, one uses only those subsets of the previous stage that are:
- definable by a formula in the formal languageFormal languageA formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
of set theory - with parameters from the previous stage and
- with the quantifiersQuantificationQuantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
interpreted to range over the previous stage.
By limiting oneself to sets defined only in terms of what has already been constructed, one ensures that the resulting sets will be constructed in a way that is independent of the peculiarities of the surrounding model of set theory and contained in any such model.
Define
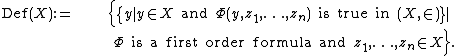
L is defined by transfinite recursion as follows:
-
-
- If
is a limit ordinal, then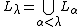 
. -
.
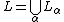If z is an element of Lα, then z = {y | y ∈ Lα and y ∈ z} ∈ Def (Lα) = Lα+1. So Lα is a subset of Lα+1 which is a subset of the power set of Lα. Consequently, this is a tower of nested transitive set
Transitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
s. But L itself is a proper class.
The elements of L are called "constructible" sets; and L itself is the "constructible universe". The "axiom of constructibility
Axiom of constructibility
The axiom of constructibility is a possible axiom for set theory in mathematics that asserts that every set is constructible. The axiom is usually written as V = L, where V and L denote the von Neumann universe and the constructible universe, respectively.- Implications :The axiom of...
", aka "V=L", says that every set (of V) is constructible, i.e. in L.
Additional facts about the sets Lα
An equivalent definition for Lα is:-
- For any ordinal α,
.
- For any ordinal α,
For any finite ordinal n, the sets Ln and Vn are the same (whether V equals L or not), and thus Lω = Vω: their elements are exactly the hereditarily finite set
Hereditarily finite set
In mathematics and set theory, hereditarily finite sets are defined recursively as finite sets consisting of 0 or more hereditarily finite sets.-Formal definition:...
s. Equality beyond this point does not hold. Even in models of ZFC
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
in which V equals L, Lω+1 is a proper subset of Vω+1, and thereafter Lα+1 is a proper subset of the powerset of Lα for all α > ω.
If α is an infinite ordinal then there is a bijection between Lα and α, and the bijection is constructible. So these sets are equinumerous in any model of set theory which includes them.
As defined above, Def(X) is the set of subsets of X defined by Δ0 formulas (that is, formulas of set theory which contain only bounded quantifiers) which use as parameters only X and its elements.
An alternate definition, due to Gödel, characterizes each Lα+1 as the intersection of the powerset of Lα with the closure of
under a collection of nine explicit functions. This definition makes no reference to definability.All arithmetical
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
subsets of ω and relations on ω belong to Lω+1 (because the arithmetic definition gives one in Lω+1). Conversely, any subset of ω belonging to Lω+1 is arithmetical (because elements of Lω can be coded by natural numbers in such a way that ∈ is definable, i.e., arithmetic). On the other hand, Lω+2 already contains certain non-arithmetical subsets of ω, such as the set of (natural numbers coding) true arithmetical statements (this can be defined from Lω+1 so it is in Lω+2).
All hyperarithmetical subsets of ω and relations on ω belong to
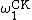(where stands for the Church-Kleene ordinal), and conversely any subset of ω which belongs to is hyperarithmetical.L is a standard inner model of ZFC
L is a standard model, i.e. it is a transitive class and it uses the real element relationship, so it is well-founded. L is an inner model, i.e. it contains all the ordinal numbers of V and it has no "extra" sets beyond those in V, but it might be a proper subclass of V. L is a model of ZFCZermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, which means that it satisfies the following axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s:
- Axiom of regularityAxiom of regularityIn mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
: Every non-empty set x contains some element y such that x and y are disjoint sets. is a substructure of (V,∈) which is well founded, so L is well founded. In particular, if x∈L, then by the transitivity of L, y∈L. If we use this same y as in V, then it is still disjoint from x because we are using the same element relation and no new sets were added. - Axiom of extensionalityAxiom of extensionalityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
: Two sets are the same if and only if they have the same elements.
- If x and y are in L and they have the same elements in L, then by L's transitivity, they have the same elements (in V). So they are equal (in V and thus in L).
- Axiom of empty setAxiom of empty setIn axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
: {} is a set.
- Axiom of empty set
- {} = L0 = {y|y∈L0 and y=y} ∈ L1. So {} ∈ L. Since the element relation is the same and no new elements were added, this is the empty set of L.
- Axiom of pairingAxiom of pairingIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
: If x, y are sets, then {x,y} is a set.
- Axiom of pairing
- If x∈L and y∈L, then there is some ordinal α such that x∈Lα and y∈Lα. Then {x,y} = {s|s∈Lα and (s=x or s=y)} ∈ Lα+1. Thus {x,y} ∈ L and it has the same meaning for L as for V.
- Axiom of unionAxiom of unionIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
: For any set x there is a set y whose elements are precisely the elements of the elements of x.
- Axiom of union
- If x ∈ Lα, then its elements are in Lα and their elements are also in Lα. So y is a subset of Lα. y = {s|s∈Lα and there exists z∈x such that s∈z} ∈ Lα+1. Thus y ∈ L.
- Axiom of infinityAxiom of infinityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
: There exists a set x such that {} is in x and whenever y is in x, so is the union y U {y}.
- Axiom of infinity
- From transfinite induction, we get that each ordinal α ∈ Lα+1. In particular, ω ∈ Lω+1 and thus ω ∈ L.
- Axiom of separation: Given any set S and any proposition P(x,z1,...,zn), {x|x∈S and P(x,z1,...,zn)} is a set.
- By induction on subformulas of P, one can show that there is an α such that Lα contains S and z1,...,zn and (P is true in Lα if and only if P is true in L (this is called the "reflection principleReflection principleIn set theory, a branch of mathematics, a reflection principle says that it is possible to find sets that resemble the class of all sets. There are several different forms of the reflection principle depending on exactly what is meant by "resemble"...
")). So {x|x∈S and P(x,z1,...,zn) holds in L} = {x|x∈Lα and x∈S and P(x,z1,...,zn) holds in Lα} ∈ Lα+1. Thus the subset is in L.- Axiom of replacement: Given any set S and any mapping (formally defined as a proposition P(x,y) where P(x,y) and P(x,z) implies y = z), {y | there exists x∈S such that P(x,y)} is a set.
- Let Q(x,y) be the formula which relativizes P to L, i.e. all quantifiers in P are restricted to L. Q is a much more complex formula than P, but it is still a finite formula; and we can apply replacement in V to Q. So {y|y∈L and there exists x∈S such that P(x,y) holds in L} = {y | there exists x∈S such that Q(x,y)} is a set in V and a subclass of L. Again using the axiom of replacement in V, we can show that there must be an α such that this set is a subset of Lα ∈ Lα+1. Then one can use the axiom of separation in L to finish showing that it is an element of L.
- Axiom of power setAxiom of power setIn mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
: For any set x there exists a set y, such that the elements of y are precisely the subsets of x.
- Axiom of power set
- In general, some subsets of a set in L will not be in L. So the whole power set of a set in L will usually not be in L. What we need here is to show that the intersection of the power set with L is in L. Use replacement in V to show that there is an α such that the intersection is a subset of Lα. Then the intersection is {z|z∈Lα and z is a subset of x} ∈ Lα+1. Thus the required set is in L.
- Axiom of choice: Given a set x of mutually disjoint nonempty sets, there is a set y (a choice set for x) containing exactly one element from each member of x.
- One can show that there is a definable well-ordering of L which definition works the same way in L itself. So one chooses the least element of each member of x to form y using the axioms of union and separation in L.
Notice that the proof that L is a model of ZFC only requires that V be a model of ZF, i.e. we do NOT assume that the axiom of choice holds in V.
L is absolute and minimal
If W is any standard model of ZF sharing the same ordinals as V, then the L defined in W is the same as the L defined in V. In particular, Lα is the same in W and V, for any ordinal α. And the same formulas and parameters in Def (Lα) produce the same constructible sets in Lα+1.Furthermore, since L is a subclass of V and, similarly, L is a subclass of W, L is the smallest class containing all the ordinals which is a standard model of ZF. Indeed, L is the intersection of all such classes.
If there is a set W in V which is a standard model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
of ZF, and the ordinal κ is the set of ordinals which occur in W, then Lκ is the L of W. If there is a set which is a standard model of ZF, then the smallest such set is such a Lκ. This set is called the minimal model
Minimal model (set theory)
In set theory, a minimal model is a minimal standard model of ZFC.Minimal models were introduced by .The existence of a minimal model cannot be proved in ZFC, even assuming that ZFC is consistent, but follows from the existence of a standard model as follows...
of ZFC. Using the downward Löwenheim–Skolem theorem
Löwenheim–Skolem theorem
In mathematical logic, the Löwenheim–Skolem theorem, named for Leopold Löwenheim and Thoralf Skolem, states that if a countable first-order theory has an infinite model, then for every infinite cardinal number κ it has a model of size κ...
, one can show that the minimal model (if it exists) is a countable set.
Of course, any consistent theory must have a model, so even within the minimal model of set theory there are sets which are models of ZF (assuming ZF is consistent). However, those set models are non-standard. In particular, they do not use the normal element relation and they are not well founded.
Because both the L of L and the V of L are the real L and both the L of Lκ and the V of Lκ are the real Lκ, we get that V=L is true in L and in any Lκ which is a model of ZF. However, V=L does not hold in any other standard model of ZF.
L and large cardinals
Since On⊂L⊆V, properties of ordinals which depend on the absence of a function or other structure (i.e. Π1ZF formulas) are preserved when going down from V to L. Hence initial ordinals of cardinals remain initial in L. Regular ordinals remain regular in L. Weak limit cardinals become strong limit cardinals in L because the generalized continuum hypothesis holds in L. Weakly inaccessible cardinalInaccessible cardinal
In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
s become strongly inaccessible. Weakly Mahlo cardinal
Mahlo cardinal
In mathematics, a Mahlo cardinal is a certain kind of large cardinal number. Mahlo cardinals were first described by . As with all large cardinals, none of these varieties of Mahlo cardinals can be proved to exist by ZFC ....
s become strongly Mahlo. And more generally, any large cardinal property weaker than 0#
Zero sharp
In the mathematical discipline of set theory, 0# is the set of true formulas about indiscernibles in the Gödel constructible universe. It is often encoded as a subset of the integers , or as a subset of the hereditarily finite sets, or as a real number...
(see the list of large cardinal properties) will be retained in L.
However, 0# is false in L even if true in V. So all the large cardinals whose existence implies 0# cease to have those large cardinal properties, but retain the properties weaker than 0# which they also possess. For example, measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
s cease to be measurable but remain Mahlo in L.
Interestingly, if 0# holds in V, then there is a closed unbounded class
Club set
In mathematics, particularly in mathematical logic and set theory, a club set is a subset of a limit ordinal which is closed under the order topology, and is unbounded relative to the limit ordinal...
of ordinals which are indiscernible in L. While some of these are not even initial ordinals in V, they have all the large cardinal properties weaker than 0# in L. Furthermore, any strictly increasing class function from the class of indiscernibles to itself can be extended in a unique way to an elementary embedding of L into L. This gives L a nice structure of repeating segments.
L can be well-ordered
There are various ways of well-ordering L. Some of these involve the "fine structure" of L which was first described by Ronald Bjorn Jensen in his 1972 paper entitled "The fine structure of the constructible hierarchy". Instead of explaining the fine structure, we will give an outline of how L could be well-ordered using only the definition given above.Suppose x and y are two different sets in L and we wish to determine whether x
Remember that Lα+1 = Def (Lα) which uses formulas with parameters from Lα to define the sets x and y. If one discounts (for the moment) the parameters, the formulas can be given a standard Gödel numbering by the natural numbers. If Φ is the formula with the smallest Gödel number which can be used to define x and Ψ is the formula with the smallest Gödel number which can be used to define y and Ψ is different from Φ, then let x
Suppose that Φ uses n parameters from Lα. Suppose z1,...,zn is the sequence of parameters least in the reverse-lexicographic ordering which can be used with Φ to define x and w1,...,wn does same for y. Then let x
The well-ordering of the values of single parameters is provided by the inductive hypothesis of the transfinite induction. The values of n-tuples of parameters are well-ordered by the product ordering. The formulas with parameters are well-ordered by the ordered sum (by Gödel numbers) of well-orderings. And L is well-ordered by the ordered sum (indexed by α) of the orderings on Lα+1.
Notice that this well-ordering can be defined within L itself by a formula of set theory with no parameters, only the free-variables x and y. And this formula gives the same truth value regardless of whether it is evaluated in L, V, or W (some other standard model of ZF with the same ordinals) and we will suppose that the formula is false if either x or y is not in L.
It is well known that the axiom of choice is equivalent to the ability to well-order every set. Being able to well-order the proper class V (as we have done here with L) is equivalent to the axiom of global choice
Axiom of global choice
In class theories, the axiom of global choice is a stronger variant of the axiom of choice which applies to proper classes as well as sets.- Statement :The axiom can be expressed in various ways which are equivalent:...
which is more powerful than the ordinary axiom of choice because it also covers proper classes of non-empty sets.
L has a reflection principle
Proving that the axiom of separation, axiom of replacement, and axiom of choice hold in L requires (at least as shown above) the use of a reflection principleReflection principle
In set theory, a branch of mathematics, a reflection principle says that it is possible to find sets that resemble the class of all sets. There are several different forms of the reflection principle depending on exactly what is meant by "resemble"...
for L. Here we describe such a principle.
By mathematical induction on n<ω, we can use ZF in V to prove that for any ordinal α, there is an ordinal β>α such that for any sentence P(z1,...,zk) with z1,...,zk in Lβ and containing fewer than n symbols (counting a constant symbol for an element of Lβ as one symbol) we get that P(z1,...,zk) holds in Lβ if and only if it holds in L.
Constructible sets are definable from the ordinals
There is a formula of set theory which expresses the idea that X=Lα. It has only free variables for X and α. Using this we can expand the definition of each constructible set. If s∈Lα+1, then s = {y|y∈Lα and Φ(y,z1,...,zn) holds in (Lα,∈)} for some formula Φ and some z1,...,zn in Lα. This is equivalent to saying that: for all y, y∈s if and only if [there exists X such that X=Lα and y∈X and Ψ(X,y,z1,...,zn)] where Ψ(X,...) is the result of restricting each quantifier inΦ(...) to X. Notice that each zk∈Lβ+1 for some β<α. Combine formulas for the z's with the formula for s and apply existential quantifiers over the z's outside and one gets a formula which defines the constructible set s using only the ordinals α which appear in expressions like X=Lα as parameters.
Example: The set {5,ω} is constructible. It is the unique set, s, which satisfies the formula:
,where
is short for:Actually, even this complex formula has been simplified from what the instructions given in the first paragraph would yield. But the point remains, there is a formula of set theory which is true only for the desired constructible set s and which contains parameters only for ordinals.
Relative constructibility
Sometimes it is desirable to find a model of set theory which is narrow like L, but which includes or is influenced by a set which is not constructible. This gives rise to the concept of relative constructibility, of which there are two flavors, denoted L(A) and L[A].The class L(A) for a non-constructible set A is the intersection of all classes which are standard models of set theory and contain A and all the ordinals.
L(A) is defined by transfinite recursion as follows:
- L0(A) = the smallest transitive set containing A as an element, i.e. the transitive closure of {A}.
- Lα+1(A) = Def (Lα(A))
- If λ is a limit ordinal, then
. 
.
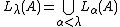If L(A) contains a well-ordering of the transitive closure of {A}, then this can be extended to a well-ordering of L(A). Otherwise, the axiom of choice will fail in L(A).
A common example is L(R), the smallest model which contains all the real numbers, which is used extensively in modern descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
.
The class L[A] is the class of sets whose construction is influenced by A, where A may be a (presumably non-constructible) set or a proper class. The definition of this class uses DefA (X), which is the same as Def (X) except instead of evaluating the truth of formulas Φ in the model (X,∈), one uses the model (X,∈,A) where A is a unary predicate. The intended interpretation of A(y) is y∈A. Then the definition of L[A] is exactly that of L only with Def replaced by DefA.
L[A] is always a model of the axiom of choice. Even if A is a set, A is not necessarily itself a member of L[A], although it always is if A is a set of ordinals.
It is essential to remember that the sets in L(A) or L[A] are usually not actually constructible and that the properties of these models may be quite different from the properties of L itself.
See also
- Axiom of constructibilityAxiom of constructibilityThe axiom of constructibility is a possible axiom for set theory in mathematics that asserts that every set is constructible. The axiom is usually written as V = L, where V and L denote the von Neumann universe and the constructible universe, respectively.- Implications :The axiom of...
- Statements true in LStatements true in LHere is a list of propositions that hold in the constructible universe :* The generalized continuum hypothesis and as a consequence** The axiom of choice* Diamondsuit** Clubsuit* Global square* The existence of morasses...
- Reflection principleReflection principleIn set theory, a branch of mathematics, a reflection principle says that it is possible to find sets that resemble the class of all sets. There are several different forms of the reflection principle depending on exactly what is meant by "resemble"...
- Axiomatic set theory
- Transitive setTransitive setIn set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
- L(R)L(R)In set theory, L is the smallest transitive inner model of ZF containing all the ordinals and all the reals. It can be constructed in a manner analogous to the construction of L , by adding in all the reals at the start, and then iterating the definable powerset operation through all the...
- Ordinal definable