
Transitive set
Encyclopedia
In set theory
, a set A is transitive, if
Similarly, a class
M is transitive if every element of M is a subset of M.
s suggested by John von Neumann
, ordinal numbers are defined as hereditarily
transitive sets: an ordinal number is a transitive set whose members are also transitive (and thus ordinals).
Any of the stages Vα and Lα leading to the construction of the von Neumann universe
V and Gödel's constructible universe L are transitive sets. The universe
s L and V themselves are transitive classes.
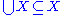 , where
, where 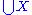 is the union
is the union
of all elements of X that are sets, . If X is transitive, then
. If X is transitive, then 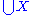 is transitive. If X and Y are transitive, then X∪Y∪{X,Y} is transitive. In general, if X is a class all of whose elements are transitive sets, then
is transitive. If X and Y are transitive, then X∪Y∪{X,Y} is transitive. In general, if X is a class all of whose elements are transitive sets, then 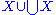 is transitive.
is transitive.
A set X which does not contain urelements is transitive if and only if it is a subset of its own power set,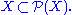 The power set of a transitive set without urelements is transitive.
The power set of a transitive set without urelements is transitive.

Note that this is the set of all of the objects related to X by the transitive closure
of the membership relation.
s. The reason is that properties defined by bounded formulas
are absolute
for transitive classes.
A transitive set (or class) that is a model of a formal system
of set theory is called a transitive model of the system. Transitivity is an important factor in determining the absoluteness of formulas.
In the superstructure approach to non-standard analysis
, the non-standard universes satisfy strong transitivity, see (Goldblatt, 1998, p.161).
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a set A is transitive, if
- whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,
- whenever x ∈ A, and x is not an urelement, then x is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of A.
Similarly, a class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
M is transitive if every element of M is a subset of M.
Examples
Using the definition of ordinal numberOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s suggested by John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, ordinal numbers are defined as hereditarily
Hereditary property
In mathematics, a hereditary property is a property of an object, that inherits to all its subobjects, where the term subobject depends on the context. These properties are particularly considered in topology and graph theory.-In topology:...
transitive sets: an ordinal number is a transitive set whose members are also transitive (and thus ordinals).
Any of the stages Vα and Lα leading to the construction of the von Neumann universe
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
V and Gödel's constructible universe L are transitive sets. The universe
Universe (mathematics)
In mathematics, and particularly in set theory and the foundations of mathematics, a universe is a class that contains all the entities one wishes to consider in a given situation...
s L and V themselves are transitive classes.
Properties
A set X is transitive if and only if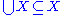 , where
, where 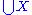 is the union
is the unionUnion (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of all elements of X that are sets,
 . If X is transitive, then
. If X is transitive, then 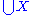 is transitive. If X and Y are transitive, then X∪Y∪{X,Y} is transitive. In general, if X is a class all of whose elements are transitive sets, then
is transitive. If X and Y are transitive, then X∪Y∪{X,Y} is transitive. In general, if X is a class all of whose elements are transitive sets, then 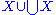 is transitive.
is transitive.A set X which does not contain urelements is transitive if and only if it is a subset of its own power set,
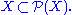 The power set of a transitive set without urelements is transitive.
The power set of a transitive set without urelements is transitive.Transitive closure
The transitive closure of a set X is the smallest (with respect to inclusion) transitive set which contains X. Suppose one is given a set X, then the transitive closure of X is
Note that this is the set of all of the objects related to X by the transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of the membership relation.
Transitive models of set theory
Transitive classes are often used for construction of interpretations of set theory in itself, usually called inner modelInner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
s. The reason is that properties defined by bounded formulas
Bounded quantifier
In the study of formal theories in mathematical logic, bounded quantifiers are often added to a language in addition to the standard quantifiers "∀" and "∃". Bounded quantifiers differ from "∀" and "∃" in that bounded quantifiers restrict the range of the quantified variable...
are absolute
Absoluteness (mathematical logic)
In mathematical logic, a formula is said to be absolute if it has the same truth value in each of some class of structures . Theorems about absoluteness typically establish relationships between the absoluteness of formulas and their syntactic form.There are two weaker forms of partial absoluteness...
for transitive classes.
A transitive set (or class) that is a model of a formal system
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
of set theory is called a transitive model of the system. Transitivity is an important factor in determining the absoluteness of formulas.
In the superstructure approach to non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
, the non-standard universes satisfy strong transitivity, see (Goldblatt, 1998, p.161).

