Zermelo set theory
Encyclopedia
Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo
, is the ancestor of modern set theory
. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted. This article sets out the original axioms, with the original text (translated into English) and original numbering.
The axioms do not include the Axiom of regularity
and Axiom of replacement. These were added as the result of work by Thoralf Skolem
in 1922, based on earlier work by Abraham Fraenkel in the same year.
In the modern ZFC system, the "propositional function" referred to in the axiom of separation is interpreted as "any property definable by a first order formula with parameters", so the separation axiom is replaced by an axiom scheme. The notion of "first order formula" was not known in 1904 when Zermelo published his axiom system, and he later rejected this interpretation as being too restrictive. Zermelo set theory is usually taken to be a first-order theory with the separation axiom replaced by an axiom scheme with an axiom for each first-order formula. It can also be considered as a theory in second-order logic
, where now the separation axiom is just a single axiom. The second-order interpretation of Zermelo set theory is probably closer to Zermelo's own conception of it, and is stronger than the first-order interpretation.
In the usual cumulative hierarchy
Vα of ZFC set theory (for ordinals α), any one of the sets
Vα for α a limit ordinal larger than the first infinite ordinal ω (such as Vω·2) forms a model of Zermelo set theory. So the consistency of Zermelo set theory is a theorem of ZFC set theory. Zermelo's axioms do not imply the existence of ℵω or larger infinite cardinals, as the model Vω·2 does not contain such cardinals. (Cardinals have to be defined differently in Zermelo set theory, as the usual definition of cardinals and ordinals does not work very well: with the usual definition it is not even possible to prove the existence of the ordinal ω2.)
The axiom of infinity
is usually now modified to assert the existence of the first infinite
von Neumann ordinal
; the original Zermelo
axioms cannot prove the existence of this set, nor can the modified Zermelo axioms prove Zermelo's
axiom of infinity. Zermelo's axioms (original or modified) cannot prove the existence of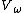
as a set nor of any rank of the cumulative hierarchy of sets with infinite index.
Zermelo set theory is similar in strength to topos theory with a natural number object
, or to the system in Principia mathematica
. It is strong enough to carry out almost all ordinary mathematics not directly connected with set theory or logic.
".
He says he wants to show how the original theory of Georg Cantor
and Richard Dedekind
can be reduced to a few definitions and seven principles or axioms. He says he has not been able to prove that the axioms are consistent.
A non-constructivist argument for their consistency goes as follows. Define Vα for α one of the ordinals 0, 1, 2, ...,ω, ω+1, ω+2,..., ω·2 as follows:
Then the axioms of Zermelo set theory are consistent because they are true in the model Vω·2. While a non-constructivist might regard this as a valid argument, a constructivist would probably not: while there are no problems with the construction of the sets up to Vω, the construction of Vω+1 is less clear because one cannot constructively define every subset of Vω. This argument can be turned into a valid proof in Zermelo-Frenkel set theory, but this does not really help because the consistency of Zermelo-Frenkel set theory is less clear than the consistency of Zermelo set theory.
Sets cannot be independently defined by any arbitrary logically definable notion. They must be constructed in some way from previously constructed sets. For example they can be constructed by taking powersets, or they can be separated as subsets of sets already "given". This, he says, eliminates contradictory ideas like "the set of all sets" or "the set of all ordinal numbers".
He disposes of the Russell paradox by means of this Theorem: "Every set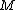
possesses at least one subset 
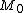that is not an element of 
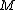". Let 
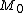be the subset of 
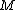for which, by AXIOM III, is separated out by the notion "
". Then 
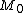cannot be in 
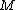. For
Therefore the assumption that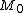
is in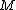 
is wrong, proving the theorem. Hence not all objects of the universal domain B can be elements of one and the same set. "This disposes of the Russell antinomy
as far as we are concerned".
This left the problem of "the domain B" which seems to refer to something. This led to the idea of a proper class.
explicitly and by name. This appeals strictly to set theoretical notions, and is thus not exactly the same as Cantor's diagonal argument
.
Cantor's theorem: "If M is an arbitrary set, then always M < P(M) [the power set of M]. Every set is of lower cardinality than the set of its subsets".
Zermelo proves this by considering a function φ: M → P(M). By Axiom III this defines the following set M' :
But no element m' of M could correspond to M' , i.e. such that φ(m' ) = M' . Otherwise we can construct a contradiction:
so by contradiction m' does not exist. Note the close resemblance of this proof to the way Zermelo disposes of Russell's paradox.
Ernst Zermelo
Ernst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...
, is the ancestor of modern set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted. This article sets out the original axioms, with the original text (translated into English) and original numbering.
The axioms of Zermelo set theory
- AXIOM I. Axiom of extensionalityAxiom of extensionalityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
(Axiom der Bestimmtheit) "If every element of a set M is also an element of N and vice versa ... then M
N. Briefly, every set is determined by its elements". - AXIOM II. Axiom of elementary sets (Axiom der Elementarmengen) "There exists a set, the null set, ∅, that contains no element at all. If a is any object of the domain, there exists a set {a} containing a and only a as element. If a and b are any two objects of the domain, there always exists a set {a, b} containing as elements a and b but no object x distinct from them both." See Axiom of pairsAxiom of pairingIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
. - AXIOM III. Axiom of separation (Axiom der Aussonderung) "Whenever the propositional functionPropositional functionA propositional function in logic, is a statement expressed in a way that would assume the value of true or false, except that within the statement is a variable that is not defined or specified, which leaves the statement undetermined...
–(x) is definite for all elements of a set M, M possesses a subset M' containing as elements precisely those elements x of M for which –(x) is true". - AXIOM IV. Axiom of the power setAxiom of power setIn mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
(Axiom der Potenzmenge) "To every set T there corresponds a set T' , the power set of T, that contains as elements precisely all subsets of T". - AXIOM V. Axiom of the unionAxiom of unionIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
(Axiom der Vereinigung) "To every set T there corresponds a set ∪T, the union of T, that contains as elements precisely all elements of the elements of T". - AXIOM VI. Axiom of choice (Axiom der Auswahl): "If T is a set whose elements all are sets that are different from ∅ and mutually disjoint, its union ∪T includes at least one subset S1 having one and only one element in common with each element of T".
- AXIOM VII. Axiom of infinityAxiom of infinityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
(Axiom des Unendlichen) "There exists in the domain at least one set Z that contains the null set as an element and is so constituted that to each of its elements a there corresponds a further element of the form {a}, in other words, that with each of its elements a it also contains the corresponding set {a} as element".
Connection with standard set theory
The accepted standard for set theory is Zermelo-Fraenkel set theory. The links show where the axioms of Zermelo's theory correspond. There is no exact match for "elementary sets". (It was later shown that the singleton set could be derived from what is now called "Axiom of pairs". If a exists, a and a exist, thus {a,a} exists. By extensionality {a,a} = {a}.) The empty set axiom is already assumed by axiom of infinity, and is now included as part of it.The axioms do not include the Axiom of regularity
Axiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
and Axiom of replacement. These were added as the result of work by Thoralf Skolem
Thoralf Skolem
Thoralf Albert Skolem was a Norwegian mathematician known mainly for his work on mathematical logic and set theory.-Life:...
in 1922, based on earlier work by Abraham Fraenkel in the same year.
In the modern ZFC system, the "propositional function" referred to in the axiom of separation is interpreted as "any property definable by a first order formula with parameters", so the separation axiom is replaced by an axiom scheme. The notion of "first order formula" was not known in 1904 when Zermelo published his axiom system, and he later rejected this interpretation as being too restrictive. Zermelo set theory is usually taken to be a first-order theory with the separation axiom replaced by an axiom scheme with an axiom for each first-order formula. It can also be considered as a theory in second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
, where now the separation axiom is just a single axiom. The second-order interpretation of Zermelo set theory is probably closer to Zermelo's own conception of it, and is stronger than the first-order interpretation.
In the usual cumulative hierarchy
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
Vα of ZFC set theory (for ordinals α), any one of the sets
Vα for α a limit ordinal larger than the first infinite ordinal ω (such as Vω·2) forms a model of Zermelo set theory. So the consistency of Zermelo set theory is a theorem of ZFC set theory. Zermelo's axioms do not imply the existence of ℵω or larger infinite cardinals, as the model Vω·2 does not contain such cardinals. (Cardinals have to be defined differently in Zermelo set theory, as the usual definition of cardinals and ordinals does not work very well: with the usual definition it is not even possible to prove the existence of the ordinal ω2.)
The axiom of infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
is usually now modified to assert the existence of the first infinite
von Neumann ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
; the original Zermeloaxioms cannot prove the existence of this set, nor can the modified Zermelo axioms prove Zermelo's
axiom of infinity. Zermelo's axioms (original or modified) cannot prove the existence of
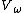as a set nor of any rank of the cumulative hierarchy of sets with infinite index.Zermelo set theory is similar in strength to topos theory with a natural number object
Natural number object
In category theory, a natural number object is an object endowed with a recursive structure similar to natural numbers. More precisely, in a category E with a terminal object 1 , an NNO N is given by:...
, or to the system in Principia mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
. It is strong enough to carry out almost all ordinary mathematics not directly connected with set theory or logic.
The aim of Zermelo's paper
The introduction states that the very existence of the discipline of set theory "seems to be threatened by certain contradictions or "antinomies", that can be derived from its principles – principles necessarily governing our thinking, it seems – and to which no entirely satisfactory solution has yet been found". Zermelo is of course referring to the "Russell antinomyRussell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
".
He says he wants to show how the original theory of Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
and Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
can be reduced to a few definitions and seven principles or axioms. He says he has not been able to prove that the axioms are consistent.
A non-constructivist argument for their consistency goes as follows. Define Vα for α one of the ordinals 0, 1, 2, ...,ω, ω+1, ω+2,..., ω·2 as follows:
- V0 is the empty set.
- For α a successor of the form β+1, Vα is defined to be the collection of all subsets of Vβ.
- For α a limit (e.g. ω, ω·2) then Vα is defined to be the union of Vβ for β<α.
Then the axioms of Zermelo set theory are consistent because they are true in the model Vω·2. While a non-constructivist might regard this as a valid argument, a constructivist would probably not: while there are no problems with the construction of the sets up to Vω, the construction of Vω+1 is less clear because one cannot constructively define every subset of Vω. This argument can be turned into a valid proof in Zermelo-Frenkel set theory, but this does not really help because the consistency of Zermelo-Frenkel set theory is less clear than the consistency of Zermelo set theory.
The axiom of separation
Zermelo comments that Axiom III of his system is the one responsible for eliminating the antinomies. It differs from the original definition by Cantor, as follows.Sets cannot be independently defined by any arbitrary logically definable notion. They must be constructed in some way from previously constructed sets. For example they can be constructed by taking powersets, or they can be separated as subsets of sets already "given". This, he says, eliminates contradictory ideas like "the set of all sets" or "the set of all ordinal numbers".
He disposes of the Russell paradox by means of this Theorem: "Every set
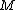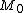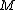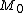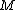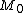possesses at least one subset that is not an element of ". Let be the subset of for which, by AXIOM III, is separated out by the notion "". Then cannot be in 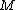. For- If
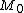is in 
, then 
contains an element x for which x is in x (i.e.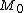 
itself), which would contradict the definition of 
. - If
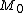is not in 
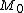, and assuming 
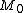is an element of M, then 
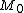is an element of M that satisfies the definition "
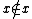", and so is in 
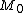which is a contradiction.
Therefore the assumption that
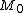is in 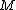is wrong, proving the theorem. Hence not all objects of the universal domain B can be elements of one and the same set. "This disposes of the Russell antinomyAntinomy
Antinomy literally means the mutual incompatibility, real or apparent, of two laws. It is a term used in logic and epistemology....
as far as we are concerned".
This left the problem of "the domain B" which seems to refer to something. This led to the idea of a proper class.
Cantor's theorem
Zermelo's paper is notable for what may be the first mention of Cantor's theoremCantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
explicitly and by name. This appeals strictly to set theoretical notions, and is thus not exactly the same as Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
.
Cantor's theorem: "If M is an arbitrary set, then always M < P(M) [the power set of M]. Every set is of lower cardinality than the set of its subsets".
Zermelo proves this by considering a function φ: M → P(M). By Axiom III this defines the following set M' :
- M' = {m: m ∉ φ(m)}.
But no element m' of M could correspond to M' , i.e. such that φ(m' ) = M' . Otherwise we can construct a contradiction:
- 1) If m' is in M' then by definition m' ∉ φ(m' ) = M' , which is the first part of the contradiction
- 2) If m' is in not in M' but in M then by definition m' ∉ M' = φ(m' ) which by definition implies that m' is in M' , which is the second part of the contradiction.
so by contradiction m' does not exist. Note the close resemblance of this proof to the way Zermelo disposes of Russell's paradox.