
Matthew Foreman
Encyclopedia
Matthew Dean Foreman is a set theorist
at University of California, Irvine
. He has made contributions in widely varying areas of set theory, including descriptive set theory
, forcing
, and infinitary combinatorics.
Foreman earned his Ph.D.
in 1980 at University of California, Berkeley
under the direction of Robert M. Solovay
, with a dissertation on Large Cardinals and Model Theoretic Transfer Properties.
Among Foreman's theorems are the following:
(All the consistency proofs start from the assumption that certain large cardinals are consistent with ZFC; e.g., the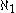 -dense ideal on
-dense ideal on 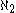 uses a huge cardinal.)
uses a huge cardinal.)
With Akihiro Kanamori
he is the editor of the monumental Handbook of Set Theory (2010).
He is also an avid sailor.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
at University of California, Irvine
University of California, Irvine
The University of California, Irvine , founded in 1965, is one of the ten campuses of the University of California, located in Irvine, California, USA...
. He has made contributions in widely varying areas of set theory, including descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
, forcing
Forcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
, and infinitary combinatorics.
Foreman earned his Ph.D.
Ph.D.
A Ph.D. is a Doctor of Philosophy, an academic degree.Ph.D. may also refer to:* Ph.D. , a 1980s British group*Piled Higher and Deeper, a web comic strip*PhD: Phantasy Degree, a Korean comic series* PhD Docbook renderer, an XML renderer...
in 1980 at University of California, Berkeley
University of California, Berkeley
The University of California, Berkeley , is a teaching and research university established in 1868 and located in Berkeley, California, USA...
under the direction of Robert M. Solovay
Robert M. Solovay
Robert Martin Solovay is an American mathematician specializing in set theory.Solovay earned his Ph.D. from the University of Chicago in 1964 under the direction of Saunders Mac Lane, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem...
, with a dissertation on Large Cardinals and Model Theoretic Transfer Properties.
Among Foreman's theorems are the following:
- It is consistent that for every uncountable regular cardinal κ there is a κ-complete, κ+-saturated ideal on κ.
- It is consistent that the Generalized Continuum Hypothesis fails everywhere (with W. Hugh WoodinW. Hugh WoodinWilliam Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...
). - A Banach-Tarski decompositionBanach–Tarski paradoxThe Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
is possible in which all pieces have the Baire property (with Randall DoughertyRandall DoughertyRandall Dougherty has made contributions in widely varying areas of mathematics, including set theory,logic, real analysis, discrete mathematics, computational geometry, information theory and coding theory....
). This problem of MarczewskiEdward MarczewskiEdward Marczewski was a Polish mathematician. His surname until 1940 was Szpilrajn.Marczewski was a member of the Warsaw School of Mathematics...
had been open for more than 60 years. - With Menachem MagidorMenachem MagidorMenachem Magidor is an Israeli mathematician who specializes in mathematical logic, in particular set theory. He served as President of the Hebrew University of Jerusalem.- Biography :Menachem Magidor was born in Petah Tikva on January 24, 1946....
and Saharon ShelahSaharon ShelahSaharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
he formulated and proved the consistency of Martin's maximumMartin's maximumIn set theory, Martin's maximum, introduced by , is a generalization of the proper forcing axiom, which is in turn a generalization of Martin's axiom....
, a provably maximal form of Martin's axiomMartin's axiomIn the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
. - It is consistent that there exists a
 -complete,
-complete, 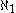 -dense ideal on
-dense ideal on 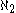 .
. - The collection of distal flows is not BorelBorel algebraIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
. (With his Ph. D. student, Ferenc Beleznay.)
(All the consistency proofs start from the assumption that certain large cardinals are consistent with ZFC; e.g., the
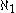 -dense ideal on
-dense ideal on 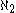 uses a huge cardinal.)
uses a huge cardinal.)With Akihiro Kanamori
Akihiro Kanamori
is a Japan-born American mathematician. He specializes in set theory and is the author of the successful monograph on large cardinals, The Higher Infinite. He wrote several essays on the history of mathematics, especially set theory.Kanamori graduated from California Institute of Technology and...
he is the editor of the monumental Handbook of Set Theory (2010).
He is also an avid sailor.

