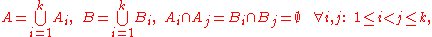Banach–Tarski paradox - AbsoluteAstronomy.com

The Banach–Tarski paradox is a theorem

Theorem

In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...

in set theoretic

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

which states the following: Given a solid ball

Ball (mathematics)

In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....

in 3-dimensional space, there exists

Existence theorem

In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...

a decomposition of the ball into a finite number of non-overlapping pieces (i.e., subsets), which can then be put back together in a different way to yield two identical copies of the original ball. The reassembly process involves only moving the pieces around and rotating them, without changing their shape. However, the pieces themselves are complicated: they are not usual solids but infinite scatterings of points. A stronger form of the theorem implies that given any two "reasonable" solid objects (such as a small ball and a huge ball) — solid in the sense of the continuum

Continuum hypothesis

In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...

— either one can be reassembled into the other. This is often stated colloquially as "a pea can be chopped up and reassembled into the Sun".

The reason the Banach–Tarski theorem is called a paradox

Paradox

Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...

is that it contradicts basic geometric intuition. "Doubling the ball" by dividing it into parts and moving them around by rotation

Rotation

A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

s and translation

Translation (geometry)

In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...

s, without any stretching, bending, or adding new points, seems to be impossible, since all these operations preserve the volume

Volume

Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....

, but the volume is doubled in the end.

Unlike most theorems in geometry, this result depends in a critical way on the axiom of choice in set theory. This axiom allows for the construction of nonmeasurable sets, collections of points that do not have a volume in the ordinary sense and require an uncountably infinite number of arbitrary choices to specify. Robert Solovay showed that the axiom of choice, or a weaker variant of it, is necessary for the construction of nonmeasurable sets by constructing a model of ZF set theory

Zermelo–Fraenkel set theory

In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...

(without choice) in which every geometric subset has a well-defined Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

. On the other hand, Solovay's construction relies on the assumption that an inaccessible cardinal

Inaccessible cardinal

In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...

exists (which itself cannot be proven from ZF set theory); Saharon Shelah

Saharon Shelah

Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...

later showed that this assumption is necessary.

The existence of nonmeasurable sets, such as those in the Banach–Tarski paradox, has been used as an argument against the axiom of choice. Nevertheless, most mathematicians are willing to tolerate the existence of nonmeasurable sets, given that the axiom of choice has many other mathematically useful consequences.

It was shown in 2005 that the pieces in the decomposition can be chosen in such a way that they can be moved continuously into place without running into one another.

Banach and Tarski publication

In a paper published in 1924, Stefan Banach

Stefan Banach

Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....

and Alfred Tarski

Alfred Tarski

Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...

gave a construction of such a "paradoxical decomposition", based on earlier work by Giuseppe Vitali

Giuseppe Vitali

Giuseppe Vitali was an Italian mathematician who worked in several branches of mathematical analysis.- Mathematical contributions :...

concerning the unit interval

Unit interval

In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...

and on the paradoxical decompositions of the sphere by Felix Hausdorff

Felix Hausdorff

Felix Hausdorff was a Jewish German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.-Life:Hausdorff studied at the University of Leipzig,...

, and discussed a number of related questions concerning decompositions of subsets of Euclidean spaces in various dimensions. They proved the following more general statement, the strong form of the Banach–Tarski paradox:

Given any two bounded

Bounded set

In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...

subsets A and B of a Euclidean space in at least three dimensions, both of which have a non-empty interior

Interior (topology)

In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....

, there are partitions of A and B into a finite number of disjoint subsets, A = A₁ ∪ ... ∪ A_k, B = B₁ ∪ ... ∪ B_k, such that for each i between 1 and k, the sets A_i and B_i are congruent

Congruence (geometry)

In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

Now let A be the original ball and B be the union of two translated copies of the original ball. Then the proposition means that you can divide the original ball A into a certain number of pieces and then rotate and translate these pieces in such a way that the result is the whole set B, which contains two copies of A.

The strong form of the Banach–Tarski paradox is false in dimensions one and two, but Banach and Tarski showed that an analogous statement remains true if countably many subsets are allowed. The difference between the dimensions 1 and 2 on the one hand, and three and higher, on the other hand, is due to the richer structure of the group G_n of the Euclidean motions in the higher dimensions, which is solvable

Solvable group

In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...

for n =1, 2 and contains a free group

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

with two generators for n ≥ 3. John von Neumann

John von Neumann

John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...

studied the properties of the group of equivalences that make a paradoxical decomposition possible, identifying the class of amenable group

Amenable group

In mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...

s, for which no paradoxical decompositions exist. He also found a form of the paradox in the plane which uses area-preserving affine transformation

Affine transformation

In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...

s in place of the usual congruences.

Formal treatment

The Banach–Tarski paradox states that a ball in the ordinary Euclidean space can be doubled using only the operations of partitioning into subsets, replacing a set with a congruent set, and reassembly. Its mathematical structure is greatly elucidated by emphasizing the role played by the group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

of Euclidean motions and introducing the notions of equidecomposable sets and paradoxical set
Paradoxical set
In set theory, a paradoxical set is a set that has a paradoxical decomposition. A paradoxical decomposition of a set is a partitioning of the set into exactly two subsets, along with an appropriate group of functions that operate on some universe , such that each partition can be mapped back onto...

. Suppose that G is a group acting

Group action

In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...

on a set X. In the most important special case, X is an n-dimensional Euclidean space, and G consists of all isometries

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

of X, i.e. the transformations of X into itself that preserve the distances. Two geometric figures that can be transformed into each other are called congruent

Congruence (geometry)

In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

, and this terminology will be extended to the general G-action. Two subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

s A and B of X are called G-equidecomposable, or equidecomposable with respect to G, if A and B can be partitioned into the same finite number of respectively G-congruent pieces. It is easy to see that this defines an equivalence relation

Equivalence relation

In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...

among all subsets of X. Formally, if

and there are elements g₁,...,g_k of G such that for each i between 1 and k, g_i (A_i ) = B_i , then we will say that A and B are G-equidecomposable using k pieces. If a set E has two disjoint subsets A and B such that A and E, as well as B and E, are G-equidecomposable then E is called paradoxical.

Using this terminology, the Banach–Tarski paradox can be reformulated as follows:

A three-dimensional Euclidean ball is equidecomposable with two copies of itself.

In fact, there is a sharp result in this case, due to Robinson: doubling the ball can be accomplished with five pieces, and fewer than five pieces will not suffice.

The strong version of the paradox claims:

Any two bounded subsets of 3-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

with non-empty

Empty set

In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...

interiors are equidecomposable.

While apparently more general, this statement is derived in a simple way from the doubling of a ball by using a generalization of Bernstein–Schroeder theorem due to Banach that implies that if A is equidecomposable with a subset of B and B is equidecomposable with a subset of A, then A and B are equidecomposable.

The Banach–Tarski paradox can be put in context by pointing out that for two sets in the strong form of the paradox, there is always a bijective function that can map the points in one shape into the other in a one-to-one fashion. In the language of Georg Cantor

Georg Cantor

Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...

's set theory

Set theory

, these two sets have equal cardinality. Thus, if one enlarges the group to allow arbitrary bijections of X then all sets with non-empty interior become congruent. Likewise, we can make one ball into a larger or smaller ball by stretching, in other words, by applying similarity

Similarity

-Specific definitions:Different fields provide differing definitions of similarity:-In computer science:* string metric, aka string similarity* semantic similarity in computational linguistics-In other fields:...

transformations. Hence if the group G is large enough, we may find G-equidecomposable sets whose "size" varies. Moreover, since a countable set

Countable set

In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...

can be made into two copies of itself, one might expect that somehow, using countably many pieces could do the trick. On the other hand, in the Banach–Tarski paradox the number of pieces is finite and the allowed equivalences are Euclidean congruences, which preserve the volumes. Yet, somehow, they end up doubling the volume of the ball! While this is certainly surprising, some of the pieces used in the paradoxical decomposition are non-measurable set

Non-measurable set

In mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....

s, so the notion of volume (more precisely, Lebesgue measure

Lebesgue measure

) is not defined for them, and the partitioning cannot be accomplished in a practical way. In fact, the Banach–Tarski paradox demonstrates that it is impossible to find a finitely-additive measure (or a Banach measure

Banach measure

In mathematics, Banach measure in measure theory may mean a real-valued function on the algebra of all sets , by means of which a rigid, finitely additive area can be defined for every set, even when a set does not have a true geometric area. That is, this is a theoretical definition getting round...

) defined on all subsets of a Euclidean space of three (and greater) dimensions that is invariant with respect to Euclidean motions and takes the value one on a unit cube. In his later work, Tarski showed that, conversely, non-existence of paradoxical decompositions of this type implies the existence of a finitely-additive invariant measure.

The heart of the proof of the "doubling the ball" form of the paradox presented below is the remarkable fact that by a Euclidean isometry (and renaming of elements), one can divide a certain set (essentially, the surface of a unit sphere) into four parts, then rotate one of them to become itself plus two of the other parts. This follows rather easily from a F₂-paradoxical decomposition of F₂, the free group

Free group

with two generators. Banach and Tarski's proof relied on an analogous fact discovered by Hausdorff some years earlier: the surface of a unit sphere in space is a disjoint union of three sets B, C, D and a countable set

Countable set

E such that, on the one hand, B, C, D are pairwise congruent, and, on the other hand, B is congruent with the union of C and D. This is often called the Hausdorff paradox
Hausdorff paradox
In mathematics, the Hausdorff paradox, named after Felix Hausdorff, states that if you remove a certain countable subset of the sphere S2, the remainder can be divided into three disjoint subsets A, B and C such that A, B, C and B ∪ C are all congruent...

.

Connection with earlier work and the role of the axiom of choice

Banach and Tarski explicitly acknowledge Giuseppe Vitali

Giuseppe Vitali

Giuseppe Vitali was an Italian mathematician who worked in several branches of mathematical analysis.- Mathematical contributions :...

's 1905 construction of the set bearing his name

Vitali set

In mathematics, a Vitali set is an elementary example of a set of real numbers that is not Lebesgue measurable, found by . The Vitali theorem is the existence theorem that there are such sets. There are uncountably many Vitali sets, and their existence is proven on the assumption of the axiom of...

, Hausdorff's paradox (1914), and an earlier (1923) paper of Banach as the precursors to their work. Vitali's and Hausdorff's constructions depend on Zermelo's axiom of choice ("AC"), which is also crucial to the Banach–Tarski paper, both for proving their paradox and for the proof of another result:

Two Euclidean polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

s, one of which strictly contains the other, are not equidecomposable.

They remark:

Le rôle que joue cet axiome dans nos raisonnements nous semble mériter l'attention

(The role this axiom plays in our reasoning seems to us to deserve attention)

and point out that while the second result fully agrees with our geometric intuition, its proof uses AC in even more substantial way than the proof of the paradox. Thus Banach and Tarski imply that AC should not be rejected simply because it produces a paradoxical decomposition. Indeed, such an argument would also reject some geometrically intuitive statements!

However, in 1949 A.P. Morse showed that the statement about Euclidean polygons can be proved in ZF set theory

Zermelo–Fraenkel set theory

and thus does not require the axiom of choice. In 1964, Paul Cohen

Paul Cohen (mathematician)

Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...

proved the equiconsistency of the axiom of choice with the rest of set theory, which implies that ZFC (ZF set theory with the axiom of choice) is consistent if and only if ZF theory without choice is consistent. Using Cohen's technique of forcing

Forcing (mathematics)

In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...

, Robert M. Solovay

Robert M. Solovay

Robert Martin Solovay is an American mathematician specializing in set theory.Solovay earned his Ph.D. from the University of Chicago in 1964 under the direction of Saunders Mac Lane, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem...

later established, under the assumption that the existence of an inaccessible cardinal

Inaccessible cardinal

is consistent, that in the absence of choice it is consistent to be able to assign a Lebesgue measure to any subset in Rⁿ, contradicting the Banach–Tarski paradox (BT). Solovay's results extend to ZF supplemented by a weak form of AC called the axiom of dependent choice

Axiom of dependent choice

In mathematics, the axiom of dependent choices, denoted DC, is a weak form of the axiom of choice which is still sufficient to develop most of real analysis...

, DC. It follows that

Banach–Tarski paradox is not a theorem of ZF, nor of ZF+DC (Wagon, Corollary 13.3).

Most mathematicians currently accept AC. As Stan Wagon points out at the end of his monograph, the Banach–Tarski paradox is more significant for its role in pure mathematics than it is to foundational questions. As far as the axiom of choice is concerned, BT plays the same role as the existence of non-measurable sets. But the Banach–Tarski paradox is more significant for the rest of mathematics because it motivated a fruitful new direction for research, amenability of groups, which has nothing to do with the foundational questions.

In 1991, using then-recent results by Matthew Foreman

Matthew Foreman

Matthew Dean Foreman is a set theorist at University of California, Irvine. He has made contributions in widely varying areas of set theory, including descriptive set theory, forcing, and infinitary combinatorics....

and Friedrich Wehrung, Janusz Pawlikowski proved that the Banach–Tarski paradox follows from ZF plus the Hahn–Banach theorem

Hahn–Banach theorem

In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...

. The Hahn–Banach theorem doesn't rely on the full axiom of choice but can be proved using a weaker version of AC called the ultrafilter lemma. So Pawlikowski proved that the set theory needed to prove the Banach–Tarski paradox, while stronger than ZF, is weaker than full ZFC.

A sketch of the proof

Here we sketch a proof which is similar but not identical to that given by Banach and Tarski. Essentially, the paradoxical decomposition of the ball is achieved in four steps:

Find a paradoxical decomposition of the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

in two generators
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...

.
Find a group of rotations in 3-d space isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...

to the free group in two generators.
Use the paradoxical decomposition of that group and the axiom of choice to produce a paradoxical decomposition of the hollow unit sphere.
Extend this decomposition of the sphere to a decomposition of the solid unit ball.

We now discuss each of these steps in more detail.

Step 1

The free group with two generators

Generating set of a group

In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...

a and b consists of all finite strings that can be formed from the four symbols a, a⁻¹, b and b⁻¹ such that no a appears directly next to an a⁻¹ and no b appears directly next to a b⁻¹. Two such strings can be concatenated and converted into a string of this type by repeatedly replacing the "forbidden" substrings with the empty string. For instance: abab⁻¹a⁻¹ concatenated with abab⁻¹a yields abab⁻¹a⁻¹abab⁻¹a, which contains the substring a⁻¹a, and so gets reduced to abaab⁻¹a. One can check that the set of those strings with this operation forms a group with identity element

Identity element

In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...

the empty string e. We will call this group F₂.
The group

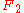can be "paradoxically decomposed" as follows: let S(a) be the set of all strings that start with a and define S(a⁻¹), S(b) and S(b⁻¹) similarly. Clearly,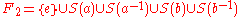

but also

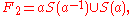
and

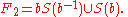
The notation aS(a⁻¹) means take all the strings in S(a⁻¹) and concatenate them on the left with a.

Make sure that you understand this last line, because it is at the core of the proof. For example, there may be a string

in the set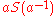

which, because of the rule that

must not appear next to

, reduces to the string

. In this way,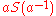

contains all the strings that start with

. Similarly, it contains all the strings that start with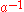

(for example the string

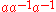which reduces to

).

We have cut our group F₂ into four pieces (plus the singleton {e}), then "shifted" two of them by multiplying with a or b, then "reassembled" two pieces to make one copy of

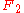and the other two to make another copy of

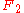. That is exactly what we want to do to the ball.

Step 2

In order to find a group of rotations of 3D space that behaves just like (or "isomorphic to") the group

, we take two orthogonal axes, e.g. the x and z axes, and let A be a rotation of arccos(1/3) about the first, x axis, and B be a rotation of arccos(1/3) about the second, z axis (there are many other suitable pairs of irrational multiples of π, that could be used here instead of arccos(1/3) and arccos(1/3), as well). It is somewhat messy but not too difficult to show that these two rotations behave just like the elements a and b in our group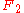

. We shall skip it, leaving the exercise to the reader. The new group of rotations generated by A and B will be called H. We now also have a paradoxical decomposition of H. (This step cannot be performed in two dimensions since it involves rotations in three dimensions. If we take two rotations about the same axis, the resulting group is commutative and doesn't have the property required in step 1.)

Step 3

The unit sphere

Unit sphere

In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...

S² is partitioned into orbits by the action

Group action

of our group H: two points belong to the same orbit if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

there's a rotation in H which moves the first point into the second. (Note that the orbit of a point is a dense set

Dense set

In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...

in S².) We can use the axiom of choice to pick exactly one point from every orbit; collect these points into a set M. Now (almost) every point in S² can be reached in exactly one way by applying the proper rotation from H to the proper element from M, and because of this, the paradoxical decomposition of H then yields a paradoxical decomposition of S². The (majority of the) sphere can be divided into four sets (each one dense on the sphere), and when two of these are rotated, we end up with double what we had before.

Step 4

Finally, connect every point on S² with a ray to the origin; the paradoxical decomposition of S² then yields a paradoxical decomposition of the solid unit ball minus the point at the ball's centre (this center point needs a bit more care, see below).

N.B.
Nota Bene
Nota bene is an Italian and Latin phrase meaning "note well". The phrase first appeared in writing circa 1721.Often abbreviated as "N. B.", nota bene comes from the Latin roots notāre and bene . It is in the singular imperative mood, instructing one individual to note well the matter at hand...

This sketch glosses over some details. One has to be careful about the set of points on the sphere which happen to lie on the axis of some rotation in H. However, there are only countably many such points, and like the point at the centre of the ball, it is possible to patch the proof to account for them all (see below).

Some details, fleshed out

In Step 3, we partitioned the sphere into orbits of our group H. To streamline the proof, we omitted the discussion of points that are fixed by some rotation; since the paradoxical decomposition of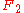

relies on shifting certain subsets, the fact that some points are fixed might cause some trouble. Since any rotation of S² (other than the null rotation) has exactly two fixed points

Fixed point (mathematics)

In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...

, and since H, which is isomorphic to

, is countable, there are countably many points of S² that are fixed by some rotation in H, denote this set of fixed points D. Step 3 proves that S² − D admits a paradoxical decomposition.

What remains to be shown is the Claim: S² − D is equidecomposable with S².

Proof. Let λ be some line through the origin that does not intersect any point in D—this is possible since D is countable. Let J be the set of angles, α, such that for some natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

n, and some P in D, r(nα)P is also in D, where r(nα) is a rotation about λ of nα. Then J is countable so there exists an angle θ not in J. Let ρ be the rotation about λ by θ, then ρ acts on S² with no fixed points

Fixed point (mathematics)

In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...

in D, i.e., ρⁿ(D) is disjoint from D, and for natural m<n, ρⁿ(D) is disjoint from ρ^m(D). Let E be the disjoint union

Disjoint union

In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...

of ρⁿ(D) over n = 0,1,2,.... Then S² = E ∪ (S² − E) ~ ρ(E) ∪ (S² − E) = (E − D) ∪ (S² − E) = S² − D, where ~ denotes "is equidecomposable to".

For step 4, it has already been shown that the ball minus a point admits a paradoxical decomposition; it remains to be shown that the ball minus a point is equidecomposable with the ball. Consider a circle within the ball, containing the point at the centre of the ball. Using an argument like that used to prove the Claim, one can see that the full circle is equidecomposable with the circle minus the point at the ball's centre. (Basically, a countable set of points on the circle can be rotated to give itself plus one more point.)
Note that this involves the rotation about a point other than the origin, so the Banach–Tarski paradox involves isometries of Euclidean 3-space rather than just SO(3).

We are using the fact that if A ~ B and B ~ C, then A ~ C. The decomposition of A into C can be done using number of pieces equal to the product of the numbers needed for taking A into B and for taking B into C.

The proof sketched above requires 2×4×2 + 8 = 24 pieces, a factor of 2 to remove fixed points, a factor 4 from step 1, a factor 2 to recreate fixed points, and 8 for the center point of the second ball. But in step 1 when moving {e} and all strings of the form aⁿ into S(a⁻¹), do this to all orbits except one. Move {e} of this last orbit to the center point of the second ball. This brings the total down to 16 + 1 pieces. With more algebra one can also decompose fixed orbits into 4 sets as in step 1. This gives 5 pieces and is the best possible.

Obtaining infinitely many balls from one

Using the Banach–Tarski paradox, it is possible to obtain k copies of a ball in the Euclidean n-space from one, for any integers n ≥ 3 and k ≥ 1, i.e. a ball can be cut into k pieces so that each of them is equidecomposable to a ball of the same size as the original. Using the fact that the free group

Free group

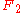of rank 2 admits a free subgroup of countably infinite rank, a similar proof yields that the unit sphere Sⁿ⁻¹ can be partitioned into countably infinitely many pieces, each of which is equidecomposable (with two pieces) to the Sⁿ⁻¹ using rotations. By using analytic properties of the rotation group SO(n), which is a connected

Connected space

In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...

analytic Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

, one can further prove that the sphere Sⁿ⁻¹ can be partitioned into as many pieces as there are real numbers (that is,

pieces), so that each piece is equidecomposable with two pieces to Sⁿ⁻¹ using rotations. These results then extend to the unit ball deprived of the origin. In 2010 an article of Vitaly Churkin was published that gives a new proof of the continuous version of the Banach–Tarski paradox.

The von Neumann paradox in the Euclidean plane

In the Euclidean plane, two figures that are equidecomposable with respect to the group of Euclidean motions are necessarily of the same area, therefore, a paradoxical decomposition of a square or disk of Banach–Tarski type that uses only Euclidean congruences is impossible. A conceptual explanation of the distinction between the planar and higher-dimensional cases was given by John von Neumann

John von Neumann

: unlike the group SO(3) of rotations in three dimensions, the group E(2) of Euclidean motions of the plane is solvable

Solvable group

In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...

, which implies the existence of a finitely-additive measure on E(2) and R² which is invariant under translations and rotations, and rules out paradoxical decompositions of non-negligible sets. Von Neumann then posed the following question: can such a paradoxical decomposition be constructed if one allowed a larger group of equivalences?

It is clear that if one permits similarities

Similarity (geometry)

Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...

, any two squares in the plane become equivalent even without further subdivision. This motivates restricting one's attention to the group SA₂ of area-preserving affine transformations

Special affine group

In the mathematical study of transformation groups, the special affine group is the group of affine transformations of a fixed affine space which preserve volume...

. Since the area is preserved, any paradoxical decomposition of a square with respect to this group would be counterintuitive for the same reasons as the Banach–Tarski decomposition of a ball. In fact, the group SA₂ contains as a subgroup the special linear group SL(2,R), which in its turn contains the free group

Free group

F₂ with two generators as a subgroup. This makes it plausible that the proof of Banach–Tarski paradox can be imitated in the plane. The main difficulty here lies in the fact that the unit square is not invariant under the action of the linear group SL(2,R), hence one cannot simply transfer a paradoxical decomposition from the group to the square, as in the third step of the above proof of the Banach–Tarski paradox. Moreover, the fixed points of the group present difficulties (for example, the origin is fixed under all linear transformations). This is why von Neumann used the larger group SA₂ including the translations, and he constructed a paradoxical decomposition of the unit square with respect to the enlarged group (in 1929). Applying the Banach–Tarski method, the paradox for the square can be strengthened as follows:

Any two bounded subsets of the Euclidean plane with non-empty interiors are equidecomposable with respect to the area-preserving affine maps.

As von Neumann notes,

"Infolgedessen gibt es bereits in der Ebene kein nichtnegatives additives Maß (wo das Einheitsquadrat das Maß 1 hat), dass [sic] gegenüber allen Abbildungen von A₂ invariant wäre."

"In accordance with this, already in the plane there is no nonnegative additive measure (for which the unit square has a measure of 1), which is invariant with respect to all transformations belonging to A₂ [the group of area-preserving affine transformations]."

To explain this a bit more, the question of whether a finitely additive measure exists, that is preserved under certain transformations, depends on what transformations are allowed. The Banach measure

Banach measure

of sets in the plane, which is preserved by translations and rotations, is not preserved by non-isometric transformations even when they do preserve the area of polygons. The points of the plane (other than the origin) can be divided into two dense set

Dense set

In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...

s which we may call A and B. If the A points of a given polygon are transformed by a certain area-preserving transformation and the B points by another, both sets can become subsets of the A points in two new polygons. The new polygons have the same area as the old polygon, but the two transformed sets cannot have the same measure as before (since they contain only part of the A points), and therefore there is no measure that "works".

The class of groups isolated by von Neumann in the course of study of Banach–Tarski phenomenon turned out to be very important for many areas of mathematics: these are amenable group

Amenable group

In mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...

s, or groups with an invariant mean, and include all finite and all solvable groups. Generally speaking, paradoxical decompositions arise when the group used for equivalences in the definition of equidecomposability is not amenable.

Recent progress

Von Neumann's paper left open the possibility of a paradoxical decomposition of the interior of the unit square with respect to the linear group SL(2,R) (Wagon, Question 7.4). In 2000, Miklós Laczkovich
Miklós Laczkovich
Miklós Laczkovich is a Hungarian mathematician mainly noted for his work on real analysis and geometric measure theory. His most famous result is the solution of Tarski's circle-squaring problem in 1989.- Career :...

proved that such a decomposition exists. More precisely, let A be the family of all bounded subsets of the plane with non-empty interior and at a positive distance from the origin, and B the family of all planar sets with the property that a union of finitely many translates under some elements of SL(2,R) contains a punctured neighbourhood of the origin. Then all sets in the family A are SL(2,R)-equidecomposable, and likewise for the sets in B. It follows that both families consist of paradoxical sets.

Topoi do not assume the axiom of choices, so categorical proofs done on topoi sometimes re-create desired results without the undesired assumption.

It had been known for a long time that the full plane was paradoxical with respect to SA₂, and that the minimal number of pieces would equal four provided that there exists a locally commutative free subgroup of SA₂. In 2003 Kenzi Satô constructed such a subgroup, confirming that four pieces suffice.

External links

The Banach-Tarski Paradox by Stan Wagon (Macalester College
Macalester College
Macalester College is a private, coeducational liberal arts college located in Saint Paul, Minnesota. It was founded in 1874 as a Presbyterian-affiliated but nonsectarian college. Its first class entered September 15, 1885. The college is located on a campus in a historic residential neighborhood...

), the Wolfram Demonstrations Project
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...

.
Irregular Webcomic! #2339 by David Morgan-Mar provides a non-technical explanation of the paradox. It includes a step-by-step demonstration of how to create two spheres from one.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Banach and Tarski publication

Formal treatment

Connection with earlier work and the role of the axiom of choice

A sketch of the proof

Step 1

Step 2

Step 3

Step 4

Some details, fleshed out

Obtaining infinitely many balls from one

The von Neumann paradox in the Euclidean plane

Recent progress

See also

External links