
Huge cardinal
Encyclopedia
In mathematics
, a cardinal number
κ is called huge if there exists an elementary embedding j : V → M from V into a transitive inner model
M with critical point
κ and
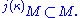
Here, αM is the class of all sequence
s of length α whose elements are in M.
Huge cardinals were introduced by .
with itself n times, for a finite ordinal n. Also, <αM is the class of all sequences of length less than α whose elements are in M. Notice that for the "super" versions, γ should be less than j(κ), not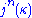 .
.
κ is almost n-huge if and only if there is j : V → M with critical point κ and

κ is super almost n-huge if and only if for every ordinal γ there is j : V → M with critical point κ, γ<j(κ), and
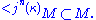
κ is n-huge if and only if there is j : V → M with critical point κ and
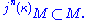
κ is super n-huge if and only if for every ordinal γ there is j : V → M with critical point κ, γ<j(κ), and
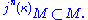
Notice that 0-huge is the same as measurable cardinal
; and 1-huge is the same as huge. A cardinal satisfying one of the rank into rank axioms is n-huge for all finite n.
The existence of an almost huge cardinal implies that Vopenka's principle
is consistent; more precisely any almost huge cardinal is also a Vopenka cardinal.
The consistency of a huge cardinal implies the consistency of a supercompact cardinal, nevertheless, the least huge cardinal is smaller than the least supercompact cardinal (assuming both exist).
shows that ω-huge cardinals are inconsistent in ZFC, though it is still open whether they are consistent in ZF.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
κ is called huge if there exists an elementary embedding j : V → M from V into a transitive inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
M with critical point
Critical point (set theory)
In set theory, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal which is not mapped to itself....
κ and
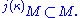
Here, αM is the class of all sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of length α whose elements are in M.
Huge cardinals were introduced by .
Variants
In what follows, jn refers to the n-th iterate of the elementary embedding j, that is, j composedFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
with itself n times, for a finite ordinal n. Also, <αM is the class of all sequences of length less than α whose elements are in M. Notice that for the "super" versions, γ should be less than j(κ), not
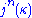 .
.κ is almost n-huge if and only if there is j : V → M with critical point κ and

κ is super almost n-huge if and only if for every ordinal γ there is j : V → M with critical point κ, γ<j(κ), and
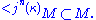
κ is n-huge if and only if there is j : V → M with critical point κ and
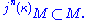
κ is super n-huge if and only if for every ordinal γ there is j : V → M with critical point κ, γ<j(κ), and
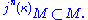
Notice that 0-huge is the same as measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
; and 1-huge is the same as huge. A cardinal satisfying one of the rank into rank axioms is n-huge for all finite n.
The existence of an almost huge cardinal implies that Vopenka's principle
Vopenka's principle
In mathematics, Vopěnka's principle, named after Petr Vopěnka, is a large cardinal axiom. A cardinal κ is called a Vopěnka cardinal if Vopěnka's principle holds in the rank Vκ .....
is consistent; more precisely any almost huge cardinal is also a Vopenka cardinal.
Consistency strength
The cardinals are arranged in order of increasing consistency strength as follows:- almost n-huge
- super almost n-huge
- n-huge
- super n-huge
- almost n+1-huge
The consistency of a huge cardinal implies the consistency of a supercompact cardinal, nevertheless, the least huge cardinal is smaller than the least supercompact cardinal (assuming both exist).
ω-huge cardinals
One can try defining an ω-huge cardinal κ as one such that an elementary embedding j : V → M from V into a transitive inner model M with critical point κ and λM⊆M, where λ is the supremum of jnκ for positive integers n. However Kunen's inconsistency theoremKunen's inconsistency theorem
In set theory, a branch of mathematics, Kunen's inconsistency theorem, proved by , shows that several plausible large cardinal axioms are inconsistent with the axiom of choice.Some consequences of Kunen's theorem are:...
shows that ω-huge cardinals are inconsistent in ZFC, though it is still open whether they are consistent in ZF.
See also
- List of large cardinal properties
- The Dehornoy orderDehornoy orderin mathematics, the Dehornoy order is a left-invariant total order on the braid group, found by .Dehornoy's original discovery of the order on the braid group used huge cardinals, but there are now several more elementary constructions of it.-Definition:...
on a braid group was motivated by properties of huge cardinals.

