Critical point (set theory)
Encyclopedia
In set theory
, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal
which is not mapped to itself.
Suppose that j : N → M is an elementary embedding where N and M are transitive classes and j is definable in N by a formula of set theory with parameters from N. Then j must take ordinals to ordinals and j must be strictly increasing. Also j(ω)=ω. If j(α)=α for all α<κ and j(κ)>κ, then κ is said to be the critical point of j.
If N is V
, then κ (the critical point of j) is always a measurable cardinal
, i.e. an uncountable cardinal number
κ such that there exists a <κ-complete, non-principal ultrafilter
over κ. Specifically, one may take the filter to be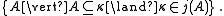
Generally, there will be many other <κ-complete, non-principal ultrafilters over κ. However, j might be different from the ultrapower(s) arising from such filter(s).
If N and M are the same and j is the identity function on N, then j is called "trivial". If transitive class N is an inner model
of ZFC and j has no critical point, i.e. every ordinal maps to itself, then j is trivial.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
which is not mapped to itself.
Suppose that j : N → M is an elementary embedding where N and M are transitive classes and j is definable in N by a formula of set theory with parameters from N. Then j must take ordinals to ordinals and j must be strictly increasing. Also j(ω)=ω. If j(α)=α for all α<κ and j(κ)>κ, then κ is said to be the critical point of j.
If N is V
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
, then κ (the critical point of j) is always a measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
, i.e. an uncountable cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
κ such that there exists a <κ-complete, non-principal ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
over κ. Specifically, one may take the filter to be
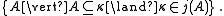Generally, there will be many other <κ-complete, non-principal ultrafilters over κ. However, j might be different from the ultrapower(s) arising from such filter(s).If N and M are the same and j is the identity function on N, then j is called "trivial". If transitive class N is an inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
of ZFC and j has no critical point, i.e. every ordinal maps to itself, then j is trivial.