
Menachem Magidor
Encyclopedia
Menachem Magidor is an Israel
i mathematician
who specializes in mathematical logic
, in particular set theory. He served as President of the Hebrew University of Jerusalem
.
on January 24, 1946.
He received his Ph.D.
in 1973 from the Hebrew University. His thesis, On Super Compact Cardinals, was written under the supervision of Azriel Levy
.
. He generalized the Prikry forcing in order to change the cofinality of a large cardinal to a predetermined regular cardinal. He proved that the least strongly compact cardinal
can be equal to the least measurable cardinal
or to the least supercompact cardinal (but not at the same time). He proved consistent that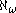 is strong limit, but
is strong limit, but 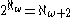 . He even strengthened the condition that
. He even strengthened the condition that 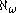 is strong limit to that GCH holds below
is strong limit to that GCH holds below 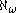 . This constituted a negative solution to the singular cardinals hypothesis. Both proofs used the consistency of very large cardinals. With Matthew Foreman
. This constituted a negative solution to the singular cardinals hypothesis. Both proofs used the consistency of very large cardinals. With Matthew Foreman
and Saharon Shelah
they formulated and proved the consistency of Martin's maximum
, a provably maximal form of Martin's axiom
. Magidor also gave a simple proof of the Jensen and the Dodd-Jensen covering lemma
s. He also proved that if 0#
does not exist then every primitive recursive closed set of ordinals is the union of countably many sets in L.
Israel
The State of Israel is a parliamentary republic located in the Middle East, along the eastern shore of the Mediterranean Sea...
i mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
who specializes in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, in particular set theory. He served as President of the Hebrew University of Jerusalem
Hebrew University of Jerusalem
The Hebrew University of Jerusalem ; ; abbreviated HUJI) is Israel's second-oldest university, after the Technion – Israel Institute of Technology. The Hebrew University has three campuses in Jerusalem and one in Rehovot. The world's largest Jewish studies library is located on its Edmond J...
.
Biography
Menachem Magidor was born in Petah TikvaPetah Tikva
Petah Tikva known as Em HaMoshavot , is a city in the Center District of Israel, east of Tel Aviv.According to the Central Bureau of Statistics, at the end of 2009, the city's population stood at 209,600. The population density is approximately...
on January 24, 1946.
He received his Ph.D.
Ph.D.
A Ph.D. is a Doctor of Philosophy, an academic degree.Ph.D. may also refer to:* Ph.D. , a 1980s British group*Piled Higher and Deeper, a web comic strip*PhD: Phantasy Degree, a Korean comic series* PhD Docbook renderer, an XML renderer...
in 1973 from the Hebrew University. His thesis, On Super Compact Cardinals, was written under the supervision of Azriel Levy
Azriel Levy
Azriel Levy is an Israeli mathematician, logician, and a professor emeritus at the Hebrew University of Jerusalem....
.
Mathematical theories
Magidor obtained several important consistency results on powers of singular cardinals substantially developing the method of forcingForcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
. He generalized the Prikry forcing in order to change the cofinality of a large cardinal to a predetermined regular cardinal. He proved that the least strongly compact cardinal
Strongly compact cardinal
In mathematical set theory, a strongly compact cardinal is a certain kind of large cardinal number; their existence can neither be proven nor disproven from the standard axioms of set theory....
can be equal to the least measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
or to the least supercompact cardinal (but not at the same time). He proved consistent that
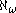 is strong limit, but
is strong limit, but 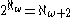 . He even strengthened the condition that
. He even strengthened the condition that 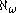 is strong limit to that GCH holds below
is strong limit to that GCH holds below 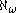 . This constituted a negative solution to the singular cardinals hypothesis. Both proofs used the consistency of very large cardinals. With Matthew Foreman
. This constituted a negative solution to the singular cardinals hypothesis. Both proofs used the consistency of very large cardinals. With Matthew ForemanMatthew Foreman
Matthew Dean Foreman is a set theorist at University of California, Irvine. He has made contributions in widely varying areas of set theory, including descriptive set theory, forcing, and infinitary combinatorics....
and Saharon Shelah
Saharon Shelah
Saharon Shelah is an Israeli mathematician. He is a professor of mathematics at the Hebrew University of Jerusalem and Rutgers University in New Jersey.-Biography:...
they formulated and proved the consistency of Martin's maximum
Martin's maximum
In set theory, Martin's maximum, introduced by , is a generalization of the proper forcing axiom, which is in turn a generalization of Martin's axiom....
, a provably maximal form of Martin's axiom
Martin's axiom
In the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
. Magidor also gave a simple proof of the Jensen and the Dodd-Jensen covering lemma
Covering lemma
In mathematics, under various anti-large cardinal assumptions, one can prove the existence of the canonical inner model, called the Core Model, that is, in a sense, maximal and approximates the structure of V...
s. He also proved that if 0#
Zero sharp
In the mathematical discipline of set theory, 0# is the set of true formulas about indiscernibles in the Gödel constructible universe. It is often encoded as a subset of the integers , or as a subset of the hereditarily finite sets, or as a real number...
does not exist then every primitive recursive closed set of ordinals is the union of countably many sets in L.

