
Stone–Cech compactification
Encyclopedia
In the mathematical discipline of general topology
, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact
Hausdorff space
βX. The Stone–Čech compactification βX of a topological space X is the largest compact Hausdorff space "generated" by X, in the sense that any map from X to a compact Hausdorff space factors through
βX (in a unique way). If X is a Tychonoff space
then the map from X to its image in βX is a homeomorphism, so X can be thought of as a (dense) subspace of βX. For general topological spaces X, the map from X to βX need not be injective.
A form of the axiom of choice is required to prove that every topological space has a Stone–Čech compactification. Even for quite simple spaces , an accessible concrete description of
, an accessible concrete description of 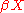 often remains elusive. In particular, proofs that
often remains elusive. In particular, proofs that  is nonempty do not give an explicit description of any particular point in
is nonempty do not give an explicit description of any particular point in 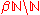 .
.
The Stone–Čech compactification was first considered by Tychonoff and later by and .
: any continuous map f : X → K, where K is a compact Hausdorff space, lifts uniquely to a continuous map βf : βX → K.
As is usual for universal properties, this universal property, together with the fact that βX is a compact Hausdorff space containing X, characterizes βX up to
homeomorphism
.
Some authors add the assumption that the starting space be Tychonoff (or even locally compact Hausdorff), for the following reasons:
The Stone–Čech construction can be performed for more general spaces X, but the map X → βX need not be a homeomorphism to the image of X (and sometimes is not even injective).
The extension property makes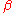 a functor
a functor
from Top (the category
of topological spaces) to CHaus (the category of compact Hausdorff spaces). If we let be the inclusion functor from CHaus into Top, maps from
be the inclusion functor from CHaus into Top, maps from 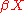 to
to  (for
(for  in CHaus) correspond bijectively to maps from
in CHaus) correspond bijectively to maps from  to
to  (by considering their restriction to
(by considering their restriction to  and using the universal property of
and using the universal property of 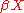 ). i.e.
). i.e. 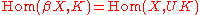 , which means that
, which means that 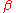 is left adjoint to
is left adjoint to  . This implies that CHaus is a reflective subcategory
. This implies that CHaus is a reflective subcategory
of Top with reflector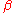 .
.

where the product is over all maps from X to compact Hausdorff spaces C. This works intuitively but fails for the technical reason that the collection of all such maps is a proper class rather than a set. There are several ways to modify this idea to make it work; for example, one can restrict the compact Hausdorff spaces C to have underlying set P(P(X)) (the power set of the power set of X), which is sufficiently large that it has cardinality at least equal to that of every compact Hausdorff set to which X can be mapped with dense image.
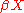 is to consider the map
is to consider the map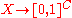
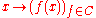
where is the set of all continuous function
is the set of all continuous function
s from into
into 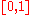 . This may be seen to be a continuous map onto its image, if
. This may be seen to be a continuous map onto its image, if 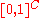 is given the product topology
is given the product topology
. By Tychonoff's theorem
we have that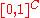 is compact since [0,1] is, so the closure of
is compact since [0,1] is, so the closure of  in
in  is a compactification of
is a compactification of  .
.
In order to verify that this is the Stone–Čech compactification, we just need to verify that it satisfies the appropriate universal property. We do this first for , where the desired extension of f : X → [0,1] is just the projection onto the
, where the desired extension of f : X → [0,1] is just the projection onto the  coordinate in
coordinate in  . In order to then get this for general compact Hausdorff
. In order to then get this for general compact Hausdorff  we use the above to note that
we use the above to note that  can be embedded in some cube, extend each of the coordinate functions and then take the product of these extensions.
can be embedded in some cube, extend each of the coordinate functions and then take the product of these extensions.
The special property of the unit interval needed for this construction to work is that it is a cogenerator of the category of compact Hausdorff spaces: this means that if f and g are any two distinct maps from compact Hausdorff spaces A to B, then there is a map h from B to [0,1] such that hf and hg are distinct. Any other cogenerator (or cogenerating set) can be used in this construction.
 is discrete, one can construct
is discrete, one can construct 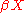 as the set of all ultrafilter
as the set of all ultrafilter
s on , with a topology known as Stone topology. The elements of
, with a topology known as Stone topology. The elements of  correspond to the principal ultrafilter
correspond to the principal ultrafilter
s.
Again we verify the universal property: For f : X → K with compact Hausdorff and
compact Hausdorff and  an ultrafilter on
an ultrafilter on  we have an ultrafilter
we have an ultrafilter 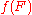 on
on  . This has a unique limit because
. This has a unique limit because  is compact, say
is compact, say  , and we define
, and we define 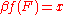 . This may be verified to be a continuous extension of
. This may be verified to be a continuous extension of  .
.
Equivalently, one can take the Stone space of the complete Boolean algebra
of all subsets of X as the
Stone–Čech compactification. This is really the same construction, as the Stone space of this Boolean algebra is the set of ultrafilters (or equivalently prime ideals, or homomorphisms to the 2 element Boolean algebra) of the Boolean algebra, which is the same as the set of ultrafilters on X.
The construction can be generalized to arbitrary Tychonoff spaces by using maximal filters of zero sets instead of ultrafilters. (Filters of closed sets suffice if the space is normal.)
of C0(X).
 is locally compact, e.g.
is locally compact, e.g.  or
or  , the image of
, the image of  forms an open subset of
forms an open subset of  , or indeed of any compactification, (this is also a necessary condition, as an open subset of a compact Hausdorff space is locally compact). In this case one often studies the remainder of the space,
, or indeed of any compactification, (this is also a necessary condition, as an open subset of a compact Hausdorff space is locally compact). In this case one often studies the remainder of the space, 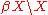 . This is a closed subset of
. This is a closed subset of 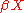 , and so is compact. We consider
, and so is compact. We consider  with its discrete topology and write
with its discrete topology and write  (but this does not appear to be standard notation for general
(but this does not appear to be standard notation for general  ).
).
One can view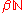 as the set of ultrafilter
as the set of ultrafilter
s on , with the topology generated by sets of the form
, with the topology generated by sets of the form  for
for  .
.  corresponds to the set of principal ultrafilter
corresponds to the set of principal ultrafilter
s, and to the set of free ultrafilters
to the set of free ultrafilters
.
The easiest way to see this is isomorphic to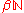 is to show that it satisfies the universal property. For
is to show that it satisfies the universal property. For 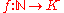 with
with  compact Hausdorff and
compact Hausdorff and  an ultrafilter on
an ultrafilter on  we have an ultrafilter
we have an ultrafilter 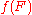 on
on  , the pushforward of
, the pushforward of  . This has a unique limit, say
. This has a unique limit, say  , because
, because  is compact Hausdorff, and we define
is compact Hausdorff, and we define 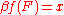 . This may readily be verified to be a continuous extension.
. This may readily be verified to be a continuous extension.
(A similar but slightly more involved construction of the Stone–Čech compactification as a set of certain maximal filters can also be given for a general Tychonoff space .)
.)
The study of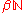 , and in particular
, and in particular  , is a major area of modern set-theoretic topology
, is a major area of modern set-theoretic topology
. The major results motivating this are Parovicenko's theorems, essentially characterising its behaviour under the assumption of the continuum hypothesis
.
These state:
These were originally proved by considering Boolean algebras and applying Stone duality
.
Jan van Mill has described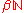 as a 'three headed monster' — the three heads being a smiling and friendly head (the behaviour under the assumption of the continuum hypothesis), the ugly head of independence which constantly tries to confuse you (determining what behaviour is possible in different models of set theory), and the third head is the smallest of all (what you can prove about it in ZFC). It has relatively recently been observed that this characterisation isn't quite right - there is in fact a fourth head of
as a 'three headed monster' — the three heads being a smiling and friendly head (the behaviour under the assumption of the continuum hypothesis), the ugly head of independence which constantly tries to confuse you (determining what behaviour is possible in different models of set theory), and the third head is the smallest of all (what you can prove about it in ZFC). It has relatively recently been observed that this characterisation isn't quite right - there is in fact a fourth head of 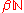 , in which forcing axioms
, in which forcing axioms
and Ramsey type axioms give properties of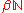 almost diametrically opposed to those under the continuum hypothesis, giving very few maps from
almost diametrically opposed to those under the continuum hypothesis, giving very few maps from  indeed. Examples of these axioms include the combination of Martin's axiom
indeed. Examples of these axioms include the combination of Martin's axiom
and the Open colouring axiom which, for example, prove that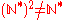 , while the continuum hypothesis implies the opposite.
, while the continuum hypothesis implies the opposite.
 can be used to characterize
can be used to characterize  (the Banach space
(the Banach space
of all bounded sequences in the scalar field R or C, with supremum norm) and its dual space
.
Given a bounded sequence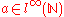 , there exists a closed ball
, there exists a closed ball  that contains the image of
that contains the image of  (
( is a subset of the scalar field).
is a subset of the scalar field).
 is then a function from
is then a function from  to
to  . Since
. Since  is discrete and
is discrete and
 is compact and Hausdorff,
is compact and Hausdorff,
 is continuous. According to the universal property, there exists a unique extension
is continuous. According to the universal property, there exists a unique extension
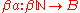 .
.
This extension does not depend on the ball we consider.
we consider.
We have defined an extension map from the space of bounded scalar valued sequences to the space of continuous functions over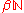 .
.
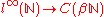
This map is bijective since every function in
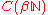 must be bounded and can then be restricted to a bounded scalar sequence.
must be bounded and can then be restricted to a bounded scalar sequence.
If we further consider both spaces with the sup norm the extension map becomes an isometry. Indeed,
if in the construction above we take the smallest possible ball , we see that the sup norm of the extended sequence does not grow (although the image of the extended function can be bigger).
, we see that the sup norm of the extended sequence does not grow (although the image of the extended function can be bigger).
Thus, can be identified with
can be identified with
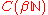 . This allows us to use the Riesz representation theorem
. This allows us to use the Riesz representation theorem
and find that the dual space of
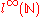 can be identified with the space of finite Borel measures on
can be identified with the space of finite Borel measures on 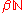 .
.
Finally, it should be noticed that this technique generalizes to the space of an arbitrary measure space
space of an arbitrary measure space  . However, instead of simply considering the space
. However, instead of simply considering the space 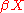 of ultrafilters on
of ultrafilters on  , the right way to generalize this construction is to consider the Stone space
, the right way to generalize this construction is to consider the Stone space  of the measure algebra of
of the measure algebra of  : the spaces
: the spaces 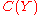 and
and  are isomorphic as C*-algebras as long as
are isomorphic as C*-algebras as long as  satisfies a reasonable finiteness condition (that any set of positive measure contains a subset of finite positive measure).
satisfies a reasonable finiteness condition (that any set of positive measure contains a subset of finite positive measure).
under addition
. It turns out that this operation can be extended (in more than one way) to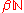 , turning this space also into a monoid, though rather surprisingly a non-commutative one.
, turning this space also into a monoid, though rather surprisingly a non-commutative one.
For any subset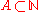 and
and  , we define
, we define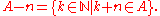
Given two ultrafilters and
and  on
on  , we define their sum by
, we define their sum by
it can be checked that this is again an ultrafilter, and that the operation + is associative (but not commutative) on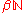 and extends the addition on
and extends the addition on  ; 0 serves as a neutral element for the operation + on
; 0 serves as a neutral element for the operation + on 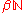 . The operation is also right-continuous, in the sense that for every ultrafilter
. The operation is also right-continuous, in the sense that for every ultrafilter  , the map
, the map
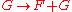
is continuous.
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
βX. The Stone–Čech compactification βX of a topological space X is the largest compact Hausdorff space "generated" by X, in the sense that any map from X to a compact Hausdorff space factors through
βX (in a unique way). If X is a Tychonoff space
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
then the map from X to its image in βX is a homeomorphism, so X can be thought of as a (dense) subspace of βX. For general topological spaces X, the map from X to βX need not be injective.
A form of the axiom of choice is required to prove that every topological space has a Stone–Čech compactification. Even for quite simple spaces
 , an accessible concrete description of
, an accessible concrete description of 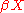 often remains elusive. In particular, proofs that
often remains elusive. In particular, proofs that  is nonempty do not give an explicit description of any particular point in
is nonempty do not give an explicit description of any particular point in 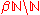 .
.The Stone–Čech compactification was first considered by Tychonoff and later by and .
Universal property and functoriality
βX is a compact Hausdorff space together with a continuous map from X and has the following universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: any continuous map f : X → K, where K is a compact Hausdorff space, lifts uniquely to a continuous map βf : βX → K.
As is usual for universal properties, this universal property, together with the fact that βX is a compact Hausdorff space containing X, characterizes βX up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
.
Some authors add the assumption that the starting space be Tychonoff (or even locally compact Hausdorff), for the following reasons:
- The map from X to its image in βX is a homeomorphism if and only if X is Tychonoff.
- The map from X to its image in βX is a homeomorphism to an open subspace if and only if X is locally compact Hausdorff.
The Stone–Čech construction can be performed for more general spaces X, but the map X → βX need not be a homeomorphism to the image of X (and sometimes is not even injective).
The extension property makes
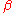 a functor
a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from Top (the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of topological spaces) to CHaus (the category of compact Hausdorff spaces). If we let
 be the inclusion functor from CHaus into Top, maps from
be the inclusion functor from CHaus into Top, maps from 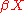 to
to  (for
(for  in CHaus) correspond bijectively to maps from
in CHaus) correspond bijectively to maps from  to
to  (by considering their restriction to
(by considering their restriction to  and using the universal property of
and using the universal property of 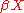 ). i.e.
). i.e. 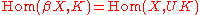 , which means that
, which means that 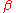 is left adjoint to
is left adjoint to  . This implies that CHaus is a reflective subcategory
. This implies that CHaus is a reflective subcategoryReflective subcategory
In mathematics, a subcategory A of a category B is said to be reflective in B when the inclusion functor from A to B has a left adjoint. This adjoint is sometimes called a reflector...
of Top with reflector
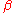 .
.Construction using products
One attempt to construct the Stone–Čech compactification of X is to take the closure of the image of X in
where the product is over all maps from X to compact Hausdorff spaces C. This works intuitively but fails for the technical reason that the collection of all such maps is a proper class rather than a set. There are several ways to modify this idea to make it work; for example, one can restrict the compact Hausdorff spaces C to have underlying set P(P(X)) (the power set of the power set of X), which is sufficiently large that it has cardinality at least equal to that of every compact Hausdorff set to which X can be mapped with dense image.
Construction using the unit interval
One way of constructing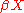 is to consider the map
is to consider the map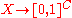
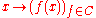
where
 is the set of all continuous function
is the set of all continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s from
 into
into 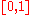 . This may be seen to be a continuous map onto its image, if
. This may be seen to be a continuous map onto its image, if 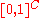 is given the product topology
is given the product topologyProduct topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
. By Tychonoff's theorem
Tychonoff's theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
we have that
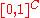 is compact since [0,1] is, so the closure of
is compact since [0,1] is, so the closure of  in
in  is a compactification of
is a compactification of  .
.In order to verify that this is the Stone–Čech compactification, we just need to verify that it satisfies the appropriate universal property. We do this first for
 , where the desired extension of f : X → [0,1] is just the projection onto the
, where the desired extension of f : X → [0,1] is just the projection onto the  coordinate in
coordinate in  . In order to then get this for general compact Hausdorff
. In order to then get this for general compact Hausdorff  we use the above to note that
we use the above to note that  can be embedded in some cube, extend each of the coordinate functions and then take the product of these extensions.
can be embedded in some cube, extend each of the coordinate functions and then take the product of these extensions.The special property of the unit interval needed for this construction to work is that it is a cogenerator of the category of compact Hausdorff spaces: this means that if f and g are any two distinct maps from compact Hausdorff spaces A to B, then there is a map h from B to [0,1] such that hf and hg are distinct. Any other cogenerator (or cogenerating set) can be used in this construction.
Construction using ultrafilters
Alternatively, if is discrete, one can construct
is discrete, one can construct 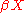 as the set of all ultrafilter
as the set of all ultrafilterUltrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
s on
 , with a topology known as Stone topology. The elements of
, with a topology known as Stone topology. The elements of  correspond to the principal ultrafilter
correspond to the principal ultrafilterUltrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
s.
Again we verify the universal property: For f : X → K with
 compact Hausdorff and
compact Hausdorff and  an ultrafilter on
an ultrafilter on  we have an ultrafilter
we have an ultrafilter 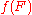 on
on  . This has a unique limit because
. This has a unique limit because  is compact, say
is compact, say  , and we define
, and we define 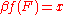 . This may be verified to be a continuous extension of
. This may be verified to be a continuous extension of  .
.Equivalently, one can take the Stone space of the complete Boolean algebra
Complete Boolean algebra
In mathematics, a complete Boolean algebra is a Boolean algebra in which every subset has a supremum . Complete Boolean algebras are used to construct Boolean-valued models of set theory in the theory of forcing...
of all subsets of X as the
Stone–Čech compactification. This is really the same construction, as the Stone space of this Boolean algebra is the set of ultrafilters (or equivalently prime ideals, or homomorphisms to the 2 element Boolean algebra) of the Boolean algebra, which is the same as the set of ultrafilters on X.
The construction can be generalized to arbitrary Tychonoff spaces by using maximal filters of zero sets instead of ultrafilters. (Filters of closed sets suffice if the space is normal.)
Construction using C*-algebras
In case X is a completely regular Hausdorff space, the Stone–Čech compactification can be identified with the spectrum of Cb(X). Here Cb(X) denotes the C*-algebra of all continuous bounded functions on X with sup-norm. Notice that Cb(X) is the multiplier algebraMultiplier algebra
In C*-algebras, the multiplier algebra, denoted by M, of a C*-algebra A is a unital C*-algebra which is the largest unital C*-algebra that contains A as an ideal in a "non-degenerate" way. It is the noncommutative generalization of Stone–Čech compactification...
of C0(X).
The Stone–Čech compactification of the natural numbers
In the case where is locally compact, e.g.
is locally compact, e.g.  or
or  , the image of
, the image of  forms an open subset of
forms an open subset of  , or indeed of any compactification, (this is also a necessary condition, as an open subset of a compact Hausdorff space is locally compact). In this case one often studies the remainder of the space,
, or indeed of any compactification, (this is also a necessary condition, as an open subset of a compact Hausdorff space is locally compact). In this case one often studies the remainder of the space, 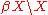 . This is a closed subset of
. This is a closed subset of 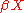 , and so is compact. We consider
, and so is compact. We consider  with its discrete topology and write
with its discrete topology and write  (but this does not appear to be standard notation for general
(but this does not appear to be standard notation for general  ).
).One can view
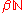 as the set of ultrafilter
as the set of ultrafilterUltrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
s on
 , with the topology generated by sets of the form
, with the topology generated by sets of the form  for
for  .
.  corresponds to the set of principal ultrafilter
corresponds to the set of principal ultrafilterUltrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
s, and
 to the set of free ultrafilters
to the set of free ultrafiltersUltrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
.
The easiest way to see this is isomorphic to
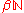 is to show that it satisfies the universal property. For
is to show that it satisfies the universal property. For 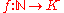 with
with  compact Hausdorff and
compact Hausdorff and  an ultrafilter on
an ultrafilter on  we have an ultrafilter
we have an ultrafilter 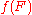 on
on  , the pushforward of
, the pushforward of  . This has a unique limit, say
. This has a unique limit, say  , because
, because  is compact Hausdorff, and we define
is compact Hausdorff, and we define 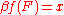 . This may readily be verified to be a continuous extension.
. This may readily be verified to be a continuous extension.(A similar but slightly more involved construction of the Stone–Čech compactification as a set of certain maximal filters can also be given for a general Tychonoff space
 .)
.)The study of
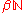 , and in particular
, and in particular  , is a major area of modern set-theoretic topology
, is a major area of modern set-theoretic topologySet-theoretic topology
In mathematics, set-theoretic topology is a subject that combines set theory and general topology. It focuses on topological questions that are independent of ZFC. A famous problem is the normal Moore space question, a question in general topology that was the subject of intense research. The...
. The major results motivating this are Parovicenko's theorems, essentially characterising its behaviour under the assumption of the continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
.
These state:
- Every compact Hausdorff space of weightTopology glossaryThis is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology...
at most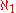 (see Aleph numberAleph numberIn set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
(see Aleph numberAleph numberIn set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
) is the continuous image of (this does not need the continuum hypothesis, but is less interesting in its absence).
(this does not need the continuum hypothesis, but is less interesting in its absence). - If the continuum hypothesis holds then
 is the unique Parovicenko spaceParovicenko spaceIn mathematics, a Parovicenko space is a space similar to the space of non-isolated points of the Stone-Cech compactification of the integers.-Definition:A Parovicenko space is a topological space X satisfying the following conditions:...
is the unique Parovicenko spaceParovicenko spaceIn mathematics, a Parovicenko space is a space similar to the space of non-isolated points of the Stone-Cech compactification of the integers.-Definition:A Parovicenko space is a topological space X satisfying the following conditions:...
, up to isomorphism.
These were originally proved by considering Boolean algebras and applying Stone duality
Stone duality
In mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation...
.
Jan van Mill has described
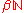 as a 'three headed monster' — the three heads being a smiling and friendly head (the behaviour under the assumption of the continuum hypothesis), the ugly head of independence which constantly tries to confuse you (determining what behaviour is possible in different models of set theory), and the third head is the smallest of all (what you can prove about it in ZFC). It has relatively recently been observed that this characterisation isn't quite right - there is in fact a fourth head of
as a 'three headed monster' — the three heads being a smiling and friendly head (the behaviour under the assumption of the continuum hypothesis), the ugly head of independence which constantly tries to confuse you (determining what behaviour is possible in different models of set theory), and the third head is the smallest of all (what you can prove about it in ZFC). It has relatively recently been observed that this characterisation isn't quite right - there is in fact a fourth head of 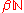 , in which forcing axioms
, in which forcing axiomsForcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...
and Ramsey type axioms give properties of
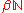 almost diametrically opposed to those under the continuum hypothesis, giving very few maps from
almost diametrically opposed to those under the continuum hypothesis, giving very few maps from  indeed. Examples of these axioms include the combination of Martin's axiom
indeed. Examples of these axioms include the combination of Martin's axiomMartin's axiom
In the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
and the Open colouring axiom which, for example, prove that
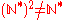 , while the continuum hypothesis implies the opposite.
, while the continuum hypothesis implies the opposite.An application: the dual space of the space of bounded sequences of reals
The Stone–Čech compactification can be used to characterize
can be used to characterize  (the Banach space
(the Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
of all bounded sequences in the scalar field R or C, with supremum norm) and its dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
.
Given a bounded sequence
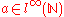 , there exists a closed ball
, there exists a closed ball  that contains the image of
that contains the image of  (
( is a subset of the scalar field).
is a subset of the scalar field). is then a function from
is then a function from  to
to  . Since
. Since  is discrete and
is discrete and is compact and Hausdorff,
is compact and Hausdorff, is continuous. According to the universal property, there exists a unique extension
is continuous. According to the universal property, there exists a unique extension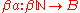 .
.This extension does not depend on the ball
 we consider.
we consider.We have defined an extension map from the space of bounded scalar valued sequences to the space of continuous functions over
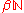 .
.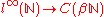
This map is bijective since every function in
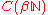 must be bounded and can then be restricted to a bounded scalar sequence.
must be bounded and can then be restricted to a bounded scalar sequence.If we further consider both spaces with the sup norm the extension map becomes an isometry. Indeed,
if in the construction above we take the smallest possible ball
 , we see that the sup norm of the extended sequence does not grow (although the image of the extended function can be bigger).
, we see that the sup norm of the extended sequence does not grow (although the image of the extended function can be bigger).Thus,
 can be identified with
can be identified with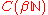 . This allows us to use the Riesz representation theorem
. This allows us to use the Riesz representation theoremRiesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
and find that the dual space of
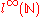 can be identified with the space of finite Borel measures on
can be identified with the space of finite Borel measures on 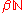 .
.Finally, it should be noticed that this technique generalizes to the
 space of an arbitrary measure space
space of an arbitrary measure space  . However, instead of simply considering the space
. However, instead of simply considering the space 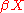 of ultrafilters on
of ultrafilters on  , the right way to generalize this construction is to consider the Stone space
, the right way to generalize this construction is to consider the Stone space  of the measure algebra of
of the measure algebra of  : the spaces
: the spaces 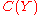 and
and  are isomorphic as C*-algebras as long as
are isomorphic as C*-algebras as long as  satisfies a reasonable finiteness condition (that any set of positive measure contains a subset of finite positive measure).
satisfies a reasonable finiteness condition (that any set of positive measure contains a subset of finite positive measure).Addition on the Stone–Čech compactification of the naturals
The natural numbers form a monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
. It turns out that this operation can be extended (in more than one way) to
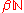 , turning this space also into a monoid, though rather surprisingly a non-commutative one.
, turning this space also into a monoid, though rather surprisingly a non-commutative one.For any subset
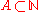 and
and  , we define
, we define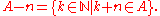
Given two ultrafilters
 and
and  on
on  , we define their sum by
, we define their sum by
it can be checked that this is again an ultrafilter, and that the operation + is associative (but not commutative) on
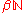 and extends the addition on
and extends the addition on  ; 0 serves as a neutral element for the operation + on
; 0 serves as a neutral element for the operation + on 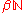 . The operation is also right-continuous, in the sense that for every ultrafilter
. The operation is also right-continuous, in the sense that for every ultrafilter  , the map
, the map
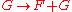
is continuous.
See also
- One-point compactification
- Wallman compactificationWallman compactificationIn mathematics, the Wallman compactification is a compactification of T1 topological spaces that was constructed by .The points of the Wallman compactification ωX of a space X are the maximal families Φ of closed nonempty subsets of X such that Φ is closed under finite intersections...
- Corona setCorona setIn mathematics, the corona or corona set of a topological space X is the complement βX\X of the space in its Stone–Čech compactification βX....
of a space, the complement of its image in the Stone–Čech compactification.
External links
- Dror Bar-Natan, Ultrafilters, Compactness, and the Stone–Čech compactification

