Topology glossary
Encyclopedia
This is a glossary of some terms used in the branch of mathematics
known as topology
. Although there is no absolute distinction between different areas of topology, the focus here is on general topology
. The following definitions are also fundamental to algebraic topology
, differential topology
and geometric topology
.
See the article on topological space
s for basic definitions and examples, and see the article on topology
for a brief history and description of the subject area. See Naive set theory
, Axiomatic set theory, and Function
for definitions concerning sets and functions. The following articles may also be useful. These either contain specialised vocabulary within general topology or provide more detailed expositions of the definitions given below. The list of general topology topics and the list of examples in general topology will also be very helpful.
All spaces in this glossary are assumed to be topological space
s unless stated otherwise.
.
Accumulation point: See limit point
.
Alexandrov topology
: A space X has the Alexandrov topology
(or is finitely generated) if arbitrary intersections of open sets in X are open, or equivalently, if arbitrary unions of closed sets are closed.
Almost discrete: A space is almost discrete if every open set is closed (hence clopen). The almost discrete spaces are precisely the finitely generated zero-dimensional spaces.
Approach space
: An approach space
is a generalization of metric space based on point-to-set distances, instead of point-to-point.
Base
: A collection B of open sets is a base
(or basis) for a topology
if every open set in 
is a union of sets in 
. The topology 
is the smallest topology on 
containing 
and is said to be generated by 
.
Basis: See Base
.
Borel algebra
: The Borel algebra
on a topological space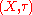
is the smallest 
-algebra
containing all the open sets. It is obtained by taking intersection of all
-algebras on 
containing 
.
Borel set: A Borel set is an element of a Borel algebra.
Boundary
: The boundary
(or frontier) of a set is the set's closure minus its interior. Equivalently, the boundary of a set is the intersection of its closure with the closure of its complement. Boundary of a set
is denoted by 
or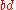 
.
Bounded: A set in a metric space is bounded
if it has finite diameter. Equivalently, a set is bounded if it is contained in some open ball of finite radius. A function
taking values in a metric space is bounded
if its image is a bounded set.
: The category
Top
has topological space
s as objects and continuous maps as morphism
s.
Cauchy sequence
: A sequence
{xn} in a metric space (M, d) is a Cauchy sequence
if, for every positive real number
r, there is an integer
N such that for all integers m, n > N, we have d(xm, xn) < r.
Clopen set
: A set is clopen
if it is both open and closed.
Closed ball: If (M, d) is a metric space
, a closed ball is a set of the form D(x; r) := {y in M : d(x, y) ≤ r}, where x is in M and r is a positive real number
, the radius of the ball. A closed ball of radius r is a closed r-ball. Every closed ball is a closed set in the topology induced on M by d. Note that the closed ball D(x; r) might not be equal to the closure
of the open ball B(x; r).
Closed set
: A set is closed
if its complement is a member of the topology.
Closed function: A function from one space to another is closed if the image
of every closed set is closed.
Closure
: The closure
of a set is the smallest closed set containing the original set. It is equal to the intersection of all closed sets which contain it. An element of the closure of a set S is a point of closure of S.
Closure operator: See Kuratowski closure axioms
.
Coarser topology: If X is a set, and if T1 and T2 are topologies on X, then T1 is coarser (or smaller, weaker) than T2 if T1 is contained in T2. Beware, some authors, especially analyst
s, use the term stronger.
Comeagre: A subset A of a space X is comeagre (comeager) if its complement
X\A is meagre
. Also called residual.
Compact
: A space is compact
if every open cover has a finite subcover. Every compact space is Lindelöf and paracompact. Therefore, every compact Hausdorff space
is normal. See also quasicompact.
Compact-open topology
: The compact-open topology
on the set C(X, Y) of all continuous maps between two spaces X and Y is defined as follows: given a compact subset K of X and an open subset U of Y, let V(K, U) denote the set of all maps f in C(X, Y) such that f(K) is contained in U. Then the collection of all such V(K, U) is a subbase for the compact-open topology.
Complete
: A metric space is complete
if every Cauchy sequence converges.
Completely metrizable/completely metrisable: See complete space
.
Completely normal: A space is completely normal if any two separated sets have disjoint neighbourhoods.
Completely normal Hausdorff: A completely normal Hausdorff space (or T5 space) is a completely normal T1 space. (A completely normal space is Hausdorff if and only if
it is T1, so the terminology is consistent.) Every completely normal Hausdorff space is normal Hausdorff.
Completely regular: A space is completely regular if, whenever C is a closed set and x is a point not in C, then C and {x} are functionally separated.
Completely T3: See Tychonoff
.
Component: See Connected component
/Path-connected component.
Connected: A space is connected if it is not the union of a pair of disjoint nonempty open sets. Equivalently, a space is connected if the only clopen sets are the whole space and the empty set.
Connected component
: A connected component
of a space is a maximal
nonempty connected subspace. Each connected component is closed, and the set of connected components of a space is a partition
of that space.
Continuous: A function from one space to another is continuous if the preimage of every open set is open.
Continuum: A space is called a continuum if it a compact, connected Hausdorff space.
Contractible
: A space X is contractible if the identity map
on X is homotopic to a constant map. Every contractible space is simply connected.
Coproduct topology: If {Xi} is a collection of spaces and X is the (set-theoretic) disjoint union
of {Xi}, then the coproduct topology (or disjoint union topology, topological sum of the Xi) on X is the finest topology for which all the injection maps are continuous.
Countable chain condition
: A space X satisfies the countable chain condition if every family of non-empty, pairswise disjoint open sets is countable.
Countably compact: A space is countably compact if every countable open cover has a finite subcover. Every countably compact space is pseudocompact and weakly countably compact.
Countably locally finite: A collection of subsets of a space X is countably locally finite (or σ-locally finite) if it is the union of a countable collection of locally finite collections of subsets of X.
Cover
: A collection of subsets of a space is a cover (or covering) of that space if the union of the collection is the whole space.
Covering: See Cover.
Cut point: If X is a connected space with more than one point, then a point x of X is a cut point if the subspace X − {x} is disconnected.
: A set is dense if it has nonempty intersection with every nonempty open set. Equivalently, a set is dense if its closure is the whole space.
Derived set: If X is a space and S is a subset of X, the derived set of S in X is the set of limit points of S in X.
Diameter: If (M, d) is a metric space and S is a subset of M, the diameter of S is the supremum
of the distances d(x, y), where x and y range over S.
Discrete metric: The discrete metric on a set X is the function d : X × X → R
such that for all x, y in X, d(x, x) = 0 and d(x, y) = 1 if x ≠ y. The discrete metric induces the discrete topology on X.
Discrete space
: A space X is discrete
if every subset of X is open. We say that X carries the discrete topology.
Discrete topology: See discrete space
.
Disjoint union topology: See Coproduct topology.
Dispersion point
: If X is a connected space with more than one point, then a point x of X is a dispersion point if the subspace X − {x} is hereditarily disconnected (its only connected components are the one-point sets).
Distance: See metric space
.
Dunce hat (topology)
.
Exterior: The exterior of a set is the interior of its complement.
: An Fσ set
is a countable union of closed sets.
Filter
: A filter on a space X is a nonempty family F of subsets of X such that the following conditions hold:
Finer topology: If X is a set, and if T1 and T2 are topologies on X, then T2 is finer (or larger, stronger) than T1 if T2 contains T1. Beware, some authors, especially analyst
s, use the term weaker.
Finitely generated: See Alexandrov topology
.
First category: See Meagre
.
First-countable
: A space is first-countable
if every point has a countable local base.
Fréchet: See T1.
Frontier: See Boundary
.
Full set: A compact
subset K of the complex plane
is called full if its complement
is connected. For example, the closed unit disk is full, while the unit circle
is not.
Functionally separated: Two sets A and B in a space X are functionally separated if there is a continuous map f: X → [0, 1] such that f(A) = 0 and f(B) = 1.
: A Gδ set
is a countable intersection of open sets.
: A Hausdorff space
(or T2 space) is one in which every two distinct points have disjoint neighbourhoods. Every Hausdorff space is T1.
H-closed: A space is H-closed if it is closed in every Hausdorff space containing it.
Hereditary
: A property of spaces is said to be hereditary if whenever a space has that property, then so does every subspace of it. For example, second-countability is a hereditary property.
Homeomorphism
: If X and Y are spaces, a homeomorphism
from X to Y is a bijective
function f : X → Y such that f and f−1 are continuous. The spaces X and Y are then said to be homeomorphic. From the standpoint of topology, homeomorphic spaces are identical.
Homogeneous
: A space X is homogeneous
if, for every x and y in X, there is a homeomorphism f : X → X such that f(x) = y. Intuitively, the space looks the same at every point. Every topological group
is homogeneous.
Homotopic maps: Two continuous maps f, g : X → Y are homotopic (in Y) if there is a continuous map H : X × [0, 1] → Y such that H(x, 0) = f(x) and H(x, 1) = g(x) for all x in X. Here, X × [0, 1] is given the product topology. The function H is called a homotopy (in Y) between f and g.
Homotopy: See Homotopic maps.
Hyper-connected
: A space is hyper-connected if no two non-empty open sets are disjoint. Every hyper-connected space is connected.
Identification space
: See Quotient space
.
Indiscrete space: See Trivial topology
.
Infinite-dimensional topology: See Hilbert manifold
and Q-manifolds, i.e. (generalized) manifolds modelled on the Hilbert space and on the Hilbert cube respectively.
Interior
: The interior
of a set is the largest open set contained in the original set. It is equal to the union of all open sets contained in it. An element of the interior of a set S is an interior point of S.
Interior point: See Interior
.
Isolated point
: A point x is an isolated point
if the singleton {x} is open. More generally, if S is a subset of a space X, and if x is a point of S, then x is an isolated point of S if {x} is open in the subspace topology on S.
Isometric isomorphism: If M1 and M2 are metric spaces, an isometric isomorphism from M1 to M2 is a bijective
isometry f : M1 → M2. The metric spaces are then said to be isometrically isomorphic. From the standpoint of metric space theory, isometrically isomorphic spaces are identical.
Isometry: If (M1, d1) and (M2, d2) are metric spaces, an isometry from M1 to M2 is a function f : M1 → M2 such that d2(f(x), f(y)) = d1(x, y) for all x, y in M1. Every isometry is injective
, although not every isometry is surjective.
: See T0.
Kuratowski closure axioms
: The Kuratowski closure axioms
is a set of axiom
s satisfied by the function which takes each subset of X to its closure:
Limit point
: A point x in a space X is a limit point
of a subset S if every open set containing x also contains a point of S other than x itself. This is equivalent to requiring that every neighbourhood of x contains a point of S other than x itself.
Limit point compact: See Weakly countably compact.
Lindelöf
: A space is Lindelöf
if every open cover has a countable subcover.
Local base: A set B of neighbourhoods of a point x of a space X is a local base (or local basis, neighbourhood base, neighbourhood basis) at x if every neighbourhood of x contains some member of B.
Local basis: See Local base.
Locally closed subset: A subset of a topological space that is the intersection of an open and a closed subset. Equivalently, it is a relatively open subset of its closure.
Locally compact
: A space is locally compact
if every point has a local base consisting of compact neighbourhoods. Every locally compact Hausdorff space is Tychonoff.
Locally connected: A space is locally connected if every point has a local base consisting of connected neighbourhoods.
Locally finite: A collection of subsets of a space is locally finite if every point has a neighbourhood which has nonempty intersection with only finitely many of the subsets. See also countably locally finite, point finite.
Locally metrizable/Locally metrisable: A space is locally metrizable if every point has a metrizable neighbourhood.
Locally path-connected: A space is locally path-connected if every point has a local base consisting of path-connected neighbourhoods. A locally path-connected space is connected if and only if
it is path-connected.
Locally simply connected: A space is locally simply connected if every point has a local base consisting of simply connected neighbourhoods.
Loop
: If x is a point in a space X, a loop
at x in X (or a loop in X with basepoint x) is a path f in X, such that f(0) = f(1) = x. Equivalently, a loop in X is a continuous map from the unit circle
S1 into X.
: If X is a space and A is a subset of X, then A is meagre in X (or of first category in X) if it is the countable union of nowhere dense sets. If A is not meagre in X, A is of second category in X.
Metric: See Metric space
.
Metric invariant: A metric invariant is a property which is preserved under isometric isomorphism.
Metric map: If X and Y are metric spaces with metrics dX and dY respectively, then a metric map is a function f from X to Y, such that for any points x and y in X, dY(f(x), f(y)) ≤ dX(x, y). A metric map is strictly metric if the above inequality is strict for all x and y in X.
Metric space
: A metric space
(M, d) is a set M equipped with a function d : M × M → R
satisfying the following axioms for all x, y, and z in M:
Metrizable/Metrisable: A space is metrizable if it is homeomorphic to a metric space. Every metrizable space is Hausdorff and paracompact (and hence normal and Tychonoff). Every metrizable space is first-countable.
Monolith: Every non-empty ultra-connected compact space X has a largest proper open subset; this subset is called a monolith.
/Neighborhood: A neighbourhood of a point x is a set containing an open set which in turn contains the point x. More generally, a neighbourhood of a set S is a set containing an open set which in turn contains the set S. A neighbourhood of a point x is thus a neighbourhood of the singleton set {x}. (Note that under this definition, the neighbourhood itself need not be open. Many authors require that neighbourhoods be open; be careful to note conventions.)
Neighbourhood base/basis: See Local base.
Neighbourhood system for a point x: A neighbourhood system at a point x in a space is the collection of all neighbourhoods of x.
Net
: A net
in a space X is a map from a directed set
A to X. A net from A to X is usually denoted (xα), where α is an index variable
ranging over A. Every sequence
is a net, taking A to be the directed set of natural number
s with the usual ordering.
Normal
: A space is normal
if any two disjoint closed sets have disjoint neighbourhoods. Every normal space admits a partition of unity.
Normal Hausdorff: A normal Hausdorff space (or T4 space) is a normal T1 space. (A normal space is Hausdorff if and only if
it is T1, so the terminology is consistent.) Every normal Hausdorff space is Tychonoff.
Nowhere dense
: A nowhere dense set
is a set whose closure has empty interior.
Open ball: If (M, d) is a metric space, an open ball is a set of the form B(x; r) := {y in M : d(x, y) < r}, where x is in M and r is a positive real number
, the radius of the ball. An open ball of radius r is an open r-ball. Every open ball is an open set in the topology on M induced by d.
Open condition: See open property.
Open set
: An open set
is a member of the topology.
Open function: A function from one space to another is open if the image
of every open set is open.
Open property: A property of points in a topological space
is said to be "open" if those points which possess it form an open set
. Such conditions often take a common form, and that form can be said to be an open condition; for example, in metric space
s, one defines an open ball as above, and says that "strict inequality is an open condition".
: A space is paracompact
if every open cover has a locally finite open refinement. Paracompact Hausdorff spaces are normal.
Partition of unity: A partition of unity of a space X is a set of continuous functions from X to [0, 1] such that any point has a neighbourhood where all but a finite number of the functions are identically zero, and the sum of all the functions on the entire space is identically 1.
Path
: A path
in a space X is a continuous map f from the closed unit interval
[0, 1] into X. The point f(0) is the initial point of f; the point f(1) is the terminal point of f.
Path-connected: A space X is path-connected if, for every two points x, y in X, there is a path f from x to y, i.e., a path with initial point f(0) = x and terminal point f(1) = y. Every path-connected space is connected.
Path-connected component: A path-connected component of a space is a maximal nonempty path-connected subspace. The set of path-connected components of a space is a partition
of that space, which is finer
than the partition into connected components. The set of path-connected components of a space X is denoted π0(X).
π-base: A collection B of nonempty open sets is a π-base for a topology τ if every nonempty open set in τ includes a set from B.
Point: A point is an element of a topological space. More generally, a point is an element of any set with an underlying topological structure; e.g. an element of a metric space or a topological group is also a "point".
Point of closure: See Closure
.
Polish
: A space is Polish if it is separable and topologically complete, i.e. if it is homeomorphic to a separable and complete metric space.
P-point: A point of a topological space is a P-point if its filter of neighbourhoods is closed under countable intersections.
Pre-compact: See Relatively compact.
Product topology
: If {Xi} is a collection of spaces and X is the (set-theoretic) product
of {Xi}, then the product topology
on X is the coarsest topology for which all the projection maps are continuous.
Proper function/mapping: A continuous function f from a space X to a space Y is proper if f−1(C) is a compact set in X for any compact subspace C of Y.
Proximity space
: A proximity space (X, δ) is a set X equipped with a binary relation
δ between subsets of X satisfying the following properties:
Pseudocompact: A space is pseudocompact if every real-valued
continuous function on the space is bounded.
Pseudometric: See Pseudometric space.
Pseudometric space: A pseudometric space (M, d) is a set M equipped with a function d : M × M → R
satisfying all the conditions of a metric space, except possibly the identity of indiscernibles. That is, points in a pseudometric space may be "infinitely close" without being identical. The function d is a pseudometric on M. Every metric is a pseudometric.
Punctured neighbourhood/Punctured neighborhood: A punctured neighbourhood of a point x is a neighbourhood of x, minus {x}. For instance, the interval
(−1, 1) = {y : −1 < y < 1} is a neighbourhood of x = 0 in the real line
, so the set (−1, 0) ∪ (0, 1) = (−1, 1) − {0} is a punctured neighbourhood of 0.
. Some authors define "compact" to include the Hausdorff
separation axiom, and they use the term quasicompact to mean what we call in this glossary simply "compact" (without the Hausdorff axiom). This convention is most commonly found in French, and branches of mathematics heavily influenced by the French.
Quotient map: If X and Y are spaces, and if f is a surjection from X to Y, then f is a quotient map (or identification map) if, for every subset U of Y, U is open in Y if and only if
f -1(U) is open in X. In other words, Y has the f-strong topology. Equivalently,
is a quotient map if and only if it is the transfinite composition of maps 
, where 
is a subset. Note that this doesn't imply that f is an open function.
Quotient space
: If X is a space, Y is a set, and f : X → Y is any surjective function, then the quotient topology
on Y induced by f is the finest topology for which f is continuous. The space X is a quotient space or identification space. By definition, f is a quotient map. The most common example of this is to consider an equivalence relation
on X, with Y the set of equivalence classes and f the natural projection map. This construction is dual to the construction of the subspace topology.
Regular
: A space is regular
if, whenever C is a closed set and x is a point not in C, then C and x have disjoint neighbourhoods.
Regular Hausdorff: A space is regular Hausdorff (or T3) if it is a regular T0 space. (A regular space is Hausdorff if and only if
it is T0, so the terminology is consistent.)
Regular open: An open subset U of a space X is regular open if it equals the interior of its closure. An example of a non-regular open set is the set U = (0, 1) U (1, 2) in R with its normal topology, since 1 is in the interior of the closure of U, but not in U. The regular open subsets of a space form a complete Boolean algebra
.
Relatively compact: A subset Y of a space X is relatively compact in X if the closure of Y in X is compact.
Residual: If X is a space and A is a subset of X, then A is residual in X if the complement of A is meagre in X. Also called comeagre or comeager.
Resolvable: A topological space
is called resolvable
if it is expressible as the union of two disjoint dense subsets.
Rim-compact: A space is rim-compact if it has a base of open sets whose boundaries are compact.
Second-countable
: A space is second-countable
if it has a countable base for its topology. Every second-countable space is first-countable, separable, and Lindelöf.
Semilocally simply connected: A space X is semilocally simply connected if, for every point x in X, there is a neighbourhood U of x such that every loop at x in U is homotopic in X to the constant loop x. Every simply connected space and every locally simply connected space is semilocally simply connected. (Compare with locally simply connected; here, the homotopy is allowed to live in X, whereas in the definition of locally simply connected, the homotopy must live in U.)
Semiregular
: A space is semiregular if the regular open sets form a base.
Separable: A space is separable if it has a countable dense subset.
Separated
: Two sets A and B are separated
if each is disjoint from the other's closure.
Sequentially compact: A space is sequentially compact if every sequence
has a convergent subsequence. Every sequentially compact space is countably compact, and every first-countable, countably compact space is sequentially compact.
Short map
: See metric map
Simply connected
: A space is simply connected
if it is path-connected and every loop is homotopic to a constant map.
Smaller topology: See Coarser topology.
Star: The star of a point in a given cover
of a topological space
is the union of all the sets in the cover that contain the point. See star refinement
.
-Strong topology: Let 
be a map of topological spaces. We say that 
has the 
-strong topology if, for every subset 
, one has that 
is open in 
if and only if 
is open in 
Stronger topology: See Finer topology. Beware, some authors, especially analyst
s, use the term weaker topology.
Subbase
: A collection of open sets is a subbase
(or subbasis) for a topology if every non-empty proper open set in the topology is a union of finite intersections of sets in the subbase. If B is any collection of subsets of a set X, the topology on X generated by B is the smallest topology containing B; this topology consists of the empty set, X and all unions of finite intersections of elements of B.
Subbasis
: See Subbase
.
Subcover: A cover K is a subcover (or subcovering) of a cover L if every member of K is a member of L.
Subcovering: See Subcover.
Submaximal space: A topological space
is said to be submaximal if every subset of it is locally closed, that is, every subset is the intersection of an open set
and a closed set
.
Here are some facts about submaximality as a property of topological spaces:
Subspace: If T is a topology on a space X, and if A is a subset of X, then the subspace topology
on A induced by T consists of all intersections of open sets in T with A. This construction is dual to the construction of the quotient topology.
T1
: A space is T1
(or Fréchet or accessible) if for every pair of distinct points x and y in the space, there is an open set containing x but not y. (Compare with T0; here, we are allowed to specify which point will be contained in the open set.) Equivalently, a space is T1 if all its singletons are closed. Every T1 space is T0.
T2: See Hausdorff space
.
T3: See Regular Hausdorff.
T3½
: See Tychonoff space
.
T4: See Normal Hausdorff.
T5: See Completely normal Hausdorff.
Top
: See Category of topological spaces
.
Topological invariant: A topological invariant is a property which is preserved under homeomorphism. For example, compactness and connectedness are topological properties, whereas boundedness and completeness are not. Algebraic topology
is the study of topologically invariant abstract algebra
constructions on topological spaces.
Topological space
: A topological space
(X, T) is a set X equipped with a collection T of subsets of X satisfying the following axiom
s:
Topological sum: See Coproduct topology.
Topologically complete
: A space is topologically complete
if it is homeomorphic to a complete metric space.
Topology: See Topological space
.
Totally bounded: A metric space M is totally bounded if, for every r > 0, there exist a finite cover of M by open balls of radius r. A metric space is compact if and only if it is complete and totally bounded.
Totally disconnected: A space is totally disconnected if it has no connected subset with more than one point.
Trivial topology
: The trivial topology
(or indiscrete topology) on a set X consists of precisely the empty set and the entire space X.
Tychonoff
: A Tychonoff space
(or completely regular Hausdorff space, completely T3 space, T3.5 space) is a completely regular T0 space. (A completely regular space is Hausdorff if and only if
it is T0, so the terminology is consistent.) Every Tychonoff space is regular Hausdorff.
Ultrametric: A metric is an ultrametric if it satisfies the following stronger version of the triangle inequality: for all x, y, z in M, d(x, z) ≤ max(d(x, y), d(y, z)).
Uniform isomorphism
: If X and Y are uniform space
s, a uniform isomorphism from X to Y is a bijective function f : X → Y such that f and f−1 are uniformly continuous. The spaces are then said to be uniformly isomorphic and share the same uniform properties.
Uniformizable/Uniformisable: A space is uniformizable if it is homeomorphic to a uniform space.
Uniform space
: A uniform space
is a set U equipped with a nonempty collection Φ of subsets of the Cartesian product
X × X satisfying the following axiom
s:
Uniform structure: See Uniform space
.
: The weak topology
on a set, with respect to a collection of functions from that set into topological spaces, is the coarsest topology on the set which makes all the functions continuous.
Weaker topology: See Coarser topology. Beware, some authors, especially analyst
s, use the term stronger topology.
Weakly countably compact: A space is weakly countably compact (or limit point compact) if every infinite subset has a limit point.
Weakly hereditary: A property of spaces is said to be weakly hereditary if whenever a space has that property, then so does every closed subspace of it. For example, compactness and the Lindelöf property are both weakly hereditary properties, although neither is hereditary.
Weight: The weight of a space X is the smallest cardinal number
κ such that X has a base of cardinal κ. (Note that such a cardinal number exists, because the entire topology forms a base, and because the class of cardinal numbers is well-ordered.)
Well-connected: See Ultra-connected. (Some authors use this term strictly for ultra-connected compact spaces.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
known as topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. Although there is no absolute distinction between different areas of topology, the focus here is on general topology
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
. The following definitions are also fundamental to algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
and geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
.
See the article on topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s for basic definitions and examples, and see the article on topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
for a brief history and description of the subject area. See Naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
, Axiomatic set theory, and Function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
for definitions concerning sets and functions. The following articles may also be useful. These either contain specialised vocabulary within general topology or provide more detailed expositions of the definitions given below. The list of general topology topics and the list of examples in general topology will also be very helpful.
- Compact spaceCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
- Connected spaceConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
- Continuity
- Metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
- Separated setsSeparated setsIn topology and related branches of mathematics, separated sets are pairs of subsets of a given topological space that are related to each other in a certain way....
- Separation axiomSeparation axiomIn topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
- Topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
- Uniform spaceUniform spaceIn the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
All spaces in this glossary are assumed to be topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s unless stated otherwise.
A
Accessible: SeeT1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
.
Accumulation point: See limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
.
Alexandrov topology
Alexandrov topology
In topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
: A space X has the Alexandrov topology
Alexandrov topology
In topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
(or is finitely generated) if arbitrary intersections of open sets in X are open, or equivalently, if arbitrary unions of closed sets are closed.
Almost discrete: A space is almost discrete if every open set is closed (hence clopen). The almost discrete spaces are precisely the finitely generated zero-dimensional spaces.
Approach space
Approach space
In topology, approach spaces are a generalization of metric spaces, based on point-to-set distances, instead of point-to-point distances. They were introduced by in 1989.-Definition:...
: An approach space
Approach space
In topology, approach spaces are a generalization of metric spaces, based on point-to-set distances, instead of point-to-point distances. They were introduced by in 1989.-Definition:...
is a generalization of metric space based on point-to-set distances, instead of point-to-point.
B
Baire space: This has two distinct common meanings:-
- A space is a Baire space if the intersection of any countable collection of dense open sets is dense; see Baire spaceBaire spaceIn mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
. - Baire space is the set of all functions from the natural numbers to the natural numbers, with the topology of pointwise convergence; see Baire space (set theory)Baire space (set theory)In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is often denoted B, N'N, or ωω...
.
- A space is a Baire space if the intersection of any countable collection of dense open sets is dense; see Baire space
Base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
: A collection B of open sets is a base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
(or basis) for a topology
if every open set in is a union of sets in . The topology is the smallest topology on containing and is said to be generated by .Basis: See Base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
.
Borel algebra
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
: The Borel algebra
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
on a topological space
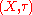is the smallest -algebraSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
containing all the open sets. It is obtained by taking intersection of all
-algebras on containing .Borel set: A Borel set is an element of a Borel algebra.
Boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
: The boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
(or frontier) of a set is the set's closure minus its interior. Equivalently, the boundary of a set is the intersection of its closure with the closure of its complement. Boundary of a set
is denoted by or 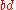.Bounded: A set in a metric space is bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
if it has finite diameter. Equivalently, a set is bounded if it is contained in some open ball of finite radius. A function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
taking values in a metric space is bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
if its image is a bounded set.
C
Category of topological spacesCategory of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
: The category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
Top
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
has topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s as objects and continuous maps as morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s.
Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
: A sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
{xn} in a metric space (M, d) is a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
if, for every positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
r, there is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
N such that for all integers m, n > N, we have d(xm, xn) < r.
Clopen set
Clopen set
In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
: A set is clopen
Clopen set
In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
if it is both open and closed.
Closed ball: If (M, d) is a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, a closed ball is a set of the form D(x; r) := {y in M : d(x, y) ≤ r}, where x is in M and r is a positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, the radius of the ball. A closed ball of radius r is a closed r-ball. Every closed ball is a closed set in the topology induced on M by d. Note that the closed ball D(x; r) might not be equal to the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the open ball B(x; r).
Closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
: A set is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
if its complement is a member of the topology.
Closed function: A function from one space to another is closed if the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of every closed set is closed.
Closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
: The closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of a set is the smallest closed set containing the original set. It is equal to the intersection of all closed sets which contain it. An element of the closure of a set S is a point of closure of S.
Closure operator: See Kuratowski closure axioms
Kuratowski closure axioms
In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition...
.
Coarser topology: If X is a set, and if T1 and T2 are topologies on X, then T1 is coarser (or smaller, weaker) than T2 if T1 is contained in T2. Beware, some authors, especially analyst
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
s, use the term stronger.
Comeagre: A subset A of a space X is comeagre (comeager) if its complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
X\A is meagre
Meagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
. Also called residual.
Compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
: A space is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
if every open cover has a finite subcover. Every compact space is Lindelöf and paracompact. Therefore, every compact Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is normal. See also quasicompact.
Compact-open topology
Compact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
: The compact-open topology
Compact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
on the set C(X, Y) of all continuous maps between two spaces X and Y is defined as follows: given a compact subset K of X and an open subset U of Y, let V(K, U) denote the set of all maps f in C(X, Y) such that f(K) is contained in U. Then the collection of all such V(K, U) is a subbase for the compact-open topology.
Complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
: A metric space is complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
if every Cauchy sequence converges.
Completely metrizable/completely metrisable: See complete space
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
.
Completely normal: A space is completely normal if any two separated sets have disjoint neighbourhoods.
Completely normal Hausdorff: A completely normal Hausdorff space (or T5 space) is a completely normal T1 space. (A completely normal space is Hausdorff if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is T1, so the terminology is consistent.) Every completely normal Hausdorff space is normal Hausdorff.
Completely regular: A space is completely regular if, whenever C is a closed set and x is a point not in C, then C and {x} are functionally separated.
Completely T3: See Tychonoff
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
.
Component: See Connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
/Path-connected component.
Connected: A space is connected if it is not the union of a pair of disjoint nonempty open sets. Equivalently, a space is connected if the only clopen sets are the whole space and the empty set.
Connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
: A connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
of a space is a maximal
Maximal
Maximal may refer to:*Maximal element, a mathematical definition*Maximal , a faction of Transformers*Maximalism, an artistic style*Maximal set*Maxim , a men's magazine marketed as Maximal in several countriesSee also...
nonempty connected subspace. Each connected component is closed, and the set of connected components of a space is a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of that space.
Continuous: A function from one space to another is continuous if the preimage of every open set is open.
Continuum: A space is called a continuum if it a compact, connected Hausdorff space.
Contractible
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
: A space X is contractible if the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on X is homotopic to a constant map. Every contractible space is simply connected.
Coproduct topology: If {Xi} is a collection of spaces and X is the (set-theoretic) disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of {Xi}, then the coproduct topology (or disjoint union topology, topological sum of the Xi) on X is the finest topology for which all the injection maps are continuous.
Countable chain condition
Countable chain condition
In order theory, a partially ordered set X is said to satisfy the countable chain condition, or to be ccc, if every strong antichain in X is countable. There are really two conditions: the upwards and downwards countable chain conditions. These are not equivalent...
: A space X satisfies the countable chain condition if every family of non-empty, pairswise disjoint open sets is countable.
Countably compact: A space is countably compact if every countable open cover has a finite subcover. Every countably compact space is pseudocompact and weakly countably compact.
Countably locally finite: A collection of subsets of a space X is countably locally finite (or σ-locally finite) if it is the union of a countable collection of locally finite collections of subsets of X.
Cover
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
: A collection of subsets of a space is a cover (or covering) of that space if the union of the collection is the whole space.
Covering: See Cover.
Cut point: If X is a connected space with more than one point, then a point x of X is a cut point if the subspace X − {x} is disconnected.
D
Dense setDense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
: A set is dense if it has nonempty intersection with every nonempty open set. Equivalently, a set is dense if its closure is the whole space.
Derived set: If X is a space and S is a subset of X, the derived set of S in X is the set of limit points of S in X.
Diameter: If (M, d) is a metric space and S is a subset of M, the diameter of S is the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of the distances d(x, y), where x and y range over S.
Discrete metric: The discrete metric on a set X is the function d : X × X → R
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
such that for all x, y in X, d(x, x) = 0 and d(x, y) = 1 if x ≠ y. The discrete metric induces the discrete topology on X.
Discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
: A space X is discrete
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
if every subset of X is open. We say that X carries the discrete topology.
Discrete topology: See discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
.
Disjoint union topology: See Coproduct topology.
Dispersion point
Dispersion point
In topology, a dispersion point or explosion point is a point in a topological space the removal of which leaves the space highly disconnected....
: If X is a connected space with more than one point, then a point x of X is a dispersion point if the subspace X − {x} is hereditarily disconnected (its only connected components are the one-point sets).
Distance: See metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
.
Dunce hat (topology)
Dunce hat (topology)
For the item of clothing designed to be humiliating, now rarely used, see dunce cap.In topology, the dunce hat is a compact topological space formed by taking a solid triangle and gluing all three sides together, with the orientation of one side reversed...
E
Entourage: See Uniform spaceUniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
.
Exterior: The exterior of a set is the interior of its complement.
F
Fσ setF-sigma set
In mathematics, an Fσ set is a countable union of closed sets. The notation originated in France with F for fermé and σ for somme ....
: An Fσ set
F-sigma set
In mathematics, an Fσ set is a countable union of closed sets. The notation originated in France with F for fermé and σ for somme ....
is a countable union of closed sets.
Filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
: A filter on a space X is a nonempty family F of subsets of X such that the following conditions hold:
-
- The empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is not in F. - The intersection of any finite number of elements of F is again in F.
- If A is in F and if B contains A, then B is in F.
- The empty set
Finer topology: If X is a set, and if T1 and T2 are topologies on X, then T2 is finer (or larger, stronger) than T1 if T2 contains T1. Beware, some authors, especially analyst
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
s, use the term weaker.
Finitely generated: See Alexandrov topology
Alexandrov topology
In topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
.
First category: See Meagre
Meagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
.
First-countable
First-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
: A space is first-countable
First-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
if every point has a countable local base.
Fréchet: See T1.
Frontier: See Boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
.
Full set: A compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
subset K of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
is called full if its complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
is connected. For example, the closed unit disk is full, while the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
is not.
Functionally separated: Two sets A and B in a space X are functionally separated if there is a continuous map f: X → [0, 1] such that f(A) = 0 and f(B) = 1.
G
Gδ setG-delta set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
: A Gδ set
G-delta set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
is a countable intersection of open sets.
H
HausdorffHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
: A Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
(or T2 space) is one in which every two distinct points have disjoint neighbourhoods. Every Hausdorff space is T1.
H-closed: A space is H-closed if it is closed in every Hausdorff space containing it.
Hereditary
Hereditary property
In mathematics, a hereditary property is a property of an object, that inherits to all its subobjects, where the term subobject depends on the context. These properties are particularly considered in topology and graph theory.-In topology:...
: A property of spaces is said to be hereditary if whenever a space has that property, then so does every subspace of it. For example, second-countability is a hereditary property.
Homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
: If X and Y are spaces, a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
from X to Y is a bijective
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
function f : X → Y such that f and f−1 are continuous. The spaces X and Y are then said to be homeomorphic. From the standpoint of topology, homeomorphic spaces are identical.
Homogeneous
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
: A space X is homogeneous
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
if, for every x and y in X, there is a homeomorphism f : X → X such that f(x) = y. Intuitively, the space looks the same at every point. Every topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
is homogeneous.
Homotopic maps: Two continuous maps f, g : X → Y are homotopic (in Y) if there is a continuous map H : X × [0, 1] → Y such that H(x, 0) = f(x) and H(x, 1) = g(x) for all x in X. Here, X × [0, 1] is given the product topology. The function H is called a homotopy (in Y) between f and g.
Homotopy: See Homotopic maps.
Hyper-connected
Hyperconnected space
In mathematics, a hyperconnected space is a topological space X that cannot be written as the union of two proper closed sets. The name irreducible space is preferred in algebraic geometry....
: A space is hyper-connected if no two non-empty open sets are disjoint. Every hyper-connected space is connected.
I
Identification map: See Quotient map.Identification space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
: See Quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
.
Indiscrete space: See Trivial topology
Trivial topology
In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
.
Infinite-dimensional topology: See Hilbert manifold
Hilbert manifold
In mathematics, a Hilbert manifold is a manifold modeled on Hilbert spaces. Thus it is a separable Hausdorff space in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space. The concept of a Hilbert manifold provides a possibility of extending the theory of...
and Q-manifolds, i.e. (generalized) manifolds modelled on the Hilbert space and on the Hilbert cube respectively.
Interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
: The interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of a set is the largest open set contained in the original set. It is equal to the union of all open sets contained in it. An element of the interior of a set S is an interior point of S.
Interior point: See Interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
.
Isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
: A point x is an isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
if the singleton {x} is open. More generally, if S is a subset of a space X, and if x is a point of S, then x is an isolated point of S if {x} is open in the subspace topology on S.
Isometric isomorphism: If M1 and M2 are metric spaces, an isometric isomorphism from M1 to M2 is a bijective
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
isometry f : M1 → M2. The metric spaces are then said to be isometrically isomorphic. From the standpoint of metric space theory, isometrically isomorphic spaces are identical.
Isometry: If (M1, d1) and (M2, d2) are metric spaces, an isometry from M1 to M2 is a function f : M1 → M2 such that d2(f(x), f(y)) = d1(x, y) for all x, y in M1. Every isometry is injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
, although not every isometry is surjective.
K
Kolmogorov axiomKolmogorov space
In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
: See T0.
Kuratowski closure axioms
Kuratowski closure axioms
In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition...
: The Kuratowski closure axioms
Kuratowski closure axioms
In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition...
is a set of axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s satisfied by the function which takes each subset of X to its closure:
-
- Isotonicity: Every set is contained in its closure.
- Idempotence: The closure of the closure of a set is equal to the closure of that set.
- Preservation of binary unions: The closure of the union of two sets is the union of their closures.
- Preservation of nullary unions: The closure of the empty set is empty.
- If c is a function from the power set of X to itself, then c is a closure operator if it satisfies the Kuratowski closure axioms. The Kuratowski closure axioms can then be used to define a topology on X by declaring the closed sets to be the fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of this operator, i.e. a set A is closed if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
c(A) = A.
L
Larger topology: See Finer topology.Limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
: A point x in a space X is a limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of a subset S if every open set containing x also contains a point of S other than x itself. This is equivalent to requiring that every neighbourhood of x contains a point of S other than x itself.
Limit point compact: See Weakly countably compact.
Lindelöf
Lindelöf space
In mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
: A space is Lindelöf
Lindelöf space
In mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
if every open cover has a countable subcover.
Local base: A set B of neighbourhoods of a point x of a space X is a local base (or local basis, neighbourhood base, neighbourhood basis) at x if every neighbourhood of x contains some member of B.
Local basis: See Local base.
Locally closed subset: A subset of a topological space that is the intersection of an open and a closed subset. Equivalently, it is a relatively open subset of its closure.
Locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
: A space is locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
if every point has a local base consisting of compact neighbourhoods. Every locally compact Hausdorff space is Tychonoff.
Locally connected: A space is locally connected if every point has a local base consisting of connected neighbourhoods.
Locally finite: A collection of subsets of a space is locally finite if every point has a neighbourhood which has nonempty intersection with only finitely many of the subsets. See also countably locally finite, point finite.
Locally metrizable/Locally metrisable: A space is locally metrizable if every point has a metrizable neighbourhood.
Locally path-connected: A space is locally path-connected if every point has a local base consisting of path-connected neighbourhoods. A locally path-connected space is connected if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is path-connected.
Locally simply connected: A space is locally simply connected if every point has a local base consisting of simply connected neighbourhoods.
Loop
Loop (topology)
In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...
: If x is a point in a space X, a loop
Loop (topology)
In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...
at x in X (or a loop in X with basepoint x) is a path f in X, such that f(0) = f(1) = x. Equivalently, a loop in X is a continuous map from the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
S1 into X.
M
MeagreMeagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
: If X is a space and A is a subset of X, then A is meagre in X (or of first category in X) if it is the countable union of nowhere dense sets. If A is not meagre in X, A is of second category in X.
Metric: See Metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
.
Metric invariant: A metric invariant is a property which is preserved under isometric isomorphism.
Metric map: If X and Y are metric spaces with metrics dX and dY respectively, then a metric map is a function f from X to Y, such that for any points x and y in X, dY(f(x), f(y)) ≤ dX(x, y). A metric map is strictly metric if the above inequality is strict for all x and y in X.
Metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
: A metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(M, d) is a set M equipped with a function d : M × M → R
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
satisfying the following axioms for all x, y, and z in M:
-
- d(x, y) ≥ 0
- d(x, x) = 0
- if d(x, y) = 0 then x = y (identity of indiscernibles)
- d(x, y) = d(y, x) (symmetry)
- d(x, z) ≤ d(x, y) + d(y, z) (triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
)
- The function d is a metric on M, and d(x, y) is the distance between x and y. The collection of all open balls of M is a base for a topology on M; this is the topology on M induced by d. Every metric space is Hausdorff and paracompact (and hence normal and Tychonoff). Every metric space is first-countable.
Metrizable/Metrisable: A space is metrizable if it is homeomorphic to a metric space. Every metrizable space is Hausdorff and paracompact (and hence normal and Tychonoff). Every metrizable space is first-countable.
Monolith: Every non-empty ultra-connected compact space X has a largest proper open subset; this subset is called a monolith.
N
NeighbourhoodNeighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
/Neighborhood: A neighbourhood of a point x is a set containing an open set which in turn contains the point x. More generally, a neighbourhood of a set S is a set containing an open set which in turn contains the set S. A neighbourhood of a point x is thus a neighbourhood of the singleton set {x}. (Note that under this definition, the neighbourhood itself need not be open. Many authors require that neighbourhoods be open; be careful to note conventions.)
Neighbourhood base/basis: See Local base.
Neighbourhood system for a point x: A neighbourhood system at a point x in a space is the collection of all neighbourhoods of x.
Net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
: A net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
in a space X is a map from a directed set
Directed set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
A to X. A net from A to X is usually denoted (xα), where α is an index variable
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
ranging over A. Every sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
is a net, taking A to be the directed set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s with the usual ordering.
Normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
: A space is normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
if any two disjoint closed sets have disjoint neighbourhoods. Every normal space admits a partition of unity.
Normal Hausdorff: A normal Hausdorff space (or T4 space) is a normal T1 space. (A normal space is Hausdorff if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is T1, so the terminology is consistent.) Every normal Hausdorff space is Tychonoff.
Nowhere dense
Nowhere dense set
In mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. The order of operations is important. For example, the set of rational numbers, as a subset of R has the property that the closure of the interior is empty, but it is not nowhere dense; in fact it...
: A nowhere dense set
Nowhere dense set
In mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. The order of operations is important. For example, the set of rational numbers, as a subset of R has the property that the closure of the interior is empty, but it is not nowhere dense; in fact it...
is a set whose closure has empty interior.
O
Open cover: An open cover is a cover consisting of open sets.Open ball: If (M, d) is a metric space, an open ball is a set of the form B(x; r) := {y in M : d(x, y) < r}, where x is in M and r is a positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, the radius of the ball. An open ball of radius r is an open r-ball. Every open ball is an open set in the topology on M induced by d.
Open condition: See open property.
Open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
: An open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
is a member of the topology.
Open function: A function from one space to another is open if the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of every open set is open.
Open property: A property of points in a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is said to be "open" if those points which possess it form an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
. Such conditions often take a common form, and that form can be said to be an open condition; for example, in metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, one defines an open ball as above, and says that "strict inequality is an open condition".
P
ParacompactParacompact space
In mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by ....
: A space is paracompact
Paracompact space
In mathematics, a paracompact space is a topological space in which every open cover admits a locally finite open refinement. Paracompact spaces are sometimes also required to be Hausdorff. Paracompact spaces were introduced by ....
if every open cover has a locally finite open refinement. Paracompact Hausdorff spaces are normal.
Partition of unity: A partition of unity of a space X is a set of continuous functions from X to [0, 1] such that any point has a neighbourhood where all but a finite number of the functions are identically zero, and the sum of all the functions on the entire space is identically 1.
Path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
: A path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
in a space X is a continuous map f from the closed unit interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[0, 1] into X. The point f(0) is the initial point of f; the point f(1) is the terminal point of f.
Path-connected: A space X is path-connected if, for every two points x, y in X, there is a path f from x to y, i.e., a path with initial point f(0) = x and terminal point f(1) = y. Every path-connected space is connected.
Path-connected component: A path-connected component of a space is a maximal nonempty path-connected subspace. The set of path-connected components of a space is a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of that space, which is finer
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
than the partition into connected components. The set of path-connected components of a space X is denoted π0(X).
π-base: A collection B of nonempty open sets is a π-base for a topology τ if every nonempty open set in τ includes a set from B.
Point: A point is an element of a topological space. More generally, a point is an element of any set with an underlying topological structure; e.g. an element of a metric space or a topological group is also a "point".
Point of closure: See Closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
.
Polish
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
: A space is Polish if it is separable and topologically complete, i.e. if it is homeomorphic to a separable and complete metric space.
P-point: A point of a topological space is a P-point if its filter of neighbourhoods is closed under countable intersections.
Pre-compact: See Relatively compact.
Product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
: If {Xi} is a collection of spaces and X is the (set-theoretic) product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of {Xi}, then the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
on X is the coarsest topology for which all the projection maps are continuous.
Proper function/mapping: A continuous function f from a space X to a space Y is proper if f−1(C) is a compact set in X for any compact subspace C of Y.
Proximity space
Proximity space
In topology, a proximity space is an axiomatization of notions of "nearness" that hold set-to-set, as opposed to the better known point-to-set notions that characterize topological spaces....
: A proximity space (X, δ) is a set X equipped with a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
δ between subsets of X satisfying the following properties:
- For all subsets A, B and C of X,
- A δ B implies B δ A
- A δ B implies A is non-empty
- If A and B have non-empty intersection, then A δ B
- A δ (B ∪ C) iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
(A δ B or A δ C) - If, for all subsets E of X, we have (A δ E or B δ E), then we must have A δ (X − B)
Pseudocompact: A space is pseudocompact if every real-valued
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
continuous function on the space is bounded.
Pseudometric: See Pseudometric space.
Pseudometric space: A pseudometric space (M, d) is a set M equipped with a function d : M × M → R
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
satisfying all the conditions of a metric space, except possibly the identity of indiscernibles. That is, points in a pseudometric space may be "infinitely close" without being identical. The function d is a pseudometric on M. Every metric is a pseudometric.
Punctured neighbourhood/Punctured neighborhood: A punctured neighbourhood of a point x is a neighbourhood of x, minus {x}. For instance, the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
(−1, 1) = {y : −1 < y < 1} is a neighbourhood of x = 0 in the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, so the set (−1, 0) ∪ (0, 1) = (−1, 1) − {0} is a punctured neighbourhood of 0.
Q
Quasicompact: See compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. Some authors define "compact" to include the Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
separation axiom, and they use the term quasicompact to mean what we call in this glossary simply "compact" (without the Hausdorff axiom). This convention is most commonly found in French, and branches of mathematics heavily influenced by the French.
Quotient map: If X and Y are spaces, and if f is a surjection from X to Y, then f is a quotient map (or identification map) if, for every subset U of Y, U is open in Y if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
f -1(U) is open in X. In other words, Y has the f-strong topology. Equivalently,
is a quotient map if and only if it is the transfinite composition of maps , where is a subset. Note that this doesn't imply that f is an open function.Quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
: If X is a space, Y is a set, and f : X → Y is any surjective function, then the quotient topology
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
on Y induced by f is the finest topology for which f is continuous. The space X is a quotient space or identification space. By definition, f is a quotient map. The most common example of this is to consider an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on X, with Y the set of equivalence classes and f the natural projection map. This construction is dual to the construction of the subspace topology.
R
Refinement: A cover K is a refinement of a cover L if every member of K is a subset of some member of L.Regular
Regular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
: A space is regular
Regular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
if, whenever C is a closed set and x is a point not in C, then C and x have disjoint neighbourhoods.
Regular Hausdorff: A space is regular Hausdorff (or T3) if it is a regular T0 space. (A regular space is Hausdorff if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is T0, so the terminology is consistent.)
Regular open: An open subset U of a space X is regular open if it equals the interior of its closure. An example of a non-regular open set is the set U = (0, 1) U (1, 2) in R with its normal topology, since 1 is in the interior of the closure of U, but not in U. The regular open subsets of a space form a complete Boolean algebra
Complete Boolean algebra
In mathematics, a complete Boolean algebra is a Boolean algebra in which every subset has a supremum . Complete Boolean algebras are used to construct Boolean-valued models of set theory in the theory of forcing...
.
Relatively compact: A subset Y of a space X is relatively compact in X if the closure of Y in X is compact.
Residual: If X is a space and A is a subset of X, then A is residual in X if the complement of A is meagre in X. Also called comeagre or comeager.
Resolvable: A topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is called resolvable
Resolvable space
In topology, a topological space is said to be resolvable if it is expressible as the union of two disjoint dense subsets. For instance, the real numbers form a resolvable topological space because the rationals and irrationals are disjoint dense subsets...
if it is expressible as the union of two disjoint dense subsets.
Rim-compact: A space is rim-compact if it has a base of open sets whose boundaries are compact.
S
Second category: See Meagre.Second-countable
Second-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
: A space is second-countable
Second-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
if it has a countable base for its topology. Every second-countable space is first-countable, separable, and Lindelöf.
Semilocally simply connected: A space X is semilocally simply connected if, for every point x in X, there is a neighbourhood U of x such that every loop at x in U is homotopic in X to the constant loop x. Every simply connected space and every locally simply connected space is semilocally simply connected. (Compare with locally simply connected; here, the homotopy is allowed to live in X, whereas in the definition of locally simply connected, the homotopy must live in U.)
Semiregular
Semiregular space
A semiregular space is a topological space whose regular open sets form a base.Every regular space is semiregular, and every topological space may be embedded into a semiregular space....
: A space is semiregular if the regular open sets form a base.
Separable: A space is separable if it has a countable dense subset.
Separated
Separated sets
In topology and related branches of mathematics, separated sets are pairs of subsets of a given topological space that are related to each other in a certain way....
: Two sets A and B are separated
Separated sets
In topology and related branches of mathematics, separated sets are pairs of subsets of a given topological space that are related to each other in a certain way....
if each is disjoint from the other's closure.
Sequentially compact: A space is sequentially compact if every sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
has a convergent subsequence. Every sequentially compact space is countably compact, and every first-countable, countably compact space is sequentially compact.
Short map
Short map
In the mathematical theory of metric spaces, a metric map is a function between metric spaces that does not increase any distance .These maps are the morphisms in the category of metric spaces, Met ....
: See metric map
Simply connected
Simply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
: A space is simply connected
Simply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
if it is path-connected and every loop is homotopic to a constant map.
Smaller topology: See Coarser topology.
Star: The star of a point in a given cover
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is the union of all the sets in the cover that contain the point. See star refinement
Star refinement
In mathematics, specifically in the study of topology and open covers of a topological space X, a star refinement is a particular kind of refinement of an open cover of X....
.
-Strong topology: Let be a map of topological spaces. We say that has the -strong topology if, for every subset , one has that is open in if and only if is open in Stronger topology: See Finer topology. Beware, some authors, especially analyst
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
s, use the term weaker topology.
Subbase
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
: A collection of open sets is a subbase
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
(or subbasis) for a topology if every non-empty proper open set in the topology is a union of finite intersections of sets in the subbase. If B is any collection of subsets of a set X, the topology on X generated by B is the smallest topology containing B; this topology consists of the empty set, X and all unions of finite intersections of elements of B.
Subbasis
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
: See Subbase
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
.
Subcover: A cover K is a subcover (or subcovering) of a cover L if every member of K is a member of L.
Subcovering: See Subcover.
Submaximal space: A topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is said to be submaximal if every subset of it is locally closed, that is, every subset is the intersection of an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and a closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
.
Here are some facts about submaximality as a property of topological spaces:
- Every door spaceDoor spaceIn mathematics, in the field of topology, a topological space is said to be a door space if every subset is either open or closed. The term comes from the introductory topology mnemonic that "a subset is not like a door: it can be open, closed, both, or neither".Here are some easy facts about door...
is submaximal. - Every submaximal space is weakly submaximal viz every finite set is locally closed.
- Every submaximal space is irresolvable
Subspace: If T is a topology on a space X, and if A is a subset of X, then the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
on A induced by T consists of all intersections of open sets in T with A. This construction is dual to the construction of the quotient topology.
T
T0: A space is T0 (or Kolmogorov) if for every pair of distinct points x and y in the space, either there is an open set containing x but not y, or there is an open set containing y but not x.T1
T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
: A space is T1
T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
(or Fréchet or accessible) if for every pair of distinct points x and y in the space, there is an open set containing x but not y. (Compare with T0; here, we are allowed to specify which point will be contained in the open set.) Equivalently, a space is T1 if all its singletons are closed. Every T1 space is T0.
T2: See Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
T3: See Regular Hausdorff.
T3½
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
: See Tychonoff space
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
.
T4: See Normal Hausdorff.
T5: See Completely normal Hausdorff.
Top
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
: See Category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
.
Topological invariant: A topological invariant is a property which is preserved under homeomorphism. For example, compactness and connectedness are topological properties, whereas boundedness and completeness are not. Algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
is the study of topologically invariant abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
constructions on topological spaces.
Topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
: A topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
(X, T) is a set X equipped with a collection T of subsets of X satisfying the following axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s:
-
- The empty set and X are in T.
- The union of any collection of sets in T is also in T.
- The intersection of any pair of sets in T is also in T.
- The collection T is a topology on X.
Topological sum: See Coproduct topology.
Topologically complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
: A space is topologically complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
if it is homeomorphic to a complete metric space.
Topology: See Topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
.
Totally bounded: A metric space M is totally bounded if, for every r > 0, there exist a finite cover of M by open balls of radius r. A metric space is compact if and only if it is complete and totally bounded.
Totally disconnected: A space is totally disconnected if it has no connected subset with more than one point.
Trivial topology
Trivial topology
In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
: The trivial topology
Trivial topology
In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
(or indiscrete topology) on a set X consists of precisely the empty set and the entire space X.
Tychonoff
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
: A Tychonoff space
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
(or completely regular Hausdorff space, completely T3 space, T3.5 space) is a completely regular T0 space. (A completely regular space is Hausdorff if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is T0, so the terminology is consistent.) Every Tychonoff space is regular Hausdorff.
U
Ultra-connected: A space is ultra-connected if no two non-empty closed sets are disjoint. Every ultra-connected space is path-connected.Ultrametric: A metric is an ultrametric if it satisfies the following stronger version of the triangle inequality: for all x, y, z in M, d(x, z) ≤ max(d(x, y), d(y, z)).
Uniform isomorphism
Uniform isomorphism
In the mathematical field of topology a uniform isomorphism or uniform homeomorphism is a special isomorphism between uniform spaces which respects uniform properties.-Definition:...
: If X and Y are uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s, a uniform isomorphism from X to Y is a bijective function f : X → Y such that f and f−1 are uniformly continuous. The spaces are then said to be uniformly isomorphic and share the same uniform properties.
Uniformizable/Uniformisable: A space is uniformizable if it is homeomorphic to a uniform space.
Uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
: A uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
is a set U equipped with a nonempty collection Φ of subsets of the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
X × X satisfying the following axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s:
-
- if U is in Φ, then U contains { (x, x) | x in X }.
- if U is in Φ, then { (y, x) | (x, y) in U } is also in Φ
- if U is in Φ and V is a subset of X × X which contains U, then V is in Φ
- if U and V are in Φ, then U ∩ V is in Φ
- if U is in Φ, then there exists V in Φ such that, whenever (x, y) and (y, z) are in V, then (x, z) is in U.
- The elements of Φ are called entourages, and Φ itself is called a uniform structure on U.
Uniform structure: See Uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
.
W
Weak topologyWeak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
: The weak topology
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
on a set, with respect to a collection of functions from that set into topological spaces, is the coarsest topology on the set which makes all the functions continuous.
Weaker topology: See Coarser topology. Beware, some authors, especially analyst
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
s, use the term stronger topology.
Weakly countably compact: A space is weakly countably compact (or limit point compact) if every infinite subset has a limit point.
Weakly hereditary: A property of spaces is said to be weakly hereditary if whenever a space has that property, then so does every closed subspace of it. For example, compactness and the Lindelöf property are both weakly hereditary properties, although neither is hereditary.
Weight: The weight of a space X is the smallest cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
κ such that X has a base of cardinal κ. (Note that such a cardinal number exists, because the entire topology forms a base, and because the class of cardinal numbers is well-ordered.)
Well-connected: See Ultra-connected. (Some authors use this term strictly for ultra-connected compact spaces.)