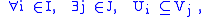Star refinement
Encyclopedia
In mathematics
, specifically in the study of topology
and open covers of a topological space
X, a star refinement is a particular kind of refinement of an open cover of X.
Given x in X and an open cover {Ui} of X with index set
I, the star of x with respect to the cover is the set of i in I such that x is in Ui. That is,
For each x we can take the union
of the sets in its star; this is also called the star of x. That is,
Then this open cover is a star refinement of some other open cover {Vj}, with index set J, if
That is,
Actually, the star condition alone is enough; the refinement condition follows (except in a degenerate case when X is the empty set
).
Star refinements are used in the definition of fully normal space and in one definition of uniform space
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in the study of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and open covers of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X, a star refinement is a particular kind of refinement of an open cover of X.
Given x in X and an open cover {Ui} of X with index set
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
I, the star of x with respect to the cover is the set of i in I such that x is in Ui. That is,
For each x we can take the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of the sets in its star; this is also called the star of x. That is,
Then this open cover is a star refinement of some other open cover {Vj}, with index set J, if
- each Ui is contained in some Vj (the refinement condition), and
- each star U*(x) is contained in a Vj (star condition).
That is,
Actually, the star condition alone is enough; the refinement condition follows (except in a degenerate case when X is the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
).
Star refinements are used in the definition of fully normal space and in one definition of uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
.