
Countable chain condition
Encyclopedia
In order theory
, a partially ordered set
X is said to satisfy the countable chain condition, or to be ccc, if every strong antichain in X is countable. There are really two conditions: the upwards and downwards countable chain conditions. These are not equivalent. We adopt the convention the countable chain condition means the downwards countable chain condition, in other words no two elements have a common lower bound.
This is called the "countable chain condition" rather than the more logical term "countable antichain condition" for historical reasons related to complete Boolean algebras. (If κ is a cardinal, then in a complete Boolean algebra every antichain has size less than κ if and only if there is no descending κ-sequence of elements, so chain conditions are equivalent to antichain conditions.)
A topological space
is said to satisfy the countable chain condition if the partially ordered set of non-empty open subsets of X satisfies the countable chain condition, i.e. if every pairwise disjoint collection of non-empty open subsets of X is countable.
Every separable topological space is ccc. Every metric space
which is ccc is also separable, but in general a ccc topological space need not be separable.
For example,
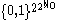
with the product topology
is ccc but not separable.
Partial orders and spaces satisfying the ccc are used in the statement of Martin's Axiom
.
In the theory of forcing, ccc partial orders are used because forcing with any generic set over such an order preserves cardinals and cofinalities.
More generally, if κ is a cardinal then a poset is said to satisfy the κ-chain condition if every antichain has size less than κ. The countable chain condition is the ℵ1-chain condition.
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
X is said to satisfy the countable chain condition, or to be ccc, if every strong antichain in X is countable. There are really two conditions: the upwards and downwards countable chain conditions. These are not equivalent. We adopt the convention the countable chain condition means the downwards countable chain condition, in other words no two elements have a common lower bound.
This is called the "countable chain condition" rather than the more logical term "countable antichain condition" for historical reasons related to complete Boolean algebras. (If κ is a cardinal, then in a complete Boolean algebra every antichain has size less than κ if and only if there is no descending κ-sequence of elements, so chain conditions are equivalent to antichain conditions.)
A topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is said to satisfy the countable chain condition if the partially ordered set of non-empty open subsets of X satisfies the countable chain condition, i.e. if every pairwise disjoint collection of non-empty open subsets of X is countable.
Every separable topological space is ccc. Every metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
which is ccc is also separable, but in general a ccc topological space need not be separable.
For example,
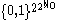
with the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
is ccc but not separable.
Partial orders and spaces satisfying the ccc are used in the statement of Martin's Axiom
Martin's axiom
In the mathematical field of set theory, Martin's axiom, introduced by , is a statement which is independent of the usual axioms of ZFC set theory. It is implied by the continuum hypothesis, so certainly consistent with ZFC, but is also known to be consistent with ZF + ¬ CH...
.
In the theory of forcing, ccc partial orders are used because forcing with any generic set over such an order preserves cardinals and cofinalities.
More generally, if κ is a cardinal then a poset is said to satisfy the κ-chain condition if every antichain has size less than κ. The countable chain condition is the ℵ1-chain condition.

