
Strong antichain
Encyclopedia
In order theory
, a subset
A of a partially ordered set
X is said to be a strong downwards antichain if no two elements have a common lower bound, that is,
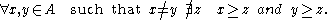
A strong upwards antichain is defined similarly.
A strong antichain is an antichain
.
Often authors will drop the upwards/downwards term and merely refer to strong antichains. Unfortunately, there is no common convention as to which version is called a strong antichain.
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
A of a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
X is said to be a strong downwards antichain if no two elements have a common lower bound, that is,
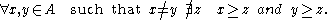
A strong upwards antichain is defined similarly.
A strong antichain is an antichain
Antichain
In mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...
.
Often authors will drop the upwards/downwards term and merely refer to strong antichains. Unfortunately, there is no common convention as to which version is called a strong antichain.

