
Antichain
Encyclopedia
In mathematics
, in the area of order theory
, an antichain is a subset of a partially ordered set
such that any two elements in the subset are incomparable. (Some authors use the term "antichain" to mean strong antichain, a subset such that there is no element of the poset
smaller than 2 distinct elements of the antichain.)
Let S be a partially ordered set. We say two elements a and b of a partially ordered set are comparable
if a ≤ b or b ≤ a. If two elements are not comparable, we say they are incomparable; that is, x and y are incomparable if neither x ≤ y nor y ≤ x.
A chain in S is a subset
C of S in which each pair of elements is comparable; that is, C is totally ordered
. An antichain in S is a subset
A of S in which each pair of different elements is incomparable; that is, there is no order relation between any two different elements in A.
states that this bound can always be reached: there always exists an antichain, and a partition of the elements into chains, such that the number of chains equals the number of elements in the antichain, which must therefore also equal the width. Similarly, we can define the height of a partial order to be the maximum cardinality of a chain. A dual of Dilworth's theorem states similarly that in any partial order of finite height, the height equals the smallest number of antichains into which the order may be partitioned.
. The number of different Sperner families is counted by the Dedekind number
s, the first few of which numbers are
Even the empty set has two antichains in its power set: one containing a single set (the empty set itself) and one containing no sets.
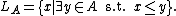
In a finite partial order (or more generally a partial order satisfying the ascending chain condition
) all lower sets have this form. The union of any two lower sets is another lower set, and the union operation corresponds in this way to a join operation
on antichains: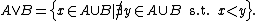
Similarly, we can define a meet operation on antichains, corresponding to the intersection of lower sets:
The join and meet operations on all finite antichains of finite subsets of a set X define a distributive lattice
, the free distributive lattice generated by X. Birkhoff's representation theorem
for distributive lattices states that every finite distributive lattice can be represented via join and meet operations on antichains of a finite partial order, or equivalently as union and intersection operations on the lower sets of the partial order.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the area of order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, an antichain is a subset of a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
such that any two elements in the subset are incomparable. (Some authors use the term "antichain" to mean strong antichain, a subset such that there is no element of the poset
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
smaller than 2 distinct elements of the antichain.)
Let S be a partially ordered set. We say two elements a and b of a partially ordered set are comparable
Comparability
In mathematics, any two elements x and y of a set P that is partially ordered by a binary relation ≤ are comparable when either x ≤ y or y ≤ x...
if a ≤ b or b ≤ a. If two elements are not comparable, we say they are incomparable; that is, x and y are incomparable if neither x ≤ y nor y ≤ x.
A chain in S is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
C of S in which each pair of elements is comparable; that is, C is totally ordered
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
. An antichain in S is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
A of S in which each pair of different elements is incomparable; that is, there is no order relation between any two different elements in A.
Height and width
A maximal antichain is an antichain that is not a proper subset of any other antichain. A maximum antichain is an antichain that has cardinality at least as large as every other antichain. The width of a partially ordered set is the cardinality of a maximum antichain. Any antichain can intersect any chain in at most one element, so, if we can partition the elements of an order into k chains then the width of the order must be at most k. Dilworth's theoremDilworth's theorem
In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains...
states that this bound can always be reached: there always exists an antichain, and a partition of the elements into chains, such that the number of chains equals the number of elements in the antichain, which must therefore also equal the width. Similarly, we can define the height of a partial order to be the maximum cardinality of a chain. A dual of Dilworth's theorem states similarly that in any partial order of finite height, the height equals the smallest number of antichains into which the order may be partitioned.
Sperner families
An antichain in the inclusion ordering of subsets of an n-element set is known as a Sperner familySperner family
In combinatorics, a Sperner family , named in honor of Emanuel Sperner, is a set system in which no element is contained in another. Formally,...
. The number of different Sperner families is counted by the Dedekind number
Dedekind number
Image:Monotone Boolean functions 0,1,2,3.svg|400px|thumb|right| The free distributive lattices of monotonic Boolean functions on 0, 1, 2, and 3 arguments, with 2, 3, 6, and 20 elements respectively...
s, the first few of which numbers are
- 2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788 .
Even the empty set has two antichains in its power set: one containing a single set (the empty set itself) and one containing no sets.
Join and meet operations
Any antichain A corresponds to a lower set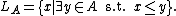
In a finite partial order (or more generally a partial order satisfying the ascending chain condition
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
) all lower sets have this form. The union of any two lower sets is another lower set, and the union operation corresponds in this way to a join operation
on antichains:
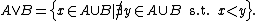
Similarly, we can define a meet operation on antichains, corresponding to the intersection of lower sets:

The join and meet operations on all finite antichains of finite subsets of a set X define a distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
, the free distributive lattice generated by X. Birkhoff's representation theorem
Birkhoff's representation theorem
In mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets...
for distributive lattices states that every finite distributive lattice can be represented via join and meet operations on antichains of a finite partial order, or equivalently as union and intersection operations on the lower sets of the partial order.

