Image:Monotone Boolean functions 0,1,2,3.svg|400px|thumb|right| The free distributive lattices of monotonic Boolean functions on 0, 1, 2, and 3 arguments, with 2, 3, 6, and 20 elements respectively (move mouse over right diagram to see description)

circle 659 623 30
circle 658 552 35
circle 587 480 35
circle 659 481 35
circle 729 481 35
circle 588 410 35
circle 658 410 35
circle 729 410 35
circle 548 339 30
circle 604 339 30
circle 758 339 30
circle 661 339 35
circle 588 268 35
circle 659 267 35
circle 729 268 35
circle 588 197 35
circle 658 197 35
circle 729 197 35
circle 658 126 35
circle 659 56 30

desc bottom-left


In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Dedekind numbers are a rapidly-growing sequence of integers

Integer sequence

In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...

 named after Richard Dedekind

Richard Dedekind

Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...

, who defined them in 1897. The Dedekind number M(n) counts the number of monotonic Boolean functions of n variables. Equivalently, it counts the number of antichains of subsets of an n-element set, the number of elements in a free distributive lattice with n generators, or the number of abstract simplicial complex

Abstract simplicial complex

In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...

es with n elements.

Accurate asymptotic

Asymptotic expansion

In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...

 estimates of M(n) and an exact expression as a summation

Summation

Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...

, are known. However Dedekind's problem of computing the values of M(n) remains difficult: no closed-form expression for M(n) is known, and exact values of M(n) have been found only for n ≤ 8.

Definitions

A Boolean function is a function that takes as input n Boolean variables (that is, values that can be either false or true, or equivalently binary values

Bit

A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...

 that can be either 0 or 1), and produces as output another Boolean variable. It is monotonic if, for every combination of inputs, switching one of the inputs from false to true can only cause the output to switch from false to true and not from true to false. The Dedekind number M(n) is the number of different monotonic Boolean functions on n variables.

An antichain

Antichain

In mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...

 of sets (also known as a Sperner family

Sperner family

In combinatorics, a Sperner family , named in honor of Emanuel Sperner, is a set system in which no element is contained in another. Formally,...

) is a family of sets, none of which is contained in any other set. If V is a set of n Boolean variables, an antichain A of subsets of V defines a monotone Boolean function f, where the value of f is true for a given set of inputs if some subset of the true inputs to f belongs to A and false otherwise. Conversely every monotone Boolean function defines in this way an antichain, of the minimal subsets of Boolean variables that can force the function value to be true. Therefore, the Dedekind number M(n) equals the number of different antichains of subsets of an n-element set.

A third, equivalent way of describing the same class of objects uses lattice theory. From any two monotone Boolean functions f and g we can find two other monotone Boolean functions f ∧ g and f ∨ g, their logical conjunction

Logical conjunction

In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....

 and logical disjunction

Logical disjunction

In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...

 respectively. The family of all monotone Boolean functions on n inputs, together with these two operations, forms a distributive lattice

Distributive lattice

In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...

, the lattice given by Birkhoff's representation theorem

Birkhoff's representation theorem

In mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets...

 from the partially ordered set

Partially ordered set

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...

 of subsets of the n variables with set inclusion as the partial order. This construction produces the free distributive lattice with n generators. Thus, the Dedekind numbers count the number of elements in free distributive lattices.

The Dedekind numbers also count the number of abstract simplicial complex

Abstract simplicial complex

In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...

es on n elements, families of sets with the property that any subset of a set in the family also belongs to the family. Any antichain determines a simplicial complex, the family of subsets of antichain members, and conversely the maximal simplices in a complex form an antichain.

Example

For n = 2, there are six monotonic Boolean functions and six antichains of subsets of the two-element set {x,y}:

• The function f(x,y) = false that ignores its input values and always returns false corresponds to the empty antichain
  Empty set
  In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
  
   Ø.
• The logical conjunction
  Logical conjunction
  In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
  
   f(x,y) = x ∧ y corresponds to the antichain { {x,y} } containing the single set {x,y}.
• The function f(x,y) = x that ignores its second argument and returns the first argument corresponds to the antichain { {x} } containing the single set {x}
• The function f(x,y) = y that ignores its first argument and returns the second argument corresponds to the antichain { {y} } containing the single set {y}
• The logical disjunction
  Logical disjunction
  In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
  
   f(x,y) = x ∨ y corresponds to the antichain { {x}, {y} } containing the two sets {x} and {y}.
• The function f(x,y) = true that ignores its input values and always returns true corresponds to the antichain {Ø} containing only the empty set.

Values

The exact values of the Dedekind numbers are known for 0 ≤ n ≤ 8:

2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788 .

The first six of these numbers are given by . M(6) was calculated by , M(7) was calculated by and , and M(8) by .

If n is even, then M(n) must also be even.
The calculation of the fifth Dedekind number M(5) = 7581 disproved a conjecture by Garrett Birkhoff

Garrett Birkhoff

Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....

 that M(n) is always divisible by (2n − 1)(2n − 2).

Summation formula

proved the following formula for the Dedekind numbers:
where
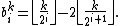
However, this formula is not helpful for computing the values of M(n) for large n due to the large number of terms in the summation.

Asymptotics

The logarithm

Logarithm

The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...

of the Dedekind numbers can be estimated accurately via the bounds
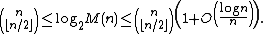
Here the left inequality counts the number of antichains in which each set has exactly 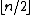elements, and the right inequality was proven by .

provided the even more accurate estimates
for even n, and
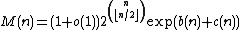
for odd n, where
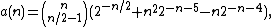
and
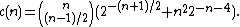
The main idea behind these estimates is that, in most antichains, all the sets have sizes that are very close to n/2. For n = 2, 4, 6, 8 Korshunov's formula provides an estimate that is inaccurate by a factor of 9.8%, 10.2%, 4.1%, and -3.3%, respectively.