
Reflective subcategory
Encyclopedia
In mathematics
, a subcategory
A of a category
B is said to be reflective in B when the inclusion functor from A to B has a left adjoint. This adjoint is sometimes called a reflector. Dually, A is said to be coreflective in B when the inclusion functor has a right adjoint.
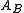 and a B-morphism
and a B-morphism
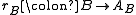 such that for each B-morphism
such that for each B-morphism 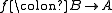 there exists a unique A-morphism
there exists a unique A-morphism 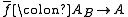 with
with 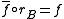 .
.
The pair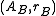 is called the A-reflection of B. The morphism
is called the A-reflection of B. The morphism 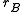 is called A-reflection arrow. (Although often, for the sake of brevity, we speak about
is called A-reflection arrow. (Although often, for the sake of brevity, we speak about 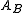 only as about the A-reflection of B.
only as about the A-reflection of B.
This is equivalent to saying that the embedding functor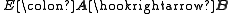 is adjoint. The coadjoint functor
is adjoint. The coadjoint functor 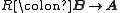 is called the reflector. The map
is called the reflector. The map  is the unit of this adjunction.
is the unit of this adjunction.
The reflector assigns to the A-object
the A-object 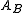 and
and 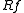 for a B-morphism
for a B-morphism 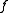 is determined by
is determined by
the commuting diagram
If all A-reflection arrows are (extremal) epimorphism
s, then the subcategory A is said to be (extremal) epireflective. Similarly, it is bireflective if all reflection arrows are bimorphisms.
All these notions are special case of the common generalization —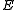 -reflective subcategory, where
-reflective subcategory, where 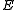 is a class of morphisms.
is a class of morphisms.
The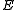 -reflective hull of a class A of objects is defined as the smallest
-reflective hull of a class A of objects is defined as the smallest 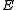 -reflective subcategory containing A. Thus we can speak about reflective hull, epireflective hull, extremal epireflective hull, etc.
-reflective subcategory containing A. Thus we can speak about reflective hull, epireflective hull, extremal epireflective hull, etc.
Dual
notions to the above mentioned notions are coreflection, coreflection arrow, (mono)coreflective subcategory, coreflective hull.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a subcategory
Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
A of a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
B is said to be reflective in B when the inclusion functor from A to B has a left adjoint. This adjoint is sometimes called a reflector. Dually, A is said to be coreflective in B when the inclusion functor has a right adjoint.
Definition
A subcategory A of a category B is said to be reflective in B if for each B-object B there exists an A-object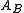 and a B-morphism
and a B-morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
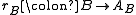 such that for each B-morphism
such that for each B-morphism 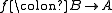 there exists a unique A-morphism
there exists a unique A-morphism 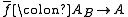 with
with 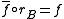 .
.The pair
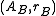 is called the A-reflection of B. The morphism
is called the A-reflection of B. The morphism 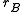 is called A-reflection arrow. (Although often, for the sake of brevity, we speak about
is called A-reflection arrow. (Although often, for the sake of brevity, we speak about 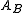 only as about the A-reflection of B.
only as about the A-reflection of B.This is equivalent to saying that the embedding functor
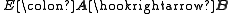 is adjoint. The coadjoint functor
is adjoint. The coadjoint functor 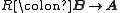 is called the reflector. The map
is called the reflector. The map 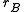 is the unit of this adjunction.
is the unit of this adjunction.The reflector assigns to
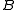 the A-object
the A-object 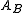 and
and 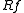 for a B-morphism
for a B-morphism 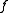 is determined by
is determined bythe commuting diagram
If all A-reflection arrows are (extremal) epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s, then the subcategory A is said to be (extremal) epireflective. Similarly, it is bireflective if all reflection arrows are bimorphisms.
All these notions are special case of the common generalization —
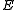 -reflective subcategory, where
-reflective subcategory, where 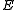 is a class of morphisms.
is a class of morphisms.The
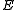 -reflective hull of a class A of objects is defined as the smallest
-reflective hull of a class A of objects is defined as the smallest 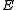 -reflective subcategory containing A. Thus we can speak about reflective hull, epireflective hull, extremal epireflective hull, etc.
-reflective subcategory containing A. Thus we can speak about reflective hull, epireflective hull, extremal epireflective hull, etc.Dual
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
notions to the above mentioned notions are coreflection, coreflection arrow, (mono)coreflective subcategory, coreflective hull.
Algebra
- The category of abelian groupsCategory of abelian groupsIn mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
Ab is a reflective subcategory of the category of groupsCategory of groupsIn mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, Grp. The reflector is the functor which sends each group to its abelianization. In its turn, the category of groupsCategory of groupsIn mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
is a reflective subcategory of the category of inverse semigroupInverse semigroupIn mathematics, an inverse semigroup S is a semigroup in which every element x in S has a unique inversey in S in the sense that x = xyx and y = yxy...
s. - Similarly, the category of commutative associative algebras is a reflective subcategory of all associative algebras, where the reflector is quotienting out by the commutator ideal. This is used in the construction of the symmetric algebraSymmetric algebraIn mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
from the tensor algebraTensor algebraIn mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
. - Dually, the category of anti-commutative associative algebras is a reflective subcategory of all associative algebras, where the reflector is quotienting out by the anti-commutator ideal. This is used in the construction of the exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
from the tensor algebraTensor algebraIn mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
. - The category of fieldsField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is a reflective subcategory of the category of integral domains. The reflector is the functor which sends each integral domain to its field of fractionsField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
. - The category of abelian torsion groups is a coreflective subcategory of the category of abelian groupsCategory of abelian groupsIn mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
. The coreflector is the functor sending each group to its torsion subgroupTorsion subgroupIn the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
. - The categories of elementary abelian groupElementary Abelian groupIn group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
s, abelian p-groups, and p-groups are all reflective subcategories of the category of groups, and the kernels of the reflection maps are important objects of study; see focal subgroup theoremFocal subgroup theoremIn abstract algebra, the focal subgroup theorem describes the fusion of elements in a Sylow subgroup of a finite group. The focal subgroup theorem was introduced in and is the "first major application of the transfer" according to . The focal subgroup theorem relates the ideas of transfer and...
. - The category of vector spacesCategory of vector spacesIn mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
over the field k is a (non full) reflective subcategory of the category of sets. The reflector is the functor which sends each set B in the free vector space generated by B over k, that can be identified with the vector space of all k valued functions on B vanishing outside a finite set. In similar way, several free construction functors are reflectors of the category of sets onto the corresponding reflective subcategory.
Topology
- Kolmogorov spaceKolmogorov spaceIn topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
s (T0 spaces) are a reflective subcategory of Top, the category of topological spacesCategory of topological spacesIn mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
, and the Kolmogorov quotient is the reflector. - The category of completely regular spaces CReg is a reflective subcategory of Top. By taking Kolmogorov quotients, one sees that the subcategory of Tychonoff spaces is also reflective.
- The category of all compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s is a reflective subcategory of the category of all Tychonoff spaceTychonoff spaceIn topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
s. The reflector is given by the Stone–Čech compactificationStone–Cech compactificationIn the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
. - The category of all complete metric spaces with uniformly continuous mappings is a reflective and full subcategory of the category of metric spaces. The reflector is the completion of a metric space on objects, and the extension by density on arrows.
Functional analysis
- The category of Banach spaces is a reflective and full subcategory of the category of normed spaces and bounded linear operators. The reflector is the norm completion functor.
Category theory
- For any Grothendieck site (C,J), the toposToposIn mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
of sheavesSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on (C,J) is a reflective subcategory of the topos of presheaves on C, with the special further property that the reflector functor is left exact. The reflector is the sheafification functor a: Presh(C) → Sh(C,J), and the adjoint pair (a,i) is an important example of a geometric morphism in topos theory.

