Coherent topology
Encyclopedia
In topology
, a coherent topology is one that is uniquely determined by a family of subspaces. Loosely speaking, a topological space is coherent with a family of subspaces if it is a topological union of those subspaces.
and let C = {Cα : α ∈ A} be a family
of subspaces of X (typically C will be a cover
of X). Then X is said to be coherent with C (or determined by C) if X has the final topology
coinduced by the inclusion map
s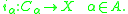
By definition, this is the finest topology on X for which the inclusion maps are continuous.
Equivalently, X is coherent with C if either of the following conditions holds:
Given a topological space X and any family of subspaces C there is unique topology on X which is coherent with C. This topology will, in general, be finer than the given topology on X.
agree on each intersection
Xα ∩ Xβ. Assume further that Xα ∩ Xβ is closed in Xα for each α,β. Then the topological union of {Xα} is the set-theoretic union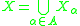
together with the final topology coinduced by the inclusion maps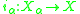
. The inclusion maps will then be topological embeddings and X will be coherent with the subspaces {Xα}.
Conversely, if X is coherent with a family of subspaces {Cα} that cover X, then X is homeomorphic to the topological union of the family {Cα}.
One can form the topological union of an arbitrary family of topological spaces as above, but if the topologies do not agree on the intersections then the inclusions will not necessarily be embeddings.
One can also describe the topological union by means of the disjoint union
. Specifically, if X is a topological union of the family {Xα}, then X is homeomorphic to the quotient
of the disjoint union of the family {Xα} by the equivalence relation
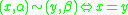
for all α, β in A. That is,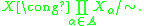
If the spaces {Xα} are all disjoint then the topological union is just the disjoint union.
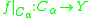
are continuous for each α ∈ A. This universal property
characterizes coherent topologies in the sense that a space X is coherent with C if and only if this property holds for all spaces Y and all functions f : X → Y.
Let X be determined by a cover
C = {Cα}. Then
Let X be determined by {Cα} and let Y be an open or closed subspace of X. Then Y is determined by {Y ∩ Cα}.
Let X be determined by {Cα} and let f : X → Y be a quotient map. Then Y is determined by {f(Cα)}.
Let f : X → Y be a surjective map and suppose Y is determined by {Dα : α ∈ A}. For each α ∈ A let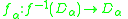
be the restriction of f to f−1(Dα). Then
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a coherent topology is one that is uniquely determined by a family of subspaces. Loosely speaking, a topological space is coherent with a family of subspaces if it is a topological union of those subspaces.
Definition
Let X be a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and let C = {Cα : α ∈ A} be a family
Indexed family
In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
of subspaces of X (typically C will be a cover
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
of X). Then X is said to be coherent with C (or determined by C) if X has the final topology
Final topology
In general topology and related areas of mathematics, the final topology on a set X, with respect to a family of functions into X, is the finest topology on X which makes those functions continuous.- Definition :Given a set X and a family of topological spaces Y_i with functionsf_i: Y_i \to Xthe...
coinduced by the inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
s
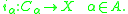
By definition, this is the finest topology on X for which the inclusion maps are continuous.
Equivalently, X is coherent with C if either of the following conditions holds:
- A subset U is openOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in X if and only if U ∩ Cα is open in Cα for each α ∈ A. - A subset U is closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
in X if and only if U ∩ Cα is closed in Cα for each α ∈ A.
Given a topological space X and any family of subspaces C there is unique topology on X which is coherent with C. This topology will, in general, be finer than the given topology on X.
Examples
- A topological space X is coherent with every open cover of X.
- A topological space X is coherent with every locally finiteLocally finite collectionIn the mathematical field of topology, local finiteness is a property of collections of subsets of a topological space. It is fundamental in the study of paracompactness and topological dimension....
closed cover of X. - A discrete spaceDiscrete spaceIn topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
is coherent with every family of subspaces (including the empty familyEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
). - A topological space X is coherent with a partition of X if and only X is homeomorphic to the disjoint unionDisjoint union (topology)In general topology and related areas of mathematics, the disjoint union of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology...
of the elements of the partition. - Finitely generated spaces are those determined by the family of all finite subspacesFinite topological spaceIn mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
. - Compactly generated spaceCompactly generated spaceIn topology, a compactly generated space is a topological space whose topology is coherent with the family of all compact subspaces. Specifically, a topological space X is compactly generated if it satisfies the following condition:Equivalently, one can replace closed with open in this definition...
s are those determined by the family of all compact subspaceCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
s. - A CW complexCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
X is coherent with its family of n-skeletons Xn.
Topological union
Let {Xα} be a family of (not necessarily disjoint) topological spaces such that the induced topologiesInduced topology
In topology and related areas of mathematics, an induced topology on a topological space is a topology which is "optimal" for some function from/to this topological space.- Definition :Let X_0, X_1 be sets, f:X_0\to X_1....
agree on each intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
Xα ∩ Xβ. Assume further that Xα ∩ Xβ is closed in Xα for each α,β. Then the topological union of {Xα} is the set-theoretic union
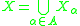
together with the final topology coinduced by the inclusion maps
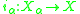. The inclusion maps will then be topological embeddings and X will be coherent with the subspaces {Xα}.Conversely, if X is coherent with a family of subspaces {Cα} that cover X, then X is homeomorphic to the topological union of the family {Cα}.
One can form the topological union of an arbitrary family of topological spaces as above, but if the topologies do not agree on the intersections then the inclusions will not necessarily be embeddings.
One can also describe the topological union by means of the disjoint union
Disjoint union (topology)
In general topology and related areas of mathematics, the disjoint union of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology...
. Specifically, if X is a topological union of the family {Xα}, then X is homeomorphic to the quotient
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of the disjoint union of the family {Xα} by the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
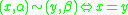
for all α, β in A. That is,
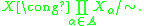
If the spaces {Xα} are all disjoint then the topological union is just the disjoint union.
Properties
Let X be coherent with a family of subspaces {Cα}. A map f : X → Y is continuous if and only if the restrictions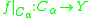are continuous for each α ∈ A. This universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
characterizes coherent topologies in the sense that a space X is coherent with C if and only if this property holds for all spaces Y and all functions f : X → Y.
Let X be determined by a cover
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
C = {Cα}. Then
- If C is a refinement of a cover D, then X is determined by D.
- If D is a refinement of C and each Cα is determined by the family of all Dβ contained in Cα then X is determined by D.
Let X be determined by {Cα} and let Y be an open or closed subspace of X. Then Y is determined by {Y ∩ Cα}.
Let X be determined by {Cα} and let f : X → Y be a quotient map. Then Y is determined by {f(Cα)}.
Let f : X → Y be a surjective map and suppose Y is determined by {Dα : α ∈ A}. For each α ∈ A let
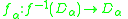
be the restriction of f to f−1(Dα). Then
- If f is continuous and each fα is a quotient map, then f is a quotient map.
- f is a closed map (resp. open map) if and only if each fα is closed (resp. open).