In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

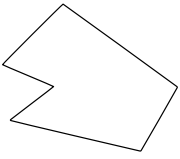
, a simple polygon is a closed polygonal chain  of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments.

A polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

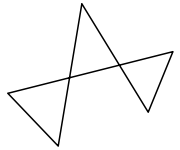
 that is not simple is called self-intersecting by geometers and complex by computer graphics

Computer graphics

Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....

 programmers (in geometry, a complex polygon

Complex polygon

The term complex polygon can mean two different things:*In computer graphics, as a polygon which is neither convex nor concave.*In geometry, as a polygon in the unitary plane, which has two complex dimensions.-Computer graphics:...

 is something different). Such a polygon does not necessarily have a well-defined inside and outside.

Simple polygons are also called Jordan polygons, because the Jordan curve theorem

Jordan curve theorem

In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...

 can be used to prove that such a polygon divides the plane into two regions, the region inside it and the region outside it. A simple polygon in the plane is topologically equivalent to a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

 and its interior is topologically equivalent to a disk

Disk (mathematics)

In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...

.

Weakly simple polygon

If a closed polygonal chain embedded in the plane divides it into two regions one of which is topologically equivalent to a disk, then the chain is called a weakly simple polygon. Informally, a weakly simple polygon is a polygon in which some sides can "touch" but cannot "cross over".

In the image on the left, ABCDEFGHJKLM is a weakly simple polygon with the color blue marking its interior.

In a more general definition of weakly simple polygons, they are the limits of sequences of simple polygons of the same combinatorial type, with the convergence under the Hausdorff metric. They not necessarily define an "interior". For example, referring to the image above, the polygonal chain ABCBA is a weakly simple polygon: it may be viewed as the limit of "squeezing" of the polygon ABCFGHA.

Non-simple weakly simple polygons arise in computer graphics and CAD as a computer representation of polygonal regions with holes: for each hole a "cut" is created to connect it to an external boundary. Referring to the image above, ABCM is an external boundary of a planar region with a hole FGHJ. The cut ED connects the hole with the exterior and is traversed twice in the resulting weakly simple polygonal representation.

Computational problems

In computational geometry

Computational geometry

Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...

, several important computational tasks involve inputs in the form of a simple polygon; in each of these problems, the distinction between the interior and exterior is crucial in the problem definition.

• Point in polygon
  Point in polygon
  In computational geometry, the point-in-polygon problem asks whether a given point in the plane lies inside, outside, or on the boundary of a polygon...
  
   testing involves determining, for a simple polygon P and a query point q, whether q lies interior to P.
• Simple formulae are known for computing polygon area; that is, the area of the interior of the polygon.
• Polygon triangulation
  Polygon triangulation
  In computational geometry, polygon triangulation is the decomposition of a polygonal area P into a set of triangles, i.e., finding the set of triangles with pairwise non-intersecting interiors whose union is P....
  
  : dividing a simple polygon into triangles. Although convex polygons are easy to triangulate, triangulating a general simple polygon is more difficult because we have to avoid adding edges that cross outside the polygon. Nevertheless, Bernard Chazelle
  Bernard Chazelle
  Bernard Chazelle is the Eugene Higgins Professor of Computer Science at Princeton University. Much of his work is in computational geometry, where he has found many of the best-known algorithms, such as linear-time triangulation of a simple polygon, as well as many useful complexity results, such...
  
   showed in 1991 that any simple polygon with n vertices can be triangulated in Θ(n) time, which is optimal. The same algorithm may also be used for determining whether a closed polygonal chain forms a simple polygon.
• Polygon union: finding the simple polygon or polygons containing the area inside either of two simple polygons
• Polygon intersection: finding the simple polygon or polygons containing the area inside both of two simple polygons
• The convex hull
  Convex hull
  In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
  
   of a simple polygon may be computed more efficiently than the complex hull of other types of inputs, such as the convex hull of a point set.
• Voronoi diagram
  Voronoi diagram
  In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
  
   of a simple polygon
• Medial axis
  Medial axis
  The medial axis of an object is the set of all points having more than one closest point on the object's boundary. Originally referred to as the topological skeleton, it was introduced by Blum as a tool for biological shape recognition....
  
  /topological skeleton
  Topological skeleton
  In shape analysis, skeleton of a shape is a thin version of that shape that is equidistant to its boundaries. The skeleton usually emphasizes geometrical and topological properties of the shape, such as its connectivity, topology, length, direction, and width...
  
  /straight skeleton
  Straight skeleton
  In geometry, a straight skeleton is a method of representing a polygon by a topological skeleton. It is similar in some ways to the medial axis but differs in that the skeleton is composed of straight line segments, while the medial axis of a polygon may involve parabolic curves.Straight skeletons...
  
   of a simple polygon
• Offset curve of a simple polygon
• Polygon resizing
• Minkowski sum for simple polygons