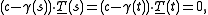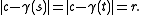Medial axis
Encyclopedia

Topological skeleton
In shape analysis, skeleton of a shape is a thin version of that shape that is equidistant to its boundaries. The skeleton usually emphasizes geometrical and topological properties of the shape, such as its connectivity, topology, length, direction, and width...
, it was introduced by Blum as a tool for biological shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
recognition.
In mathematics the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the medial axis is known as the cut locus.
In 2D, the medial axis of a plane curve S is the locus of the centers of circles that are tangent to curve S in two or more points, where all such circles are contained in S. (It follows that the medial axis itself is contained in S.)
The medial axis of a simple polygon
Simple polygon
In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
is a tree whose leaves are the vertices of the
polygon, and whose edges are either straight segments or arcs of parabolas.
The medial axis together with the associated radius function of the maximally inscribed discs is called the medial axis transform (MAT). The medial axis transform is a complete shape descriptor (see also shape analysis
Shape analysis
This article describes shape analysis to analyze and process geometric shapes.The shape analysis described here is related to the statistical analysis of geometric shapes, to shape matching and shape recognition...
), meaning that it can be used to reconstruct the shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
of the original domain.
The medial axis is a subset of the symmetry set
Symmetry set
In geometry, the symmetry set is a method for representing the local symmetries of a curve, and can be used as a method for representing the shape of objects by finding the topological skeleton...
, which is defined similarly, except that it also includes circles not contained in S. (Hence, the symmetry set of S generally extends to infinity, similar to the Voronoi diagram
Voronoi diagram
In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
of a point set.)
The medial axis generalizes to k-dimensional hypersurfaces by replacing 2D circles with k-dimension hyperspheres. The 2D medial axis is useful for character
Optical character recognition
Optical character recognition, usually abbreviated to OCR, is the mechanical or electronic translation of scanned images of handwritten, typewritten or printed text into machine-encoded text. It is widely used to convert books and documents into electronic files, to computerize a record-keeping...
and object recognition, while the 3D medial axis has applications in surface reconstruction
Surface reconstruction
Surface reconstruction refers to the process by which atoms at the surface of a crystal assume a different structure than that of the bulk. Surface reconstructions are important in that they help in the understanding of surface chemistry for various materials, especially in the case where another...
for physical models, and for dimensional reduction of complex models.
If S is given by a unit speed parametrisation
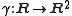 , and
, and 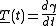 is the unit tangent vector at each point. Then there will be a bitangent circle with center c and radius r if
is the unit tangent vector at each point. Then there will be a bitangent circle with center c and radius r if
For most curves, the symmetry set will form a one dimensional curve and can contain cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
. The symmetry set has end points corresponding to the vertices
Vertex (curve)
In the geometry of curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant...
of S.
See also
- Voronoi diagramVoronoi diagramIn mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
- which can be regarded as a discrete form of the medial axis. - Cut locus
- Straight skeletonStraight skeletonIn geometry, a straight skeleton is a method of representing a polygon by a topological skeleton. It is similar in some ways to the medial axis but differs in that the skeleton is composed of straight line segments, while the medial axis of a polygon may involve parabolic curves.Straight skeletons...
- Shape analysisShape analysisThis article describes shape analysis to analyze and process geometric shapes.The shape analysis described here is related to the statistical analysis of geometric shapes, to shape matching and shape recognition...
- Local feature sizeLocal feature sizeLocal feature size refers to several related concepts in computer graphics and computational geometry for measuring the size of a geometric object near a particular point....
External links
- Variational Symmetry Axis
- The Scale Axis Transform - a generalization of the medial axis
- Straight Skeleton for polygon with holes - Straight Skeleton builder implemented in java.
- Multi-layered medial axis - a generalization of the medial axis (for e.g. representing an airport or a multi-storey building)