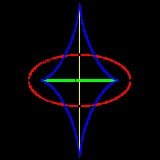
Symmetry set
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the symmetry set is a method for representing the local symmetries of a curve, and can be used as a method for representing the shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
of objects by finding the topological skeleton
Topological skeleton
In shape analysis, skeleton of a shape is a thin version of that shape that is equidistant to its boundaries. The skeleton usually emphasizes geometrical and topological properties of the shape, such as its connectivity, topology, length, direction, and width...
. The medial axis
Medial axis
The medial axis of an object is the set of all points having more than one closest point on the object's boundary. Originally referred to as the topological skeleton, it was introduced by Blum as a tool for biological shape recognition....
, a subset of the symmetry set is a set of curves which roughly run along the middle of an object.
The symmetry set in 2 dimensions
Let be an open interval, and
be an open interval, and 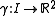 be a parametrisation of a smooth plane curve.
be a parametrisation of a smooth plane curve.The symmetry set of
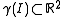 is defined to be the closure of the set of centres of circles tangent to the curve at at least distinct two points (bitangent
is defined to be the closure of the set of centres of circles tangent to the curve at at least distinct two points (bitangentBitangent
In mathematics, a bitangent to a curve C is a line L that touches C in two distinct points P and Q and that has the same direction to C at these points...
circles).
The symmetry set will have endpoints corresponding to vertices
Vertex (curve)
In the geometry of curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant...
of the curve. Such points will lie at cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
of the evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
. At such points the curve will have 4-point contact
Contact (mathematics)
In mathematics, contact of order k of functions is an equivalence relation, corresponding to having the same value at a point P and also the same derivatives there, up to order k. The equivalence classes are generally called jets...
with the circle.
The symmetry set in n dimensions
For a smooth manifold of dimension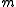 in
in 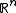 (clearly we need
(clearly we need 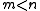 ). The symmetry set of the manifold is the closure of the centres of hyperspheres tangent to the manifold in at least two distinct places.
). The symmetry set of the manifold is the closure of the centres of hyperspheres tangent to the manifold in at least two distinct places.The symmetry set as a bifurcation set
Let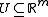 be an open simply connected domain and
be an open simply connected domain and 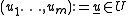 . Let
. Let 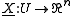 be a parametrisation of a smooth piece of manifold.
be a parametrisation of a smooth piece of manifold.We may define a
 parameter family of functions on the curve, namely
parameter family of functions on the curve, namely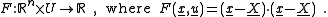
This family is called the family of distance squared functions. This is because for a fixed
 the value of
the value of 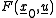 is the square of the distance from
is the square of the distance from  to
to 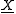 at
at 
The symmetry set is then the bifurcation set of the family of distance squared functions. I.e. it is the set of
 such that
such that 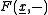 has a repeated singularity for some
has a repeated singularity for some 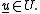
By a repeated singularity, we mean that the jacobian matrix is singular. Since we have a family of functions, this is equivalent to
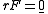 .
.The symmetry set is then the set of
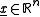 such that there exist
such that there exist 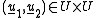 with
with 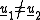 , and
, and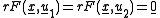
together with the limiting points of this set.

