In the geometry of curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

s, a vertex is a point of where the first derivative of curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

 is zero. This is typically a local maximum or minimum

Maxima and minima

In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...

 of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant. For a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

 which has constant curvature, every point is a vertex.

The four-vertex theorem

Four-vertex theorem

The four-vertex theorem states that the curvature function of a simple, closed, smooth plane curve has at least four local extrema...

 states that every closed curve must have at least four vertices.

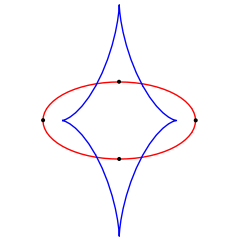
Vertices are points where the curve has 4-point contact with the osculating circle at that point. The evolute

Evolute

In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....

 of a curve will generically have a cusp

Cusp (singularity)

In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....

 when the curve has a vertex. Other, more degenerate and non-stable singularities occur at higher vertices. Higher vertices generically occur in a one-parameter family of curves when two ordinary vertices coalesce to form a higher vertex; after which they annihilate.

The symmetry set

Symmetry set

In geometry, the symmetry set is a method for representing the local symmetries of a curve, and can be used as a method for representing the shape of objects by finding the topological skeleton...

 has endpoints at the cusps corresponding to the vertices, and the medial axis

Medial axis

The medial axis of an object is the set of all points having more than one closest point on the object's boundary. Originally referred to as the topological skeleton, it was introduced by Blum as a tool for biological shape recognition....

, a subset of the symmetry set

Symmetry set

In geometry, the symmetry set is a method for representing the local symmetries of a curve, and can be used as a method for representing the shape of objects by finding the topological skeleton...

, also has its endpoints in the cusps.

If a curve is bilaterally symmetric

Reflection symmetry

Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...

, it will have a vertex at the point or points where the axis of symmetry crosses the curve. Thus, the notion of a vertex for a curve is closely related to that of an optical vertex, the point where an optical axis crosses a lens

Lens (optics)

A lens is an optical device with perfect or approximate axial symmetry which transmits and refracts light, converging or diverging the beam. A simple lens consists of a single optical element...

surface.

Vertices of a conic section

A hyperbola has two vertices, one on each branch; they are the closest of any two points lying on opposite branches of the hyperbola, and they lie on the principal axis. On a parabola, the sole vertex lies on the axis of symmetry. On an ellipse, two of the four vertices lie on the major axis and two lie on the minor axis.