The four-vertex theorem states that the curvature

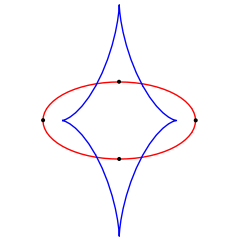
Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

 function of a simple, closed, smooth plane curve

Plane curve

In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....

  has at least four local extrema

Extrema

Extrema may refer to:*maxima and minima*Extremities*Extremophiles*Extrema, Minas Gerais, town in Brazil*Extrema, Rondônia, town in Brazil*Extrema , Italian metal band...

 (specifically, at least two local maxima and at least two local minima). The name of the theorem derives from the convention of calling an extreme point of the curvature function a vertex

Vertex (curve)

In the geometry of curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant...

.

Examples

An ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

 has exactly four vertices: two local maxima of curvature where it is crossed by the major axis of the ellipse, and two local minima of curvature where it is crossed by the minor axis. In a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

, every point is both a local maximum and a local minimum of curvature, so there are infinitely many vertices.

History

The four-vertex theorem was first proved for convex curves (i.e. curves with strictly positive curvature) in 1909 by Syamadas Mukhopadhyaya. His proof utilizes the fact that a point on the curve is an extremum of the curvature function if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

 the osculating circle

Osculating circle

In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...

 at that point has 4th-order contact

Contact (mathematics)

In mathematics, contact of order k of functions is an equivalence relation, corresponding to having the same value at a point P and also the same derivatives there, up to order k. The equivalence classes are generally called jets...

 with the curve (in general the osculating circle has only 3rd-order contact with the curve). The four-vertex theorem was proved in general by Adolf Kneser

Adolf Kneser

Adolf Kneser was a German mathematician.He was born in Grüssow, Mecklenburg, Germany and died in Breslau, Germany ....

 in 1912 using a projective argument.

Converse

The converse to the four-vertex theorem states that any continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

, real-valued function of the circle that has at least two local maxima and two local minima is the curvature function of a simple, closed plane curve. The converse was proved for strictly positive functions in 1971 by Herman Gluck as a special case of a general theorem on pre-assigning the curvature of n-spheres

Hypersphere

In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...

. The full converse to the four-vertex theorem was proved by Björn Dahlberg shortly before his death in January 1998, and published posthumously. Dahlberg's proof uses a winding number

Winding number

In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...

 argument which is in some ways reminiscent of the standard topological proof of the Fundamental Theorem of Algebra.

Application to mechanics

One corollary of the theorem is that a homogeneous, planar disk rolling
on a horizontal surface under gravity has at least 4 balance points.
There is no 3-dimensional generalization of this result, as there exists a convex, homogeneous object with exactly 2 balance points (one stable, and the other unstable): see Gömböc

Gömböc

A gömböc is a convex three-dimensional homogeneous body which, when resting on a flat surface, has just one stable and one unstable point of equilibrium. Its existence was conjectured by Russian mathematician Vladimir Arnold in 1995 and proven in 2006 by Hungarian scientists Gábor Domokos and Péter...

.

Discrete variations

There are several discrete versions of the four-vertex theorem, both for convex and non-convex polygons. Here are some of them:

• (Bilinski) The sequence of angles of a convex equilateral polygon has at least four extrema
  Maxima and minima
  In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
  
  .
• The sequence of side lengths of a convex equiangular polygon
  Equiangular polygon
  In Euclidean geometry, an equiangular polygon is a polygon whose vertex angles are equal. If the lengths of the sides are also equal then it is a regular polygon.The only equiangular triangle is the equilateral triangle...
  
   has at least four extrema
  Maxima and minima
  In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
  
  .
• (Musin) A circle
  Circle
  A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
  
   circumscribed
  Circumscribed circle
  In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
  
   around three consecutive vertices of the polygon is called extremal if it contains all remaining vertices of the polygon, or has none of them in its interior. A convex polygon is generic if it has no four vertices on the same circle. Then every generic convex polygon has at least four extremal circles.
• (Legendre
  Adrien-Marie Legendre
  Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
  
  –Cauchy
  Augustin Louis Cauchy
  Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
  
  ) Two convex n-gons with equal corresponding side length have either zero or at least 4 sign changes in the cyclic sequence of the corresponding angle differences.
• (A.D. Alexandrov
  Aleksandr Danilovich Aleksandrov
  Aleksandr Danilovich Aleksandrov , and Alexandrov ) , was a Soviet/Russian mathematician, physicist, philosopher and mountaineer.- Scientific career :...
  
  ) Two convex n-gons with parallel corresponding sides and equal area have either zero or at least 4 sign changes in the cyclic sequence of the corresponding side lengths differences.

Some of these variations are stronger than the other, and all of them imply the (usual) four-vertex theorem by a limit argument.

External links

• The Four Vertex Theorem and Its Converse -- An expository article which explains Robert Osserman
  Robert Osserman
  Robert Ossermanis an American mathematician.Raised in Bronx, he went to Bronx High School of Science and New York University.He earned a Ph.D...
  
  's simple proof of the Four-vertex theorem and Dahlberg's proof of its converse, offers a brief overview of extensions and generalizations, and gives biographical sketches of Mukhopadhyaya, Kneser and Dahlberg.