
Evolute
Encyclopedia
Differential geometry of curves
Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
, the evolute of a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
is the locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of all its centers of curvature
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
. Equivalently, it is the envelope
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of the normals
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to a curve.
The evolute of a curve, a surface, or more generally a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
, is the caustic
Caustic (mathematics)
In differential geometry and geometric optics, a caustic is the envelope of rays either reflected or refracted by a manifold. It is related to the optical concept of caustics...
of the normal map. Let M be a smooth, regular submanifold in Rn. For each point p in M and each vector v, based at p and normal to M, we associate the point . This defines a Lagrangian map, called the normal map. The caustic of the normal map is the evolute of M.
History
ApolloniusApollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
(c. 200 BC) discussed evolutes in Book V of his Conics. However, Huygens is sometimes credited with being the first to study them (1673).
Definition
Let γ(s) be a plane curve, parameterized by its arclength s. The unit tangent vector to the curve is, by virtue of the arclength parameterization,
and the unit normal to the curve is the unit vector N(s) perpendicular to T(s) chosen so that the pair (T,N) is positively oriented
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
.
The curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
k of γ is defined by means of the equation

for each s in the domain of γ. The radius of curvature
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
is the reciprocal of curvature:

The radius of curvature at γ(s) is, in magnitude, the radius of the circle which forms the best approximation of the curve to second order at the point: that is, it is the radius of the circle making second order contact
Contact (mathematics)
In mathematics, contact of order k of functions is an equivalence relation, corresponding to having the same value at a point P and also the same derivatives there, up to order k. The equivalence classes are generally called jets...
with the curve, the osculating circle
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
. The sign of the radius of curvature indicates the direction in which the osculating circle moves if it is parameterized in the same direction as the curve at the point of contact: it is positive if the circle moves in a counterclockwise sense, and negative otherwise.
The center of curvature is the center of the osculating circle. It lies on the normal line through γ(s) at a distance of R from γ(s), in the direction determined by the sign of k. In symbols, the center of curvature lies at the point:

As s varies, the center of curvature defined by this equation traces out a plane curve, the evolute of γ.
General parameterizations
If γ(t) is given a general parameterization other than the parameterization by arclength, sayγ(t) = (x(t), y(t)), then the parametric equation of the evolute can be expressed in terms of the radius of curvature R = 1/k and the tangential angle
Tangential angle
In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the x-axis. In geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent...
φ, which is the angle the tangent to the curve makes with a fixed reference axis [the x-axis]. In terms of R and φ, the evolute has the parametric equation

where the unit normal N = (−sinφ, cosφ) is obtained by rotating the unit tangent T = (cosφ, sinφ) through an angle of 90°.
The equation of the evolute may also be written entirely in terms of x, y and their derivatives. Since
 and
and 
R and φ can be eliminated to obtain for a parametrically defined function:


Properties
ArclengthSuppose that the curve γ is parameterized with respect to its arclength s. Then the arclength along the evolute E from s1 to s2 is given by

Thus, if the curvature of γ is strictly monotonic
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
, then

Equivalently, denoting the arclength parameter of the curve E by σ,

This follows by differentiation of the formula

and employing the Frenet identity N′(s) = −k(s)T(s):

whence
from which it follows that dσ/ds = |dR/ds|, as claimed.
Unit tangent vector
Another consequence of is that the tangent vector to the evolute E at E(s) is normal to the curve γ at γ(s).
Curvature
The curvature of the evolute E is obtained by differentiating E twice with respect to its arclength parameter σ. Since dσ/ds = |dR/ds|, it follows from that

where the sign is that of dR/ds. Differentiating a second time, and using the Frenet equation N′(s) = −k(s)T(s) gives

As a consequence, the curvature of E is

where R is the (signed) radius of curvature and the prime denotes the derivative with respect to s.
Relation with involute
Intrinsic equation
If φ can be expressed as a function of R, say φ = g(R), then the Whewell equation
Whewell equation
The Whewell equation of a plane curve is an equation that relates the tangential angle with arclength , where the tangential angle is angle between the tangent to the curve and the x-axis and the arc length is the distance along the curve from a fixed point...
for the evolute is Φ = g(R) + π/2, where Φ is the tangential angle of the evolute and we take R as arclength along the evolute. From this we can derive the Cesàro equation
Cesàro equation
In geometry, the Cesàro equation of a plane curve is an equation relating curvature to arc length . It may also be given as an equation relating the radius of curvature to arc length. Two congruent curves will have the same Cesàro equation...
as Κ = g′(R), where Κ is the curvature of the evolute.
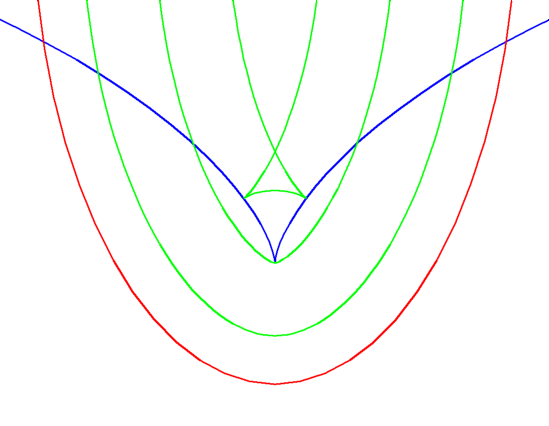
Relationship between a curve and its evolute
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
when the curve has a vertex
Vertex (curve)
In the geometry of curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant...
, that is when the curvature has a local maximum or minimum. At a point of inflection of the original curve the radius of curvature becomes infinite and so (X, Y) will become infinite, often this will result in the evolute having an asymptote
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
. Similarly, when the original curve has a cusp where the radius of curvature is 0 then the evolute will touch the original curve.
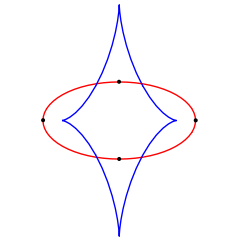
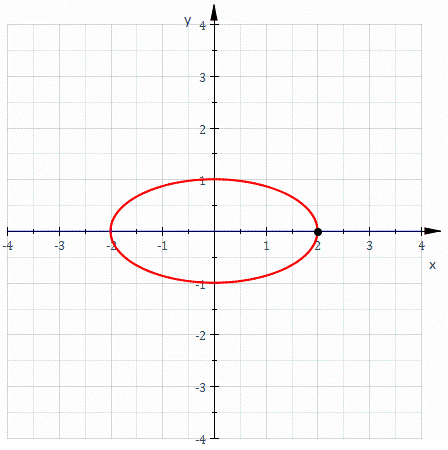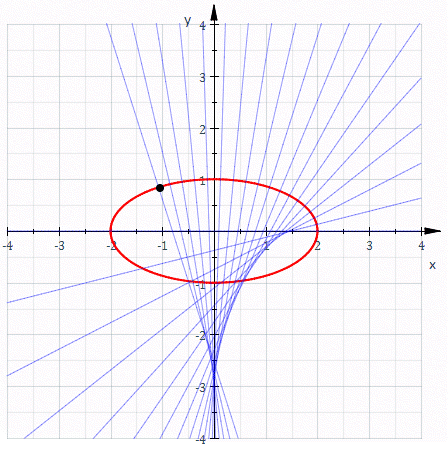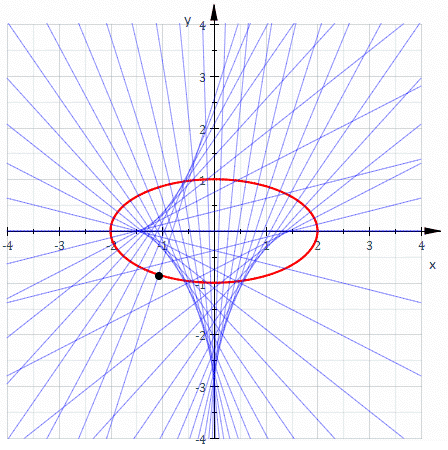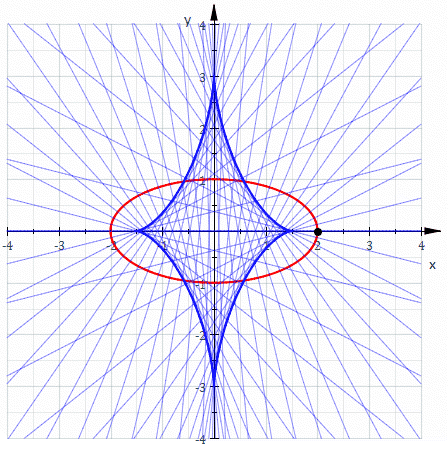
This can be seen in the figure to the right, the blue curve is the evolute of all the other curves. The cusp in the blue curve corresponds to a vertex in the other curves. The cusps in the green curve are on the evolute. Curves with the same evolute are parallel.
Radial curve
A curve with a similar definition is the radial of a given curve. For each point on the curve take the vector from the point to the center of curvature and translate it so that it begins at the origin. Then the locus of points at the end of such vectors is called the radial of the curve. The equation for the radial is obtained by removing the x and y terms from the equation of the evolute. This produces (X, Y) = (−R sinφ, R cosφ) or
Examples
- The evolute of a parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
is a semicubical parabola. The cusp of the latter curve is the center of curvature of the parabola at its vertex.
- The evolute of a logarithmic spiralLogarithmic spiralA logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
is a congruentCongruence (geometry)In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
spiral.
- The evolute of a cycloidCycloidA cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
is a similar cycloid.

