
Cesàro equation
Encyclopedia
In geometry
, the Cesàro equation of a plane curve
is an equation
relating curvature
( ) to arc length
) to arc length
( ). It may also be given as an equation relating the radius of curvature
). It may also be given as an equation relating the radius of curvature
(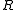 ) to arc length
) to arc length
. (These are equivalent because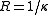 .) Two congruent
.) Two congruent
curves will have the same Cesàro equation. It is named for Ernesto Cesàro
.
Some curves have a particularly simple representation by a Cesàro equation. Some examples are:
The Cesàro equation of a curve is related to its Whewell equation
in the following way, if the Whewell equation
is
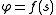
then the Cesàro equation is
 .
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Cesàro equation of a plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
is an equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
relating curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
(
 ) to arc length
) to arc lengthArc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
(
 ). It may also be given as an equation relating the radius of curvature
). It may also be given as an equation relating the radius of curvatureRadius of curvature (mathematics)
In geometry, the radius of curvature, R, of a curve at a point is a measure of the radius of the circular arc which best approximates the curve at that point. If this value taken to be positive when the curve turns anticlockwise and negative when the curve turns clockwise...
(
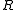 ) to arc length
) to arc lengthArc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
. (These are equivalent because
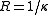 .) Two congruent
.) Two congruentCongruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
curves will have the same Cesàro equation. It is named for Ernesto Cesàro
Ernesto Cesàro
Ernesto Cesàro was an Italian mathematician who worked in the field of differential geometry.Cesàro was born in Naples. He is known also for his 'averaging' method for the summation of divergent series, known as the Cesàro mean.-Books by E. Cesaro:* * Ernesto Cesàro (March 12, 1859 – September...
.
Some curves have a particularly simple representation by a Cesàro equation. Some examples are:
- LineLine (geometry)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
: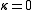 .
. - CircleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
: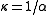 , where
, where  is the radius.
is the radius. - Logarithmic spiralLogarithmic spiralA logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
: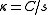 , where
, where 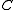 is a constant.
is a constant. - Circle involuteInvoluteIn the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight...
: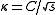 , where
, where 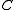 is a constant.
is a constant. - Cornu spiral:
 , where
, where  is a constant.
is a constant. - CatenaryCatenaryIn physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
: .
.
The Cesàro equation of a curve is related to its Whewell equation
Whewell equation
The Whewell equation of a plane curve is an equation that relates the tangential angle with arclength , where the tangential angle is angle between the tangent to the curve and the x-axis and the arc length is the distance along the curve from a fixed point...
in the following way, if the Whewell equation
Whewell equation
The Whewell equation of a plane curve is an equation that relates the tangential angle with arclength , where the tangential angle is angle between the tangent to the curve and the x-axis and the arc length is the distance along the curve from a fixed point...
is
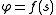
then the Cesàro equation is
 .
.External links
- Curvature Curves at 2dcurves.com.

