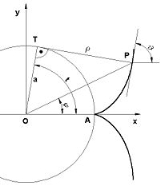
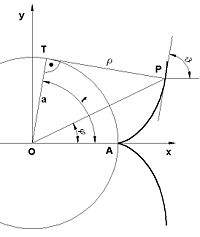
Involute
Encyclopedia
In the differential geometry of curves
, an involute (also known as evolvent) is a curve
obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette
wherein the rolling curve is a straight line containing the generating point. For example, an involute approximates the path followed by a tetherball
as the connecting tether is wound around the center pole. If the center pole has a circular cross-section, then the curve is an involute of a circle.
Alternatively, another way to construct the involute of a curve is to replace the taut string by a line segment
that is tangent to the curve on one end, while the other end traces out the involute. The length of the line segment is changed by an amount equal to the arc length that is traversed on the curve as the tangent point is moved along the curve.
The evolute
of an involute is the original curve, less portions of zero or undefined curvature
. Compare Media:Evolute2.gif and Media:Involute.gif
If function
is a natural parametrization of the curve (i.e., 
for all s), then :
parametrizes the involute.
.
where
is the radius of the circle and 
is a parameter
where
is the radius of the circle and 
is a parameter.
Often a circle involute is found in the form:
.
Leonhard Euler
proposed to use the involute of the circle for the shape of the teeth of toothwheel gear
, a design which is the prevailing one in current use, called involute gear
.
through its vertex
is a tractrix
. In cartesian coordinates the curve follows:
Where: t is a parameter and sech is the hyperbolic secant (1/cosh(x))
Derivative
With
we have
and
.
Substitute
to get
.
is a congruent
cycloid. In cartesian coordinates the curve follows:
Where t is the angle and r is the radius
industry: If two intermeshed gears have teeth with the profile-shape of involutes (rather than, for example, a "classic" triangular shape), they form an involute gear
system. Their relative rates of rotation are constant while the teeth are engaged, and also, the gears always make contact along a single steady line of force. With teeth of other shapes, the relative speeds and forces rise and fall as successive teeth engage, resulting in vibration, noise, and excessive wear. For this reason, nearly all modern gear teeth bear the involute shape.
The involute of a circle is also an important shape in gas compressing
, as a scroll compressor
can be built based on this shape. Scroll compressors make less sound than conventional compressors, and have proven to be quite efficient
.
Differential geometry of curves
Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
, an involute (also known as evolvent) is a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, and involutes....
wherein the rolling curve is a straight line containing the generating point. For example, an involute approximates the path followed by a tetherball
Tetherball
Tetherball is a North American game for two opposing players. The equipment consists of a stationary metal pole, from which is hung a volleyball from a rope, or tether. The two players stand on opposite sides of the pole. Each player tries to hit the ball one way; one clockwise, and one...
as the connecting tether is wound around the center pole. If the center pole has a circular cross-section, then the curve is an involute of a circle.
Alternatively, another way to construct the involute of a curve is to replace the taut string by a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
that is tangent to the curve on one end, while the other end traces out the involute. The length of the line segment is changed by an amount equal to the arc length that is traversed on the curve as the tangent point is moved along the curve.
The evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
of an involute is the original curve, less portions of zero or undefined curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. Compare Media:Evolute2.gif and Media:Involute.gif
If function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is a natural parametrization of the curve (i.e., for all s), then :parametrizes the involute.
Parametric curve
Equations of an involute curve for a parametrically defined function ( x(t) , y(t) ) are:Examples
 |
 |
 |
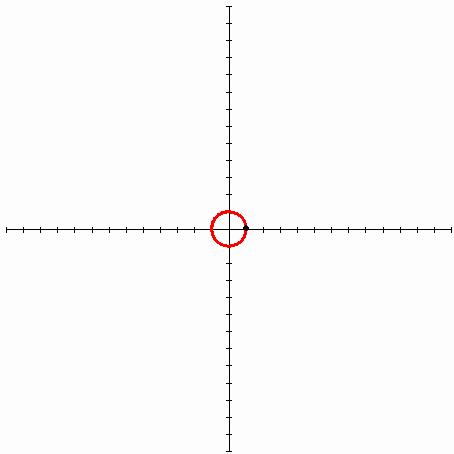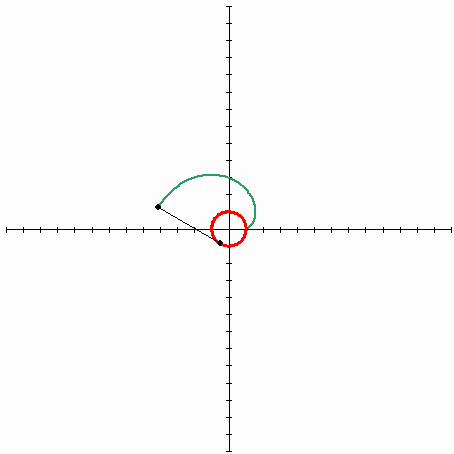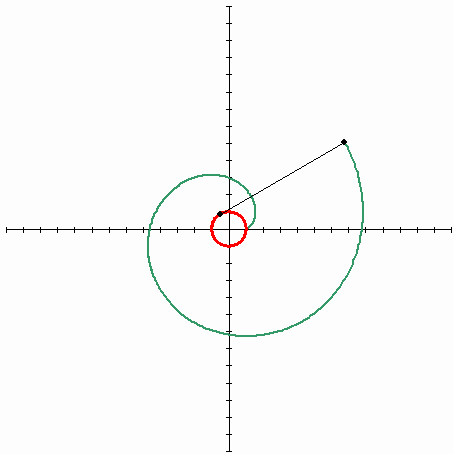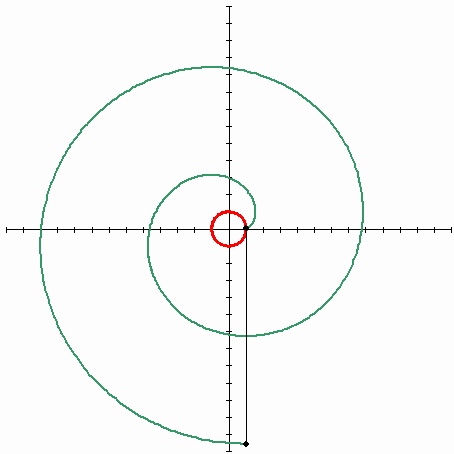
Involute of a circle
The involute of a circle forms a shape which resembles an Archimedean spiralArchimedean spiral
The Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
.
- In Cartesian coordinates the involute of a circle has the parametric equation:
where
is the radius of the circle and is a parameter- In polar coordinates
the involute of a circle has the parametric equation:
where
is the radius of the circle and is a parameter.Often a circle involute is found in the form:
.Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
proposed to use the involute of the circle for the shape of the teeth of toothwheel gear
Gear
A gear is a rotating machine part having cut teeth, or cogs, which mesh with another toothed part in order to transmit torque. Two or more gears working in tandem are called a transmission and can produce a mechanical advantage through a gear ratio and thus may be considered a simple machine....
, a design which is the prevailing one in current use, called involute gear
Involute gear
The involute gear profile is the most commonly used system for gearing today. In an involute gear, the profiles of the teeth are involutes of a circle. In involute gear design contact between a pair of gear teeth occurs...
.
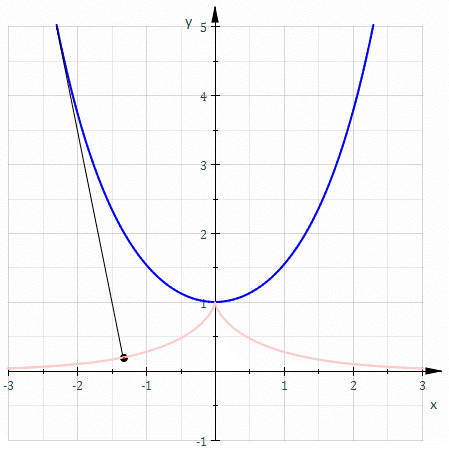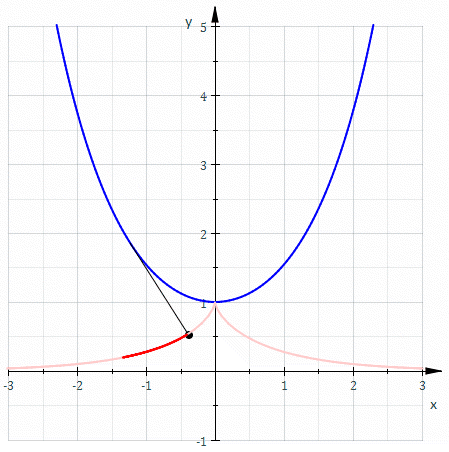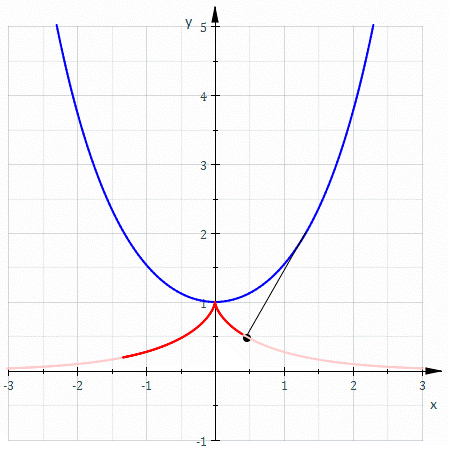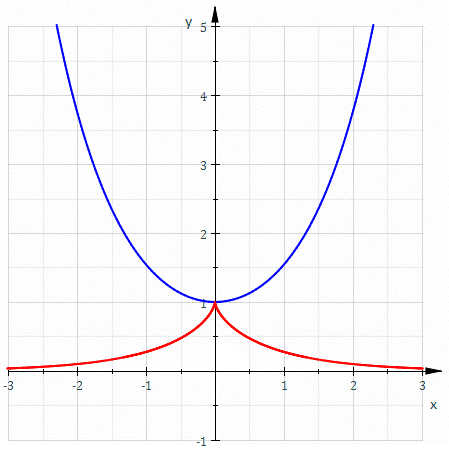
Involute of a catenary
The involute of a catenaryCatenary
In physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
through its vertex
Vertex (curve)
In the geometry of curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant...
is a tractrix
Tractrix
Tractrix is the curve along which a small object moves, under the influence of friction, when pulled on a horizontal plane by a piece of thread and a puller that moves at a right angle to the initial line between the object and the puller at an infinitesimal speed. It is therefore a curve of...
. In cartesian coordinates the curve follows:
Where: t is a parameter and sech is the hyperbolic secant (1/cosh(x))
Derivative
With
we have
and
.Substitute
to get
.Involute of a cycloid
One involute of a cycloidCycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
is a congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
cycloid. In cartesian coordinates the curve follows:
Where t is the angle and r is the radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
Application
The involute has some properties that makes it extremely important to the gearGear
A gear is a rotating machine part having cut teeth, or cogs, which mesh with another toothed part in order to transmit torque. Two or more gears working in tandem are called a transmission and can produce a mechanical advantage through a gear ratio and thus may be considered a simple machine....
industry: If two intermeshed gears have teeth with the profile-shape of involutes (rather than, for example, a "classic" triangular shape), they form an involute gear
Involute gear
The involute gear profile is the most commonly used system for gearing today. In an involute gear, the profiles of the teeth are involutes of a circle. In involute gear design contact between a pair of gear teeth occurs...
system. Their relative rates of rotation are constant while the teeth are engaged, and also, the gears always make contact along a single steady line of force. With teeth of other shapes, the relative speeds and forces rise and fall as successive teeth engage, resulting in vibration, noise, and excessive wear. For this reason, nearly all modern gear teeth bear the involute shape.
The involute of a circle is also an important shape in gas compressing
Gas compressor
A gas compressor is a mechanical device that increases the pressure of a gas by reducing its volume.Compressors are similar to pumps: both increase the pressure on a fluid and both can transport the fluid through a pipe. As gases are compressible, the compressor also reduces the volume of a gas...
, as a scroll compressor
Scroll compressor
A scroll compressor is a device for compressing air or refrigerant...
can be built based on this shape. Scroll compressors make less sound than conventional compressors, and have proven to be quite efficient
Mechanical efficiency
Mechanical efficiency measures the effectiveness of a machine in transforming the energy and power that is input to the device into an output force and movement...
.