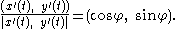Tangential angle
Encyclopedia
In geometry
, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the x-axis. (Note, some authors define the angle as the deviation from the direction of the curve at some fixed starting point. This is equivalent to the definition given here by the addition of a constant to the angle or by rotating the curve.)
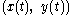, then the tangential angle 
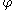at 
is defined (up to a multiple of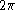 
) by
Thus, the tangential angle specifies the direction of the velocity vector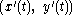
, while the speed specifies its magnitude. The vector 
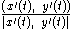is called the unit tangent vector, so an equivalent definition is that the tangential angle at 
is the angle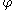 
such that 
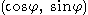is the unit tangent vector at 
.
If the curve is parameterized by arc length
, so 
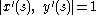, then the definition simplifies to 
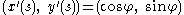. In this case, the curvature
is given by 
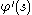, where 
is taken to be positive is the curve bends to the left and negative if the curve bends to the right.
If the curve is given by
, then we may take 
as the parameterization, and we may assume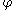 
is between 
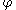and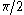 
. This produces the explicit expression 
.
, define the polar tangential angle as the angle between the tangent line to the curve at the given point and ray from the origin to the point. If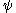
denotes the polar tangential angle, then 
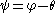, where 
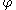is as above and 
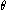is, as usual, the polar angle.
If the curve is defined in polar coordinates by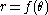
, then polar tangential angle 
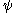at 
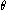is defined (up to a multiple of 
) by
If the curve is parameterized by arc length
as 
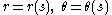, so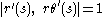 
, then the definition becomes 
.
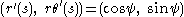The logarithmic spiral
can be defined a curve whose polar tangential angle is constant.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the x-axis. (Note, some authors define the angle as the deviation from the direction of the curve at some fixed starting point. This is equivalent to the definition given here by the addition of a constant to the angle or by rotating the curve.)
Equations
If a curve is given parametrically by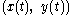, then the tangential angle 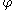at is defined (up to a multiple of 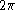) by
Thus, the tangential angle specifies the direction of the velocity vector
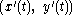, while the speed specifies its magnitude. The vector 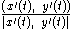is called the unit tangent vector, so an equivalent definition is that the tangential angle at is the angle 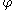such that 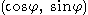is the unit tangent vector at .If the curve is parameterized by arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
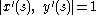, so , then the definition simplifies to 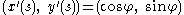. In this case, the curvatureCurvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
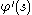is given by , where is taken to be positive is the curve bends to the left and negative if the curve bends to the right.If the curve is given by
, then we may take as the parameterization, and we may assume 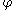is between 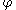and 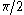. This produces the explicit expression .Polar tangential angle
In polar coordinatesPolar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
, define the polar tangential angle as the angle between the tangent line to the curve at the given point and ray from the origin to the point. If
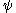denotes the polar tangential angle, then 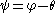, where 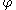is as above and 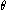is, as usual, the polar angle.If the curve is defined in polar coordinates by
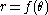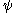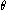, then polar tangential angle at is defined (up to a multiple of ) by-
.
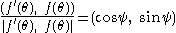If the curve is parameterized by arc length
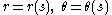as , so 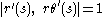, then the definition becomes 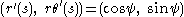.The logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
can be defined a curve whose polar tangential angle is constant.