In computational geometry

Computational geometry

Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...

, the point-in-polygon (PIP) problem asks whether a given point in the plane lies inside, outside, or on the boundary of a polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

. It is a special case of point location

Point location

The point location problem is a fundamental topic of computational geometry. It finds applications in areas that deal with processing geometrical data: computer graphics, geographic information systems , motion planning, and computer aided design ....

 problems and finds applications in areas that deal with processing geometrical data, such as computer graphics

Computer graphics

Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....

, geographical information system

Geographic Information System

A geographic information system, geographical information science, or geospatial information studies is a system designed to capture, store, manipulate, analyze, manage, and present all types of geographically referenced data...

s (GIS), motion planning

Motion planning

Motion planning is a term used in robotics for the process of detailing a task into discrete motions....

, and CAD.

An early description of the problem in computer graphics shows two common approaches (ray casting and angle summation) in use as early as 1974.

An attempt of computer graphics veterans to trace the history of the problem and some tricks for its solution can be found in an issue of the Ray Tracing News.

Ray casting algorithm

One simple way of finding whether the point is inside or outside a simple polygon

Simple polygon

In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....

 is to test how many times a ray, starting from the point and going ANY fixed direction, intersects the edges of the polygon. If the point in question is not on the boundary of the polygon, the number of intersections is an even number if the point is outside, and it is odd if inside. This algorithm is sometimes also known as the crossing number algorithm or the even-odd rule

Even-odd rule

The even–odd rule is an algorithm implemented in vector-based graphic software, like the PostScript language, which determines how a graphical shape with more than one closed outline will be filled...

 algorithm. The algorithm is based on a simple observation that if a point moves along a ray from infinity to the probe point and if it crosses the boundary of a polygon, possibly several times, then it alternately goes from the outside to inside, then from the inside to the outside, etc. As a result, after every two "border crossings" the moving point goes outside. This observation may be mathematically proved using the Jordan curve theorem

Jordan curve theorem

In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...

.

If implemented on a computer with finite precision arithmetics, the results may be incorrect if the point lies very close to that boundary, because of rounding errors. This is not normally a concern, as speed is much more important than complete accuracy in most applications of computer graphics. However, for a formally correct computer program

Computer program

A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...

, one would have to introduce a numerical

Numerical analysis

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....

 tolerance

Tolerance (engineering)

Engineering tolerance is the permissible limit or limits of variation in# a physical dimension,# a measured value or physical property of a material, manufactured object, system, or service,# other measured values ....

 ε and test in line whether P lies within ε of L, in which case the algorithm should stop and report "P lies very close to the boundary."

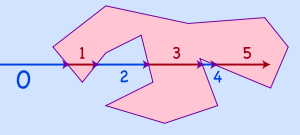
Most implementations of the ray casting algorithm consecutively check intersections of a ray with all sides of the polygon in turn. In this case the following problem must be addressed. If the ray passes exactly through a vertex

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

 of a polygon, then it will intersect 2 segments at their endpoints. While it is OK for the case of the topmost vertex in the example or the vertex between crossing 4 and 5, the case of the rightmost vertex (in the example) requires that we count one intersection for the algorithm to work correctly. A similar problem arises with horizontal segments that happen to fall on the ray. The issue is solved as follows: If the intersection point is a vertex of a tested polygon side, then the intersection counts only if the second vertex of the side lies below the ray. This is effectively equivalent to considering vertices on the ray as lying slightly above the ray.

Once again, the case of the ray passing through a vertex may pose numerical problems in finite precision arithmetics: for two sides adjacent to the same vertex the straightforward computation of the intersection with a ray may not give the vertex in both cases. If the polygon is specified by its vertices, then this problem is eliminated by checking the y-coordinates of the ray and the ends of the tested polygon side before actual computation of the intersection. In other cases, when polygon sides are computed from other types of data, other tricks must be applied for the numerical robustness of the algorithm.

Winding number algorithm

Another algorithm is to compute the given point's winding number

Winding number

In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...

 with respect to the polygon. If the winding number is non-zero, the point lies inside the polygon. One way to compute the winding number is to sum up the angles subtended by each side of the polygon. However, this involves costly inverse trigonometric functions, which generally makes this algorithm slower than the ray casting algorithm. Luckily, these inverse trigonometric functions do not need to be computed. Since the result, the sum of all angles, can add up to 0 or 2*PI (or multiples of 2*PI) only, it is sufficient to track through which quadrants the polygon winds, as it turns around the test point, which makes the winding number algorithm comparable in speed to counting the boundary crossings.

For simple polygons, both algorithms will always give the same results for all points. However, for complex polygons, the algorithms may give different results for points in the regions where the polygon intersects itself, where the polygon does not have a clearly defined inside and outside. In this case, the former algorithm is called the even-odd rule

Even-odd rule

The even–odd rule is an algorithm implemented in vector-based graphic software, like the PostScript language, which determines how a graphical shape with more than one closed outline will be filled...

.

Point in polygon queries

The point in polygon problem may be considered in the general repeated geometric query setting: given a single polygon and a sequence of query points, quickly find the answers for each query point. Clearly, any of the general approaches for planar point location

Point location

The point location problem is a fundamental topic of computational geometry. It finds applications in areas that deal with processing geometrical data: computer graphics, geographic information systems , motion planning, and computer aided design ....

 may be used. Simpler solutions are available for some special polygons.

Special cases

Simpler algorithms are possible for monotone polygon

Monotone polygon

In geometry, a polygon P in the plane is called monotone with respect to a straight line L, if every line orthogonal to L intersects P at most twice....

s, star-shaped polygon

Star-shaped polygon

A star-shaped polygon is a polygonal region in the plane which is a star domain, i.e., a polygon P is star-shaped, if there exists a point z such that for each point p of P the segment zp lies entirely within P.The set of all points z with the described property is called the kernel of...

s and convex polygon

Convex polygon

In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...

s.

External links

• C code to determine if a point is in a polygon
• C code for an algorithm using integers and no divides
• Google Maps Point in Polygon JavaScript extension
• Geometry Engine Open Source (GEOS) based on Java Topology Suite (JTS)
  JTS Topology Suite
  The JTS Topology Suite is an open source Java software library that provides an object model for Euclidean planar linear geometry together with a set of fundamental geometric functions. JTS is primarily intended to be used as a core component of vector-based geomatics software such as...
  
  
• Python Shapely package based on GEOS
• GeoDjango geographic web framework plugin for the Django web framework
• SQL code to determine if a point is in a polygon
• Pascal code to verify if a point is inside a polygon
• Fortran implementation of an improved version of the Nordbeck and Rystedt algorithm