A star-shaped polygon is a polygonal region in the plane which is a star domain

Star domain

In mathematics, a set S in the Euclidean space Rn is called a star domain if there exists x_0 in S such that for all x in S the line segment from x_0 to x is in S...

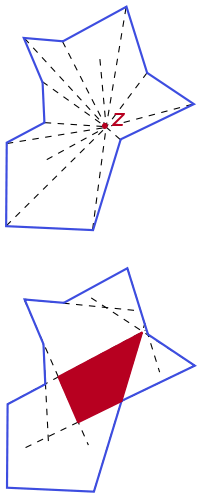
, i.e., a polygon P is star-shaped, if there exists a point z such that for each point p of P the segment zp lies entirely within P.

The set of all points z with the described property is called the kernel of P.

Uses

Star-shaped polygons are of interest in computational geometry

Computational geometry

Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...

 and its applications such as motion planning

Motion planning

Motion planning is a term used in robotics for the process of detailing a task into discrete motions....

 because of its relation to the notion of visibility

Visibility (geometry)

Visibility is a mathematical abstraction of the real-life notion of visibility.Given a set of obstacles in the Euclidean space, two points in the space are said to be visible to each other, if the line segment that joins them does not intersect any obstacles.Computation of visibility is among the...

: the star-shaped polygon may be informally defined as the one whose whole interior is visible from a single point, assuming that the polygon boundary is not transparent.

Properties

Convex polygon

Convex polygon

In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...

s are star shaped, and a convex polygon coincides with its own kernel.

Point-in-polygon queries may be answered in logarithmic time after linear-time preprocessing.

Kernel

Each edge of a polygon defines an interior half-plane, informally defined as a half-plane that contains interior points of the polygon in the vicinity of the edge in question. The kernel of a polygon is the intersection of all its interior half-planes. Intersection of N arbitrary half-planes may be found in Θ

Big O notation

In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...

(N log N) time using the divide and conquer approach. Lee and Preparata presented an algorithm to construct the intersection of interior half-planes in optimal Θ

Big O notation

In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...

(N) time.