Topological quantum number
Encyclopedia
In physics
, a topological quantum number (also called topological charge) is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological
considerations. Most commonly, topological quantum numbers are topological invariants associated with topological defect
s or soliton
-type solutions of some set of differential equation
s modeling a physical system, as the solitons themselves owe their stability to topological considerations. The specific "topological considerations" are usually due to the appearance of the fundamental group
or a higher-dimensional homotopy group
in the description of the problem, quite often because the boundary, on which the boundary conditions are specified, has a non-trivial homotopy group that is preserved by the differential equations. The topological quantum number of a solution is sometimes called the winding number
of the solution, or, more precisely, it is the degree of a continuous mapping
.
Recent ideas about the nature of phase transition
s indicates that topological quantum numbers, and their associated solitons, can be created or destroyed during a phase transition.
, an example is given by the Skyrmion
, for which the baryon number is a topological quantum number. The origin comes from the fact that the isospin
is modelled by SU(2), which is isomorphic to the 3-sphere
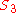and 
inherits the group structure of SU(2) through its bijective association, so the isomorphism is in the category of topological groups. By taking real three-dimensional space, and closing
it with a point at infinity, one also gets a 3-sphere. Solutions to Skyrme's equations in real three dimensional space map a point in "real" (physical; Euclidean) space to a point on the 3-manifold SU(2). Topologically distinct solutions "wrap" the one sphere around the other, such that one solution, no matter how it is deformed, cannot be "unwrapped" without creating a discontinuity in the solution. In physics, such discontinuities are associated with infinite energy, and are thus not allowed.
In the above example, the topological statement is that the 3rd homotopy group of the three sphere is
and so the baryon number can only take on integer values.
A generalization of these ideas is found in the Wess-Zumino-Witten model
.
, the Korteweg–de Vries equation
, and the Ishimori equation
. The one-dimensional sine-Gordon equation makes for a particularly simple example, as the fundamental group at play there is
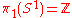
and so is literally a winding number
: a circle can be wrapped around a circle an integer number of times. Quantum sine-Gordon model is equivalent to massive Thirring model
.
Fundamental excitations are fermions: topological quantum number
is the number of fermions. After quantization of sine-Gordon model the topological charge become 'fractional'. Consistent consideration of ultraviolet renormalization
shows that a fractional number of fermions repelled over the ultraviolet cutoff. So the
gets multiplied by a fractional number depending on Plank
constant.
s, such as screw dislocations, can be described by topological solitons. An example includes screw-type dislocations associated with Germanium whiskers.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a topological quantum number (also called topological charge) is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
considerations. Most commonly, topological quantum numbers are topological invariants associated with topological defect
Topological defect
In mathematics and physics, a topological soliton or a topological defect is a solution of a system of partial differential equations or of a quantum field theory homotopically distinct from the vacuum solution; it can be proven to exist because the boundary conditions entail the existence of...
s or soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
-type solutions of some set of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s modeling a physical system, as the solitons themselves owe their stability to topological considerations. The specific "topological considerations" are usually due to the appearance of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
or a higher-dimensional homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
in the description of the problem, quite often because the boundary, on which the boundary conditions are specified, has a non-trivial homotopy group that is preserved by the differential equations. The topological quantum number of a solution is sometimes called the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
of the solution, or, more precisely, it is the degree of a continuous mapping
Degree of a continuous mapping
In topology, the degree is a numerical invariant that describes a continuous mapping between two compact oriented manifolds of the same dimension. Intuitively, the degree represents the number of times that the domain manifold wraps around the range manifold under the mapping...
.
Recent ideas about the nature of phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s indicates that topological quantum numbers, and their associated solitons, can be created or destroyed during a phase transition.
Particle physics
In particle physicsParticle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, an example is given by the Skyrmion
Skyrmion
In theoretical physics, a skyrmion is a mathematical model used to model baryons . It was conceived by Tony Skyrme.-Overview:...
, for which the baryon number is a topological quantum number. The origin comes from the fact that the isospin
Isospin
In physics, and specifically, particle physics, isospin is a quantum number related to the strong interaction. This term was derived from isotopic spin, but the term is confusing as two isotopes of a nucleus have different numbers of nucleons; in contrast, rotations of isospin maintain the number...
is modelled by SU(2), which is isomorphic to the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
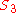and inherits the group structure of SU(2) through its bijective association, so the isomorphism is in the category of topological groups. By taking real three-dimensional space, and closingClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
it with a point at infinity, one also gets a 3-sphere. Solutions to Skyrme's equations in real three dimensional space map a point in "real" (physical; Euclidean) space to a point on the 3-manifold SU(2). Topologically distinct solutions "wrap" the one sphere around the other, such that one solution, no matter how it is deformed, cannot be "unwrapped" without creating a discontinuity in the solution. In physics, such discontinuities are associated with infinite energy, and are thus not allowed.
In the above example, the topological statement is that the 3rd homotopy group of the three sphere is
and so the baryon number can only take on integer values.
A generalization of these ideas is found in the Wess-Zumino-Witten model
Wess-Zumino-Witten model
In theoretical physics and mathematics, the Wess–Zumino–Witten model, also called the Wess–Zumino–Novikov–Witten model, is a simple model of conformal field theory whose solutions are realized by affine Kac–Moody algebras...
.
Exactly solvable models
Additional examples can be found in the domain of exactly solvable models, such as the sine-Gordon equationSine-Gordon equation
The sine–Gordon equation is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d'Alembert operator and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative...
, the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
, and the Ishimori equation
Ishimori equation
The Ishimori equation is a partial differential equation proposed by the Japanese mathematician . Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable .-Equation:The IE has the form...
. The one-dimensional sine-Gordon equation makes for a particularly simple example, as the fundamental group at play there is
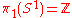
and so is literally a winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
: a circle can be wrapped around a circle an integer number of times. Quantum sine-Gordon model is equivalent to massive Thirring model
Thirring model
The Thirring model is an exactly solvable quantum field theory which describes the self-interactions of a Dirac field in two dimension.-Definition:The Thirring model is given by the Lagrangian density...
.
Fundamental excitations are fermions: topological quantum number
is the number of fermions. After quantization of sine-Gordon model the topological charge become 'fractional'. Consistent consideration of ultraviolet renormalizationRenormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
shows that a fractional number of fermions repelled over the ultraviolet cutoff. So the
gets multiplied by a fractional number depending on PlankPlank
Plank may refer to:*Plank *Plank , an isometric exercise for the abdominal muscles*The Plank , a British comedy film with no dialogue*The Plank , a remake of the 1967 film...
constant.
Solid state physics
In solid state physics, certain types of crystalline dislocationDislocation
In materials science, a dislocation is a crystallographic defect, or irregularity, within a crystal structure. The presence of dislocations strongly influences many of the properties of materials...
s, such as screw dislocations, can be described by topological solitons. An example includes screw-type dislocations associated with Germanium whiskers.
See also
- Inverse scattering transformInverse scattering transformIn mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
- Central chargeCentral chargeIn theoretical physics, a central charge is an operator Z that commutes with all the other symmetry operators. The adjective "central" refers to the center of the symmetry group -- the subgroup of elements that commute with all other elements of the original group—or to the center of a Lie algebra...
- Quantum topologyQuantum topologyQuantum topology is a branch of mathematics that connects quantum mechanics with low-dimensional topology.Dirac notation provides a viewpoint of quantum mechanics which becomes amplified into a framework that can embrace the amplitudes associated with topological spaces and the related embedding of...
- Topological defectTopological defectIn mathematics and physics, a topological soliton or a topological defect is a solution of a system of partial differential equations or of a quantum field theory homotopically distinct from the vacuum solution; it can be proven to exist because the boundary conditions entail the existence of...
- Topological entropy in physics
- Topological orderTopological orderIn physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
- Topological quantum field theoryTopological quantum field theoryA topological quantum field theory is a quantum field theory which computes topological invariants....
- Topological string theoryTopological string theoryIn theoretical physics, topological string theory is a simplified version of string theory. The operators in topological string theory represent the algebra of operators in the full string theory that preserve a certain amount of supersymmetry...