Topological string theory
Encyclopedia
In theoretical physics
, topological string theory is a simplified version of string theory
. The operators in topological string theory represent the algebra
of operators in the full string theory that preserve a certain amount of supersymmetry
. Topological string theory may be obtained by a topological twist of the worldsheet
description of ordinary string theory: the operators are given different spins. The operation is fully analogous to the construction of topological field theory which is a related concept. Consequently, there are no local degrees of freedom in topological string theory.
There are two main versions of topological string theory: the topological A-model and the topological B-model. The results of the calculations in topological string theory generically encode all holomorphic quantities within the full string theory whose values are protected by spacetime
supersymmetry. Various calculations in topological string theory are closely related to Chern-Simons theory
, Gromov-Witten invariant
s, mirror symmetry, and many other topics. As you can see, these are mathematical topics. Indeed, topological string theory cannot be understood as a realistic theory to describe the physical world.
Topological string theory was established and is studied by physicists such as Edward Witten
and Cumrun Vafa
.
N=(1,1) sigma model is defined on each surface. This theory consist of maps from the surface to a supermanifold
. Physically the supermanifold is interpreted as spacetime
and each map is interpreted as the embedding
of the string in spacetime.
Only special spacetimes admit topological strings. Classically one must choose a spacetime such that the theory respects an additional pair of supersymmetries, and so is in fact an N=(2,2) sigma model. This will be the case for example if the spacetime is a Kähler manifold
and the H-flux
is identically equal to zero, although there are more general cases in which the target is a generalized Kähler manifold
and the H-flux is nontrivial.
So far we have described ordinary strings on special backgrounds. These strings are never topological. To make these strings topological, one needs to modify the sigma model via a procedure called a topological twist which was invented by Edward Witten
in 1988. The central observation is that these theories have two U(1) symmetries known as R-symmetries
, and one may modify the Lorentz symmetry by mixing rotation
s and R-symmetries. One may use either of the two R-symmetries, leading to two different theories, called the A model and the B model. After this twist the action of the theory is BRST exact, and as a result the theory has no dynamics, instead all observables depend on the topology of a configuration. Such theories are known as topological theories.
While classically this procedure is always possible, quantum mechanically the U(1) symmetries may be anomalous
. In this case the twisting is not possible. For example, in the Kahler case with H=0 the twist leading to the A-model is always possible but that leading to the B-model is only possible when the first Chern class
of the spacetime vanishes, implying that the spacetime is Calabi-Yau. More generally (2,2) theories have two complex structures and the B model exists when the first Chern classes of associated bundles sum to zero whereas the A model exists when the difference of the Chern classes is zero. In the Kahler case the two complex structures are the same and so the difference is always zero, which is why the A model always exists.
There is no restriction on the number of dimensions of spacetime, other than that it must be even because spacetime is generalized Kahler. However all correlation functions with worldsheets that are not spheres vanish unless the complex dimension of the spacetime is three, and so spacetimes with complex dimension three are the most interesting. This is fortunate for phenomenology, as phenomenological models often use a physical string theory compactified on a 3 complex-dimensional space. The topological string theory is not equivalent to the physical string theory, even on the same space, but certain supersymmetric quantities agree in the two theories.
effects which correct these and yield Gromov-Witten invariant
s, which measure the cup product in a deformed cohomology ring called the quantum cohomology
. The string field theory of the A-model closed strings is known as Kahler gravity, and was introduced by Michael Bershadsky and Vladimir Sadov in Theory of Kahler Gravity.
In addition, there are D2-branes which wrap Lagrangian submanifolds of spacetime. These are submanifolds whose dimensions are one half that of space time, and such that the pullback of the Kahler form to the submanifold vanishes. The worldvolume theory on a stack of N D2-branes is the string field theory of the open strings of the A-model, which is a U(N) Chern-Simons theory
.
The fundamental topological strings may end on the D2-branes. While the embedding of a string depends only on the Kahler form, the embeddings of the branes depends entirely on the complex structure. In particular, when a string ends on a brane the intersection will always be orthogonal, as the wedge product of the Kahler form and the homolomorphic 3-form is zero. In the physical string this is necessary for the stability of the configuration, but here it is a property of Lagrangian and homolomorphic cycles on a Kahler manifold.
Away from the Calabi-Yau case, there may also be coisotropic branes in various dimensions. These were first introduced by Anton Kapustin and Dmitri Orlov in Remarks on A-Branes, Mirror Symmetry, and the Fukaya Category
and Cumrun Vafa
in Kodaira–Spencer Theory of Gravity and Exact Results for Quantum String Amplitudes.
The B-model also comes with D(-1), D1, D3 and D5-branes, which wrap holomorphic 0, 2, 4 and 6-submanifolds respectively. The 6-submanifold is a connected component of the spacetime. The theory on a D5-brane is known as holomorphic Chern-Simons theory. The Lagrangian density is the wedge product of that of ordinary Chern-Simons theory with the holomorphic (3,0)-form, which exists in the Calabi-Yau case. The Lagrangian densities of the theories on the lower-dimensional branes may be obtained from holomorphic Chern-Simons theory by dimensional reductions.
In particular, the D2-branes of the A-model lift to points at which the circle bundle degenerates, or more precisely Kaluza-Klein monopole
s. The fundamental strings of the A-model lift to membranes named M2-branes in topological M-theory.
One special case that has attracted much interest is topological M-theory on a space with G2 holonomy and the A-model on a Calabi-Yau. In this case, the M2-branes wrap associative 3-cycles. Strictly speaking, the topological M-theory conjecture has only been made in this context, as in this case functions introduced by Nigel Hitchin
in The Geometry of Three-Forms in Six and Seven Dimensions and Stable Forms and Special Metrics provide a candidate low energy effective action.
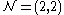supersymmetric
sigma model, the (2,2) supersymmetry means that the fermionic generators of the supersymmetry algebra, called supercharges, may be assembled into a single Dirac spinor, which consists of two Majorana–Weyl spinors of each chirality. This sigma model is topologically twisted, which means that the Lorentz symmetry generators that appear in the supersymmetry algebra simultaneously rotate the physical spacetime and also rotate the fermionic directions via the action of one of the R-symmetries
. The R-symmetry group of a 2-dimensional N=(2,2) field theory is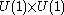
, twists by the two different factors lead to the A and B models respectively. The topological twisted construction of topological string theories was introduced by Edward Witten
in his 1988 paper Topological Sigma Models.
may be written as an anticommutator of a supercharge and another field. As the stress-energy tensor measures the dependence of the action
on the metric tensor
, this implies that all correlation function
s of Q-invariant operators are independent of the metric. In this sense, the theory is topological.
More generally, any D-term
in the action, which is any term which may be expressed as an integral over all of superspace
, is an anticommutator of a supercharge and so does not affect the topological observables. Yet more generally, in the B model any term which may be written as an integral over the fermionic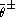
coordinates does not contribute, whereas in the A-model any term which is an integral over 
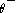or over 
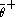does not contribute. This implies that A model observables are independent of the superpotential
(as it may be written as an integral over just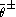
) but depend holomorphically on the twisted superpotential, and vice versa for the B model.
on a three-torus. The A-model and B-model on the same manifold are conjectured to be related by S-duality
, which implies the existence of several new branes, called NS branes by analogy with the NS5-brane
, which wrap the same cycles as the original branes but in the opposite theory. Also a combination of the A-model and a sum of the B-model and its conjugate are related to topological M-theory by a kind of dimensional reduction
. Here the degrees of freedom of the A-model and the B-models appear to not be simultaneously observable, but rather to have a relation similar to that between position and momentum
in quantum mechanics
.
argued that this structure is analogous to a structure that one finds geometrically quantizing
the space of complex structures. Once this space has been quantized, only half of the dimensions simultaneously commute and so the number of degrees of freedom has been halved. This halving depends on an arbitrary choice, called a polarization
. The conjugate model contains the missing degrees of freedom, and so by tensoring the B-model and its conjugate one reobtains all of the missing degrees of freedom and also eliminates the dependence on the arbitrary choice of polarization.
Perhaps the first such duality is the Gopakumar-Vafa duality, which was introduced by Rajesh Gopakumar
and Cumrun Vafa
in On the Gauge Theory/Geometry Correspondence.This relates a stack of N D2-branes on a 3-sphere in the A-model on the deformed conifold
to the closed string theory of the A-model on a resolved conifold with a B field
equal to N times the string coupling constant.
The open strings in the A model are described by a U(N) Chern-Simons theory, while the closed string theory on the A-model is described by the Kahler gravity.
Although the conifold is said to be resolved, the area of the blown up two-sphere is zero, it is only the B-field, which is often considered to be the complex part of the area, which is nonvanishing. In fact, as the Chern-Simons theory is topological, one may shrink the volume of the deformed three-sphere to zero and so
arrive at the same geometry as in the dual theory.
The mirror dual of this duality is another duality, which relates open strings in the B model on a brane wrapping the 2-cycle in the resolved conifold to closed strings in the B model on the deformed conifold. Open strings in the B-model are described by dimensional reductions of homolomorphic Chern-Simons theory on the branes on which they end, while closed strings in the B model are described by Kodaira–Spencer gravity.
, Nicolai Reshetikhin
and Cumrun Vafa
conjectured that the quantum A-model is dual to a classical melting crystal
at a temperature
equal to the inverse of the string coupling constant. This conjecture was interpreted in Quantum Foam and Topological Strings, by Amer Iqbal
, Nikita Nekrasov
, Andrei Okounkov
and Cumrun Vafa
. They claim that the statistical sum over melting crystal configurations is equivalent to a path integral over changes in spacetime topology
supported in small regions with area
of order the product of the string coupling constant and α'.
Such configurations, with spacetime full of many small bubbles, dates back to John Archibald Wheeler
in 1964, but has rarely appeared in string theory
as it is notoriously difficult to make precise. However in this duality the authors are able to cast the dynamics of the quantum foam in the familiar language of a topologically twisted U(1) gauge theory
, whose field strength is linearly related to the Kähler form of the A-model. In particular this suggests that the A-model Kahler form should be quantized.
s in N=1 supersymmetric
gauge theories
in four dimensions. Perturbative A model calculations also count BPS states of spinning black holes in five dimensions.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, topological string theory is a simplified version of string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
. The operators in topological string theory represent the algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
of operators in the full string theory that preserve a certain amount of supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
. Topological string theory may be obtained by a topological twist of the worldsheet
Worldsheet
In string theory, a worldsheet is a two-dimensional manifold which describes the embedding of a string in spacetime. The term was coined by Leonard Susskind around 1967 as a direct generalization of the world line concept for a point particle in special and general relativity.The type of string,...
description of ordinary string theory: the operators are given different spins. The operation is fully analogous to the construction of topological field theory which is a related concept. Consequently, there are no local degrees of freedom in topological string theory.
There are two main versions of topological string theory: the topological A-model and the topological B-model. The results of the calculations in topological string theory generically encode all holomorphic quantities within the full string theory whose values are protected by spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
supersymmetry. Various calculations in topological string theory are closely related to Chern-Simons theory
Chern-Simons theory
The Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type, introduced by Edward Witten. It is so named because its action is proportional to the integral of the Chern–Simons 3-form....
, Gromov-Witten invariant
Gromov-Witten invariant
In mathematics, specifically in symplectic topology and algebraic geometry, Gromov–Witten invariants are rational numbers that, in certain situations, count pseudoholomorphic curves meeting prescribed conditions in a given symplectic manifold...
s, mirror symmetry, and many other topics. As you can see, these are mathematical topics. Indeed, topological string theory cannot be understood as a realistic theory to describe the physical world.
Topological string theory was established and is studied by physicists such as Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
and Cumrun Vafa
Cumrun Vafa
Cumrun Vafa is an Iranian-American leading string theorist from Harvard University where he started as a Harvard Junior Fellow. He is a recipient of the 2008 Dirac Medal.-Birth and education:...
.
Admissible spacetimes
The fundamental strings of string theory are two-dimensional surfaces. A quantum field theory known as theN=(1,1) sigma model is defined on each surface. This theory consist of maps from the surface to a supermanifold
Supermanifold
In physics and mathematics, supermanifolds are generalizations of the manifold concept based on ideas coming from supersymmetry. Several definitions are in use, some of which are described below.- Physics :...
. Physically the supermanifold is interpreted as spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
and each map is interpreted as the embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of the string in spacetime.
Only special spacetimes admit topological strings. Classically one must choose a spacetime such that the theory respects an additional pair of supersymmetries, and so is in fact an N=(2,2) sigma model. This will be the case for example if the spacetime is a Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
and the H-flux
Kalb-Ramond field
In theoretical physics in general and string theory in particular, the Kalb–Ramond field, also known as the NS-NS B-field, is a quantum field that transforms as a two-form i.e. an antisymmetric tensor field with two indices....
is identically equal to zero, although there are more general cases in which the target is a generalized Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
and the H-flux is nontrivial.
So far we have described ordinary strings on special backgrounds. These strings are never topological. To make these strings topological, one needs to modify the sigma model via a procedure called a topological twist which was invented by Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
in 1988. The central observation is that these theories have two U(1) symmetries known as R-symmetries
R-symmetry
In theoretical physics, the R-symmetry is the symmetry transforming different supercharges in a theory with supersymmetry into each other. In the simplest case of the N=1 supersymmetry, such an R-symmetry is isomorphic to a global U group or its discrete subgroup...
, and one may modify the Lorentz symmetry by mixing rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s and R-symmetries. One may use either of the two R-symmetries, leading to two different theories, called the A model and the B model. After this twist the action of the theory is BRST exact, and as a result the theory has no dynamics, instead all observables depend on the topology of a configuration. Such theories are known as topological theories.
While classically this procedure is always possible, quantum mechanically the U(1) symmetries may be anomalous
Anomaly (physics)
In quantum physics an anomaly or quantum anomaly is the failure of a symmetry of a theory's classical action to be a symmetry of any regularization of the full quantum theory. In classical physics an anomaly is the failure of a symmetry to be restored in the limit in which the symmetry-breaking...
. In this case the twisting is not possible. For example, in the Kahler case with H=0 the twist leading to the A-model is always possible but that leading to the B-model is only possible when the first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
of the spacetime vanishes, implying that the spacetime is Calabi-Yau. More generally (2,2) theories have two complex structures and the B model exists when the first Chern classes of associated bundles sum to zero whereas the A model exists when the difference of the Chern classes is zero. In the Kahler case the two complex structures are the same and so the difference is always zero, which is why the A model always exists.
There is no restriction on the number of dimensions of spacetime, other than that it must be even because spacetime is generalized Kahler. However all correlation functions with worldsheets that are not spheres vanish unless the complex dimension of the spacetime is three, and so spacetimes with complex dimension three are the most interesting. This is fortunate for phenomenology, as phenomenological models often use a physical string theory compactified on a 3 complex-dimensional space. The topological string theory is not equivalent to the physical string theory, even on the same space, but certain supersymmetric quantities agree in the two theories.
A-model
The topological A-model comes with a target space which is a 6 real-dimensional generalized Kahler spacetime. In the case in which the spacetime is Kahler, the theory describes two objects. There are fundamental strings, which wrap two real-dimensional holomorphic curves. Amplitudes for the scattering of these strings depend only on the Kahler form of the spacetime, and not on the complex structure. Classically these correlation functions are determined by the cohomology ring. There are quantum mechanical instantonInstanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
effects which correct these and yield Gromov-Witten invariant
Gromov-Witten invariant
In mathematics, specifically in symplectic topology and algebraic geometry, Gromov–Witten invariants are rational numbers that, in certain situations, count pseudoholomorphic curves meeting prescribed conditions in a given symplectic manifold...
s, which measure the cup product in a deformed cohomology ring called the quantum cohomology
Quantum cohomology
In mathematics, specifically in symplectic topology and algebraic geometry, a quantum cohomology ring is an extension of the ordinary cohomology ring of a closed symplectic manifold. It comes in two versions, called small and big; in general, the latter is more complicated and contains more...
. The string field theory of the A-model closed strings is known as Kahler gravity, and was introduced by Michael Bershadsky and Vladimir Sadov in Theory of Kahler Gravity.
In addition, there are D2-branes which wrap Lagrangian submanifolds of spacetime. These are submanifolds whose dimensions are one half that of space time, and such that the pullback of the Kahler form to the submanifold vanishes. The worldvolume theory on a stack of N D2-branes is the string field theory of the open strings of the A-model, which is a U(N) Chern-Simons theory
Chern-Simons theory
The Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type, introduced by Edward Witten. It is so named because its action is proportional to the integral of the Chern–Simons 3-form....
.
The fundamental topological strings may end on the D2-branes. While the embedding of a string depends only on the Kahler form, the embeddings of the branes depends entirely on the complex structure. In particular, when a string ends on a brane the intersection will always be orthogonal, as the wedge product of the Kahler form and the homolomorphic 3-form is zero. In the physical string this is necessary for the stability of the configuration, but here it is a property of Lagrangian and homolomorphic cycles on a Kahler manifold.
Away from the Calabi-Yau case, there may also be coisotropic branes in various dimensions. These were first introduced by Anton Kapustin and Dmitri Orlov in Remarks on A-Branes, Mirror Symmetry, and the Fukaya Category
B-model
The B-model also contains fundamental strings, but their scattering amplitudes depend entirely upon the complex structure and are independent of the Kahler structure. In particular, they are insensitive to worldsheet instanton effects and so can often be calculated exactly. Mirror symmetry then relates them to A model amplitudes, allowing one to compute Gromov-Witten invariants. The string field theory of the closed strings of the B-model is known as the Kodaira–Spencer theory of gravity and was developed by Michael Bershadsky, Sergio Cecotti, Hirosi OoguriHirosi Ooguri
is a theoretical physicist at California Institute of Technology. He is a leading theorist in high energy physics and works at the interface of elementary particle physics, string theory, and related mathematics....
and Cumrun Vafa
Cumrun Vafa
Cumrun Vafa is an Iranian-American leading string theorist from Harvard University where he started as a Harvard Junior Fellow. He is a recipient of the 2008 Dirac Medal.-Birth and education:...
in Kodaira–Spencer Theory of Gravity and Exact Results for Quantum String Amplitudes.
The B-model also comes with D(-1), D1, D3 and D5-branes, which wrap holomorphic 0, 2, 4 and 6-submanifolds respectively. The 6-submanifold is a connected component of the spacetime. The theory on a D5-brane is known as holomorphic Chern-Simons theory. The Lagrangian density is the wedge product of that of ordinary Chern-Simons theory with the holomorphic (3,0)-form, which exists in the Calabi-Yau case. The Lagrangian densities of the theories on the lower-dimensional branes may be obtained from holomorphic Chern-Simons theory by dimensional reductions.
Topological M-theory
Topological M-theory, which enjoys a seven-dimensional spacetime, is not a topological string theory, as it contains no topological strings. However topological M-theory on a circle bundle over a 6-manifold has been conjectured to be equivalent to the topological A-model on that 6-manifold.In particular, the D2-branes of the A-model lift to points at which the circle bundle degenerates, or more precisely Kaluza-Klein monopole
Monopole (mathematics)
In mathematics, a monopole is a connection over a principal bundle G with a section of the associated adjoint bundle. The connection and Higgs field should satisfy the Bogomolnyi equation and be of finite action....
s. The fundamental strings of the A-model lift to membranes named M2-branes in topological M-theory.
One special case that has attracted much interest is topological M-theory on a space with G2 holonomy and the A-model on a Calabi-Yau. In this case, the M2-branes wrap associative 3-cycles. Strictly speaking, the topological M-theory conjecture has only been made in this context, as in this case functions introduced by Nigel Hitchin
Nigel Hitchin
Nigel Hitchin is a British mathematician working in the fields of differential geometry, algebraic geometry, and mathematical physics.-Academic career:...
in The Geometry of Three-Forms in Six and Seven Dimensions and Stable Forms and Special Metrics provide a candidate low energy effective action.
The topological twist
The 2-dimensional worldsheet theory is an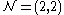 supersymmetricSupersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
sigma model, the (2,2) supersymmetry means that the fermionic generators of the supersymmetry algebra, called supercharges, may be assembled into a single Dirac spinor, which consists of two Majorana–Weyl spinors of each chirality. This sigma model is topologically twisted, which means that the Lorentz symmetry generators that appear in the supersymmetry algebra simultaneously rotate the physical spacetime and also rotate the fermionic directions via the action of one of the R-symmetries
R-symmetry
In theoretical physics, the R-symmetry is the symmetry transforming different supercharges in a theory with supersymmetry into each other. In the simplest case of the N=1 supersymmetry, such an R-symmetry is isomorphic to a global U group or its discrete subgroup...
. The R-symmetry group of a 2-dimensional N=(2,2) field theory is
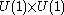, twists by the two different factors lead to the A and B models respectively. The topological twisted construction of topological string theories was introduced by Edward WittenEdward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
in his 1988 paper Topological Sigma Models.
What do the correlators depend on?
The topological twist leads to a topological theory because the stress-energy tensorStress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
may be written as an anticommutator of a supercharge and another field. As the stress-energy tensor measures the dependence of the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
on the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, this implies that all correlation function
Correlation function
A correlation function is the correlation between random variables at two different points in space or time, usually as a function of the spatial or temporal distance between the points...
s of Q-invariant operators are independent of the metric. In this sense, the theory is topological.
More generally, any D-term
D-term
In theoretical physics, one often analyzes theories with supersymmetry in which D-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
in the action, which is any term which may be expressed as an integral over all of superspace
Superspace
"Superspace" has had two meanings in physics. The word was first used by John Wheeler to describe the configuration space of general relativity; for example, this usage may be seen in his famous 1973 textbook Gravitation....
, is an anticommutator of a supercharge and so does not affect the topological observables. Yet more generally, in the B model any term which may be written as an integral over the fermionic
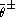coordinates does not contribute, whereas in the A-model any term which is an integral over 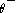or over 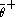does not contribute. This implies that A model observables are independent of the superpotentialSuperpotential
Superpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...
(as it may be written as an integral over just
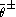) but depend holomorphically on the twisted superpotential, and vice versa for the B model.Dualities between TSTs
A number of dualities relate the above theories. The A-model and B-model on two mirror manifolds are related by mirror symmetry, which has been described as a T-dualityT-duality
T-duality is a symmetry of quantum field theories with differing classical descriptions, of which the relationship between small and large distances in various string theories is a special case. Discussion of the subject originated in a paper by T. S. Buscher and was further developed by Martin...
on a three-torus. The A-model and B-model on the same manifold are conjectured to be related by S-duality
S-duality
In theoretical physics, S-duality is an equivalence of two quantum field theories or string theories. An S-duality transformation maps states and vacua with coupling constant g in one theory to states and vacua with coupling constant 1/g in the dual theory...
, which implies the existence of several new branes, called NS branes by analogy with the NS5-brane
NS5-brane
In theoretical physics, the NS5-brane is a five-dimensional object in string theory that carries a magnetic charge under the B-field, the field under which the fundamental string is electrically charged....
, which wrap the same cycles as the original branes but in the opposite theory. Also a combination of the A-model and a sum of the B-model and its conjugate are related to topological M-theory by a kind of dimensional reduction
Dimensional reduction
In physics, a theory in D spacetime dimensions can be redefined in a lower number of dimensions d, by taking all the fields to be independent of the location in the extra D − d dimensions....
. Here the degrees of freedom of the A-model and the B-models appear to not be simultaneously observable, but rather to have a relation similar to that between position and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
The holomorphic anomaly
The sum of the B-model and its conjugate appears in the above duality because it is the theory whose low energy effective action is expected to be described by Hitchin's formalism. This is because the B-model suffers from a holomorphic anomaly, which states that the dependence on complex quantities, while classically holomorphic, receives nonholomorphic quantum corrections. In Quantum Background Independence in String Theory, Edward WittenEdward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
argued that this structure is analogous to a structure that one finds geometrically quantizing
Geometric quantization
In mathematical physics, geometric quantization is a mathematical approach to defining a quantum theory corresponding to a given classical theory. It attempts to carry out quantization, for which there is in general no exact recipe, in such a way that certain analogies between the classical theory...
the space of complex structures. Once this space has been quantized, only half of the dimensions simultaneously commute and so the number of degrees of freedom has been halved. This halving depends on an arbitrary choice, called a polarization
Polarization
Polarization is a property of certain types of waves that describes the orientation of their oscillations. Electromagnetic waves, such as light, and gravitational waves exhibit polarization; acoustic waves in a gas or liquid do not have polarization because the direction of vibration and...
. The conjugate model contains the missing degrees of freedom, and so by tensoring the B-model and its conjugate one reobtains all of the missing degrees of freedom and also eliminates the dependence on the arbitrary choice of polarization.
Geometric transitions
There are also a number of dualities that relate configurations with D-branes, which are described by open strings, to those with branes the branes replaced by flux and with the geometry described by the near-horizon geometry of the lost branes. The latter are described by closed strings.Perhaps the first such duality is the Gopakumar-Vafa duality, which was introduced by Rajesh Gopakumar
Rajesh Gopakumar
Rajesh Gopakumar is a theoretical physicist at Harish-Chandra Research Institute , Allahabad, India. He hails from the state of Kerala and was the 1987 topper in IIT-JEE.-Career:...
and Cumrun Vafa
Cumrun Vafa
Cumrun Vafa is an Iranian-American leading string theorist from Harvard University where he started as a Harvard Junior Fellow. He is a recipient of the 2008 Dirac Medal.-Birth and education:...
in On the Gauge Theory/Geometry Correspondence.This relates a stack of N D2-branes on a 3-sphere in the A-model on the deformed conifold
Conifold
In mathematics and string theory, a conifold is a generalization of a manifold. Unlike manifolds, conifolds can contain conical singularities i.e. points whose neighbourhoods look like cones over a certain base...
to the closed string theory of the A-model on a resolved conifold with a B field
Kalb-Ramond field
In theoretical physics in general and string theory in particular, the Kalb–Ramond field, also known as the NS-NS B-field, is a quantum field that transforms as a two-form i.e. an antisymmetric tensor field with two indices....
equal to N times the string coupling constant.
The open strings in the A model are described by a U(N) Chern-Simons theory, while the closed string theory on the A-model is described by the Kahler gravity.
Although the conifold is said to be resolved, the area of the blown up two-sphere is zero, it is only the B-field, which is often considered to be the complex part of the area, which is nonvanishing. In fact, as the Chern-Simons theory is topological, one may shrink the volume of the deformed three-sphere to zero and so
arrive at the same geometry as in the dual theory.
The mirror dual of this duality is another duality, which relates open strings in the B model on a brane wrapping the 2-cycle in the resolved conifold to closed strings in the B model on the deformed conifold. Open strings in the B-model are described by dimensional reductions of homolomorphic Chern-Simons theory on the branes on which they end, while closed strings in the B model are described by Kodaira–Spencer gravity.
Crystal melting, quantum foam and U(1) gauge theory
In the paper Quantum Calabi-Yau and Classical Crystals, Andrei OkounkovAndrei Okounkov
Andrei Yuryevich Okounkov is a Russian mathematician who works on representation theory and its applications to algebraic geometry, mathematical physics, probability theory and special functions. He is currently a professor at Columbia University....
, Nicolai Reshetikhin
Nicolai Reshetikhin
Nicolai Yuryevich Reshetikhin is a mathematical physicist, currently a professor of mathematics at the University of California, Berkeley and a professor of mathematical physics at the University of Amsterdam. His research is in the fields of low-dimensional topology, representation theory, and...
and Cumrun Vafa
Cumrun Vafa
Cumrun Vafa is an Iranian-American leading string theorist from Harvard University where he started as a Harvard Junior Fellow. He is a recipient of the 2008 Dirac Medal.-Birth and education:...
conjectured that the quantum A-model is dual to a classical melting crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
at a temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
equal to the inverse of the string coupling constant. This conjecture was interpreted in Quantum Foam and Topological Strings, by Amer Iqbal
Amer Iqbal
Amer Iqbal, Ph.D., is a Pakistani theoretical physicist. He is primarily known for his work in string theory and mathematical physics. He is the associate professor of Physics at the School of Science and Engineering at the Lahore University of Management Sciences...
, Nikita Nekrasov
Nikita Nekrasov
-Background:Nerkrasov was born in Moscow, Russia and attended the Moscow State 57th School, graduating in 1995. He went on to graduate with honors from Moscow Physical Technical Institute in 1995. Nekrasov did his graduate work at Princeton University, receiving his PhD in 1996...
, Andrei Okounkov
Andrei Okounkov
Andrei Yuryevich Okounkov is a Russian mathematician who works on representation theory and its applications to algebraic geometry, mathematical physics, probability theory and special functions. He is currently a professor at Columbia University....
and Cumrun Vafa
Cumrun Vafa
Cumrun Vafa is an Iranian-American leading string theorist from Harvard University where he started as a Harvard Junior Fellow. He is a recipient of the 2008 Dirac Medal.-Birth and education:...
. They claim that the statistical sum over melting crystal configurations is equivalent to a path integral over changes in spacetime topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
supported in small regions with area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of order the product of the string coupling constant and α'.
Such configurations, with spacetime full of many small bubbles, dates back to John Archibald Wheeler
John Archibald Wheeler
John Archibald Wheeler was an American theoretical physicist who was largely responsible for reviving interest in general relativity in the United States after World War II. Wheeler also worked with Niels Bohr in explaining the basic principles behind nuclear fission...
in 1964, but has rarely appeared in string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
as it is notoriously difficult to make precise. However in this duality the authors are able to cast the dynamics of the quantum foam in the familiar language of a topologically twisted U(1) gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
, whose field strength is linearly related to the Kähler form of the A-model. In particular this suggests that the A-model Kahler form should be quantized.
Applications
A-model topological string theory amplitudes are used to compute prepotentials in N=2 supersymmetric gauge theories in four and five dimensions. The amplitudes of the topological B-model, with fluxes and or branes, are used to compute superpotentialSuperpotential
Superpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...
s in N=1 supersymmetric
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
gauge theories
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
in four dimensions. Perturbative A model calculations also count BPS states of spinning black holes in five dimensions.
See also
- Quantum topologyQuantum topologyQuantum topology is a branch of mathematics that connects quantum mechanics with low-dimensional topology.Dirac notation provides a viewpoint of quantum mechanics which becomes amplified into a framework that can embrace the amplitudes associated with topological spaces and the related embedding of...
- Topological defectTopological defectIn mathematics and physics, a topological soliton or a topological defect is a solution of a system of partial differential equations or of a quantum field theory homotopically distinct from the vacuum solution; it can be proven to exist because the boundary conditions entail the existence of...
- Topological entropy in physics
- Topological orderTopological orderIn physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
- Topological quantum field theoryTopological quantum field theoryA topological quantum field theory is a quantum field theory which computes topological invariants....
- Topological quantum numberTopological quantum numberIn physics, a topological quantum number is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations...
- Introduction to M-theoryIntroduction to M-theoryIn non-technical terms, M-theory presents an idea about the basic substance of the universe.-Background:In the early years of the 20th century, the atom – long believed to be the smallest building-block of matter – was proven to consist of even smaller components called protons, neutrons...