Polarization
Encyclopedia
Polarization is a property of certain types of wave
s that describes the orientation of their oscillation
s. Electromagnetic waves, such as light
, and gravitational waves exhibit polarization; acoustic waves (sound
waves) in a gas or liquid do not have polarization because the direction of vibration and direction of propagation are the same.
By convention, the polarization of light is described by specifying the orientation of the wave's electric field
at a point in space over one period of the oscillation. When light travels in free space, in most cases it propagates as a transverse wave
—the polarization is perpendicular to the wave's direction of travel. In this case, the electric field may be oriented in a single direction (linear polarization
), or it may rotate as the wave travels (circular
or elliptical polarization
). In the latter cases, the oscillations can rotate either towards the right or towards the left in the direction of travel. Depending on which rotation is present in a given wave it is called the wave's chirality
or handedness. In general the polarization of an electromagnetic (EM) wave is a complex issue. For instance in a waveguide such as an optical fiber
, or for radially polarized
beams in free space, the description of the wave's polarization is more complicated, as the fields can have longitudinal as well as transverse components. Such EM waves are either TM or hybrid modes
.
For longitudinal wave
s such as sound waves in fluid
s, the direction of oscillation is by definition along the direction of travel, so there is no polarization. In a solid
medium, however, sound waves can be transverse. In this case, the polarization is associated with the direction of the shear stress
in the plane perpendicular to the propagation direction. This is important in seismology
.
Polarization is significant in areas of science and technology dealing with wave propagation
, such as optics
, seismology
, telecommunications and radar
science. The polarization of light can be measured with a polarimeter
. A polarizer
is a device that affects polarization.
, which is a good approximation of most light waves (a plane wave is a wave with infinitely long and wide wavefront
s). For plane waves Maxwell's equations
, specifically Gauss's laws, impose the transversality requirement that the electric
and magnetic field
be perpendicular to the direction of propagation and to each other. Conventionally, when considering polarization, the electric field vector is described and the magnetic field is ignored since it is perpendicular
to the electric field and proportional to it. The electric field vector of a plane wave may be arbitrarily divided into two perpendicular components labeled x and y (with z indicating the direction of travel). For a simple harmonic wave
, where the amplitude of the electric vector varies in a sinusoidal manner in time, the two components have exactly the same frequency. However, these components have two other defining characteristics that can differ. First, the two components may not have the same amplitude
. Second, the two components may not have the same phase
, that is they may not reach their maxima and minima at the same time. Mathematically, the electric field of a plane wave can be written as,
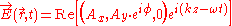
or alternatively,
where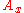
and 
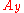are the amplitudes of the x and y directions and 
is the relative phase between the two components.
) is a description of the polarization state. The following figures show some examples of the evolution of the electric field vector (black), with time(the vertical axes), at a particular point in space, along with its x and y components (red/left and blue/right), and the path traced by the tip of the vector in the plane (yellow in figure 1&3, purple in figure 2): The same evolution would occur when looking at the electric field at a particular time while evolving the point in space, along the direction opposite to propagation.
In the leftmost figure above, the two orthogonal (perpendicular) components are in phase. In this case the ratio of the strengths of the two components is constant, so the direction of the electric vector (the vector sum of these two components) is constant. Since the tip of the vector traces out a single line in the plane, this special case is called linear polarization
. The direction of this line depends on the relative amplitudes of the two components.
In the middle figure, the two orthogonal components have exactly the same amplitude and are exactly ninety degrees out of phase. In this case one component is zero when the other component is at maximum or minimum amplitude. There are two possible phase relationships that satisfy this requirement: the x component can be ninety degrees ahead of the y component or it can be ninety degrees behind the y component. In this special case the electric vector traces out a circle in the plane, so this special case is called circular polarization
. The direction the field rotates in depends on which of the two phase relationships exists. These cases are called right-hand circular polarization and left-hand circular polarization, depending on which way the electric vector rotates and the chosen convention.
Another case is when the two components are not in phase and either do not have the same amplitude or are not ninety degrees out of phase, though their phase offset and their amplitude ratio are constant. This kind of polarization is called elliptical polarization
because the electric vector traces out an ellipse
in the plane (the polarization ellipse). This is shown in the above figure on the right.
The "Cartesian" decomposition of the electric field into x and y components is, of course, arbitrary. Plane waves of any polarization can be described instead by combining any two orthogonally
polarized waves, for instance waves of opposite circular polarization. The Cartesian polarization decomposition is natural when dealing with reflection from surfaces, birefringent
materials, or synchrotron radiation
. The circularly polarized modes are a more useful basis for the study of light propagation in stereoisomers.
Though this section discusses polarization for idealized plane waves, all the above is a very accurate description for most practical optical experiments which use TEM modes
, including Gaussian optics.
contain a large number of atoms or molecules that emit light. The orientation of the electric fields produced by these emitters may not be correlated, in which case the light is said to be unpolarized. If there is partial correlation between the emitters, the light is partially polarized. If the polarization is consistent across the spectrum of the source, partially polarized light can be described as a superposition of a completely unpolarized component, and a completely polarized one. One may then describe the light in terms of the degree of polarization
, and the parameters of the polarization ellipse.
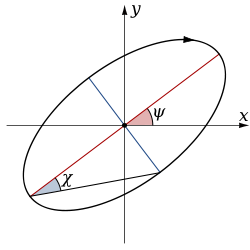For ease of visualization, polarization states are often specified in terms of the polarization ellipse, specifically its orientation and elongation. A common parameterization uses the orientation angle, ψ, the angle between the major semi-axis of the ellipse and the x-axis (also known as tilt angle or azimuth angle) and the ellipticity, ε, the major-to-minor-axis ratio (also known as the axial ratio
). An ellipticity of zero or infinity corresponds to linear polarization and an ellipticity of 1 corresponds to circular polarization. The ellipticity angle, χ = arccot ε= arctan 1/ε, is also commonly used. An example is shown in the diagram to the right. An alternative to the ellipticity or ellipticity angle is the eccentricity
, however unlike the azimuth angle and ellipticity angle, the latter has no obvious geometrical interpretation in terms of the Poincaré sphere (see below).
Full information on a completely polarized state is also provided by the amplitude and phase of oscillations in two components of the electric field vector in the plane of polarization. This representation was used above to show how different states of polarization are possible. The amplitude and phase information can be conveniently represented as a two-dimensional complex
vector (the Jones vector
):
Here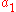
and 
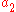denote the amplitude of the wave in the two components of the electric field vector, while 
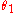and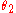 
represent the phases. The product of a Jones vector with a complex number of unit modulus
gives a different Jones vector representing the same ellipse, and thus the same state of polarization. The physical electric field, as the real part of the Jones vector, would be altered but the polarization state itself is independent of absolute phase
. The basis
vectors used to represent the Jones vector need not represent linear polarization states (i.e. be real). In general any two orthogonal states can be used, where an orthogonal vector pair is formally defined as one having a zero inner product. A common choice is left and right circular polarizations, for example to model the different propagation of waves in two such components in circularly birefringent media (see below) or signal paths of coherent detectors sensitive to circular polarization.
Regardless of whether polarization ellipses are represented using geometric parameters or Jones vectors, implicit in the parameterization is the orientation of the coordinate frame. This permits a degree of freedom, namely rotation about the propagation direction. When considering light that is propagating parallel to the surface of the Earth, the terms "horizontal" and "vertical" polarization are often used, with the former being associated with the first component of the Jones vector, or zero azimuth angle. On the other hand, in astronomy
the equatorial coordinate system
is generally used instead, with the zero azimuth (or position angle, as it is more commonly called in astronomy to avoid confusion with the horizontal coordinate system
) corresponding to due north.
for perpendicular). Light with a p-like electric field is said to be p-polarized, pi-polarized, tangential plane polarized, or is said to be a transverse-magnetic (TM) wave. Light with an s-like electric field is s-polarized, also known as sigma-polarized or sagittal plane polarized, or it can be called a transverse-electric (TE) wave. However, there is no universal convention in this TE and TM naming scheme, and certain authors do refer to light with p-like electric field as TE and light with s-like electric field as TM.
, and only statistical information can be gathered about the variations and correlations between components of the electric field. This information is embodied in the coherency matrix
:
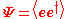
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s that describes the orientation of their oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
s. Electromagnetic waves, such as light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
, and gravitational waves exhibit polarization; acoustic waves (sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
waves) in a gas or liquid do not have polarization because the direction of vibration and direction of propagation are the same.
By convention, the polarization of light is described by specifying the orientation of the wave's electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
at a point in space over one period of the oscillation. When light travels in free space, in most cases it propagates as a transverse wave
Transverse wave
A transverse wave is a moving wave that consists of oscillations occurring perpendicular to the direction of energy transfer...
—the polarization is perpendicular to the wave's direction of travel. In this case, the electric field may be oriented in a single direction (linear polarization
Linear polarization
In electrodynamics, linear polarization or plane polarization of electromagnetic radiation is a confinement of the electric field vector or magnetic field vector to a given plane along the direction of propagation...
), or it may rotate as the wave travels (circular
Circular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
or elliptical polarization
Elliptical polarization
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation...
). In the latter cases, the oscillations can rotate either towards the right or towards the left in the direction of travel. Depending on which rotation is present in a given wave it is called the wave's chirality
Chirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
or handedness. In general the polarization of an electromagnetic (EM) wave is a complex issue. For instance in a waveguide such as an optical fiber
Optical fiber
An optical fiber is a flexible, transparent fiber made of a pure glass not much wider than a human hair. It functions as a waveguide, or "light pipe", to transmit light between the two ends of the fiber. The field of applied science and engineering concerned with the design and application of...
, or for radially polarized
Radial polarisation
A beam of light has radial polarization if at every position in the beam the polarization vector points towards the centre of the beam. In practice, an array of waveplates may be used to provide an approximation to a radially polarized beam...
beams in free space, the description of the wave's polarization is more complicated, as the fields can have longitudinal as well as transverse components. Such EM waves are either TM or hybrid modes
Transverse mode
A transverse mode of a beam of electromagnetic radiation is a particular electromagnetic field pattern of radiation measured in a plane perpendicular to the propagation direction of the beam...
.
For longitudinal wave
Longitudinal wave
Longitudinal waves, as known as "l-waves", are waves that have the same direction of vibration as their direction of travel, which means that the movement of the medium is in the same direction as or the opposite direction to the motion of the wave. Mechanical longitudinal waves have been also...
s such as sound waves in fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s, the direction of oscillation is by definition along the direction of travel, so there is no polarization. In a solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...
medium, however, sound waves can be transverse. In this case, the polarization is associated with the direction of the shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
in the plane perpendicular to the propagation direction. This is important in seismology
Seismology
Seismology is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. The field also includes studies of earthquake effects, such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, oceanic,...
.
Polarization is significant in areas of science and technology dealing with wave propagation
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
, such as optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, seismology
Seismology
Seismology is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. The field also includes studies of earthquake effects, such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, oceanic,...
, telecommunications and radar
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
science. The polarization of light can be measured with a polarimeter
Polarimeter
A polarimeter is a scientific instrument used to measure the angle of rotation caused by passing polarized light through an optically active substance....
. A polarizer
Polarizer
A polarizer is an optical filter that passes light of a specific polarization and blocks waves of other polarizations. It can convert a beam of light of undefined or mixed polarization into a beam with well-defined polarization. The common types of polarizers are linear polarizers and circular...
is a device that affects polarization.
Basics: plane waves
The simplest manifestation of polarization to visualize is that of a plane wavePlane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
, which is a good approximation of most light waves (a plane wave is a wave with infinitely long and wide wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
s). For plane waves Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, specifically Gauss's laws, impose the transversality requirement that the electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
be perpendicular to the direction of propagation and to each other. Conventionally, when considering polarization, the electric field vector is described and the magnetic field is ignored since it is perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the electric field and proportional to it. The electric field vector of a plane wave may be arbitrarily divided into two perpendicular components labeled x and y (with z indicating the direction of travel). For a simple harmonic wave
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
, where the amplitude of the electric vector varies in a sinusoidal manner in time, the two components have exactly the same frequency. However, these components have two other defining characteristics that can differ. First, the two components may not have the same amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
. Second, the two components may not have the same phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
, that is they may not reach their maxima and minima at the same time. Mathematically, the electric field of a plane wave can be written as,
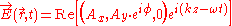
or alternatively,
where
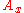and 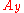are the amplitudes of the x and y directions and is the relative phase between the two components.Polarization state
The shape traced out in a fixed plane by the electric vector as such a plane wave passes over it (a Lissajous figureLissajous curve
In mathematics, a Lissajous curve , also known as Lissajous figure or Bowditch curve, is the graph of a system of parametric equationswhich describe complex harmonic motion...
) is a description of the polarization state. The following figures show some examples of the evolution of the electric field vector (black), with time(the vertical axes), at a particular point in space, along with its x and y components (red/left and blue/right), and the path traced by the tip of the vector in the plane (yellow in figure 1&3, purple in figure 2): The same evolution would occur when looking at the electric field at a particular time while evolving the point in space, along the direction opposite to propagation.
In the leftmost figure above, the two orthogonal (perpendicular) components are in phase. In this case the ratio of the strengths of the two components is constant, so the direction of the electric vector (the vector sum of these two components) is constant. Since the tip of the vector traces out a single line in the plane, this special case is called linear polarization
Linear polarization
In electrodynamics, linear polarization or plane polarization of electromagnetic radiation is a confinement of the electric field vector or magnetic field vector to a given plane along the direction of propagation...
. The direction of this line depends on the relative amplitudes of the two components.
In the middle figure, the two orthogonal components have exactly the same amplitude and are exactly ninety degrees out of phase. In this case one component is zero when the other component is at maximum or minimum amplitude. There are two possible phase relationships that satisfy this requirement: the x component can be ninety degrees ahead of the y component or it can be ninety degrees behind the y component. In this special case the electric vector traces out a circle in the plane, so this special case is called circular polarization
Circular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
. The direction the field rotates in depends on which of the two phase relationships exists. These cases are called right-hand circular polarization and left-hand circular polarization, depending on which way the electric vector rotates and the chosen convention.
Another case is when the two components are not in phase and either do not have the same amplitude or are not ninety degrees out of phase, though their phase offset and their amplitude ratio are constant. This kind of polarization is called elliptical polarization
Elliptical polarization
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation...
because the electric vector traces out an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
in the plane (the polarization ellipse). This is shown in the above figure on the right.
The "Cartesian" decomposition of the electric field into x and y components is, of course, arbitrary. Plane waves of any polarization can be described instead by combining any two orthogonally
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
polarized waves, for instance waves of opposite circular polarization. The Cartesian polarization decomposition is natural when dealing with reflection from surfaces, birefringent
Birefringence
Birefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
materials, or synchrotron radiation
Synchrotron radiation
The electromagnetic radiation emitted when charged particles are accelerated radially is called synchrotron radiation. It is produced in synchrotrons using bending magnets, undulators and/or wigglers...
. The circularly polarized modes are a more useful basis for the study of light propagation in stereoisomers.
Though this section discusses polarization for idealized plane waves, all the above is a very accurate description for most practical optical experiments which use TEM modes
Transverse mode
A transverse mode of a beam of electromagnetic radiation is a particular electromagnetic field pattern of radiation measured in a plane perpendicular to the propagation direction of the beam...
, including Gaussian optics.
Unpolarized light
Most sources of electromagnetic radiationElectromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
contain a large number of atoms or molecules that emit light. The orientation of the electric fields produced by these emitters may not be correlated, in which case the light is said to be unpolarized. If there is partial correlation between the emitters, the light is partially polarized. If the polarization is consistent across the spectrum of the source, partially polarized light can be described as a superposition of a completely unpolarized component, and a completely polarized one. One may then describe the light in terms of the degree of polarization
Degree of polarization
Degree of polarization is a quantity used to describe the portion of an electromagnetic wave which is polarized. A perfectly polarized wave has a DOP of 100%, whereas an unpolarized wave has a DOP of 0%. A wave which is partially polarized, and therefore can be represented by a superposition of...
, and the parameters of the polarization ellipse.
Parameterization
Axial ratio
Axial ratio, for any structure or shape with two or more axes, is the ratio of the length of those axes to each other - the longer axis divided by the shorter....
). An ellipticity of zero or infinity corresponds to linear polarization and an ellipticity of 1 corresponds to circular polarization. The ellipticity angle, χ = arccot ε= arctan 1/ε, is also commonly used. An example is shown in the diagram to the right. An alternative to the ellipticity or ellipticity angle is the eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
, however unlike the azimuth angle and ellipticity angle, the latter has no obvious geometrical interpretation in terms of the Poincaré sphere (see below).
Full information on a completely polarized state is also provided by the amplitude and phase of oscillations in two components of the electric field vector in the plane of polarization. This representation was used above to show how different states of polarization are possible. The amplitude and phase information can be conveniently represented as a two-dimensional complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
vector (the Jones vector
Jones calculus
In optics, polarized light can be described using the Jones calculus, invented by R. C. Jones in 1941. Polarized light is represented by a Jones vector, and linear optical elements are represented by Jones matrices...
):
Here
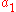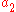and denote the amplitude of the wave in the two components of the electric field vector, while 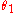and 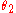represent the phases. The product of a Jones vector with a complex number of unit modulusAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
gives a different Jones vector representing the same ellipse, and thus the same state of polarization. The physical electric field, as the real part of the Jones vector, would be altered but the polarization state itself is independent of absolute phase
Absolute phase
Absolute phase refers to the phase of a waveform relative to some standard . To the extent that this standard is accepted by all parties, one can speak of an absolute phase in a particular field of application....
. The basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
vectors used to represent the Jones vector need not represent linear polarization states (i.e. be real). In general any two orthogonal states can be used, where an orthogonal vector pair is formally defined as one having a zero inner product. A common choice is left and right circular polarizations, for example to model the different propagation of waves in two such components in circularly birefringent media (see below) or signal paths of coherent detectors sensitive to circular polarization.
Regardless of whether polarization ellipses are represented using geometric parameters or Jones vectors, implicit in the parameterization is the orientation of the coordinate frame. This permits a degree of freedom, namely rotation about the propagation direction. When considering light that is propagating parallel to the surface of the Earth, the terms "horizontal" and "vertical" polarization are often used, with the former being associated with the first component of the Jones vector, or zero azimuth angle. On the other hand, in astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
the equatorial coordinate system
Equatorial coordinate system
The equatorial coordinate system is a widely-used method of mapping celestial objects. It functions by projecting the Earth's geographic poles and equator onto the celestial sphere. The projection of the Earth's equator onto the celestial sphere is called the celestial equator...
is generally used instead, with the zero azimuth (or position angle, as it is more commonly called in astronomy to avoid confusion with the horizontal coordinate system
Horizontal coordinate system
The horizontal coordinate system is a celestial coordinate system that uses the observer's local horizon as the fundamental plane. This coordinate system divides the sky into the upper hemisphere where objects are visible, and the lower hemisphere where objects cannot be seen since the earth is in...
) corresponding to due north.
S and P Polarization
Another coordinate system frequently used relates to the plane made by the propagation direction and a vector perpendicular to the plane of a reflecting surface. This is known as the plane of incidence. The component of the electric field parallel to this plane is termed p-like (parallel) and the component perpendicular to this plane is termed s-like (from senkrecht, GermanGerman language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
for perpendicular). Light with a p-like electric field is said to be p-polarized, pi-polarized, tangential plane polarized, or is said to be a transverse-magnetic (TM) wave. Light with an s-like electric field is s-polarized, also known as sigma-polarized or sagittal plane polarized, or it can be called a transverse-electric (TE) wave. However, there is no universal convention in this TE and TM naming scheme, and certain authors do refer to light with p-like electric field as TE and light with s-like electric field as TM.
Parameterization of incoherent or partially polarized radiation
In the case of partially-polarized radiation, the Jones vector varies in time and space in a way that differs from the constant rate of phase rotation of monochromatic, purely-polarized waves. In this case, the wave field is likely stochasticStochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
, and only statistical information can be gathered about the variations and correlations between components of the electric field. This information is embodied in the coherency matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
:
-
-
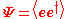
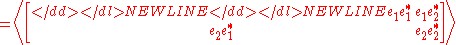
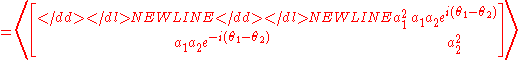
where angular brackets denote averaging over many wave cycles. Several variants of the coherency matrix have been proposed: the WienerNorbert WienerNorbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
coherency matrix and the spectral coherency matrix of Richard Barakat measure the coherence of a spectral decomposition of the signal, while the WolfEmil WolfEmil Wolf is a Czech born American physicist who made advancements in physical optics, including diffraction, coherence properties of optical fields, spectroscopy of partially coherent radiation, and the theory of direct scattering and inverse scattering. He is also the author of several works on...
coherency matrix averages over all time/frequencies.
The coherency matrix contains all second order statistical information about the polarization. This matrix can be decomposed into the sum of two idempotent matrices, corresponding to the eigenvectors of the coherency matrix, each representing a polarization state that is orthogonal to the other. An alternative decomposition is into completely polarized (zero determinant) and unpolarized (scaled identity matrix) components. In either case, the operation of summing the components corresponds to the incoherent superposition of waves from the two components. The latter case gives rise to the concept of the "degree of polarization"; i.e., the fraction of the total intensity contributed by the completely polarized component.
The coherency matrix is not easy to visualize, and it is therefore common to describe incoherent or partially polarized radiation in terms of its total intensity (I), (fractional) degree of polarization (p), and the shape parameters of the polarization ellipse. An alternative and mathematically convenient description is given by the Stokes parametersStokes parametersThe Stokes parameters are a set of values that describe the polarization state of electromagnetic radiation. They were defined by George Gabriel Stokes in 1852, as a mathematically convenient alternative to the more common description of incoherent or partially polarized radiation in terms of its...
, introduced by George Gabriel StokesGeorge Gabriel StokesSir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
in 1852. The relationship of the Stokes parameters to intensity and polarization ellipse parameters is shown in the equations and figure below.
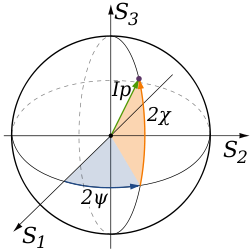
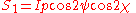
Here Ip, 2ψ and 2χ are the spherical coordinates of the polarization state in the three-dimensional space of the last three Stokes parameters. Note the factors of two before ψ and χ corresponding respectively to the facts that any polarization ellipse is indistinguishable from one rotated by 180°, or one with the semi-axis lengths swapped accompanied by a 90° rotation. The Stokes parameters are sometimes denoted I, Q, U and V.
The Stokes parameters contain all of the information of the coherency matrix, and are related to it linearly by means of the identity matrix plus the three Pauli matricesPauli matricesThe Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
:
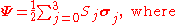
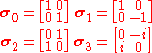
Mathematically, the factor of two relating physical angles to their counterparts in Stokes space derives from the use of second-order moments and correlations, and incorporates the loss of information due to absolute phase invariance.
The figure above makes use of a convenient representation of the last three Stokes parameters as components in a three-dimensional vector space. This space is closely related to the Poincaré sphere, which is the spherical surface occupied by completely polarized states in the space of the vector
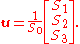
All four Stokes parameters can also be combined into the four-dimensional Stokes vector, which can be interpreted as four-vectorFour-vectorIn the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
s of Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. In this case, all physically realizable polarization states correspond to time-like, future-directed vectors.
Propagation, reflection and scattering
In a vacuumVacuumIn everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
, the components of the electric field propagate at the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, so that the phase of the wave varies in space and time while the polarization state does not. That is,
where k is the wavenumberWavenumberIn the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
and positive z is the direction of propagation. As noted above, the physical electric vector is the real part of the Jones vector. When electromagnetic waves interact with matter, their propagation is altered. If this depends on the polarization states of the waves, then their polarization may also be altered.
In many types of media, electromagnetic waves may be decomposed into two orthogonal components that encounter different propagation effects. A similar situation occurs in the signal processing paths of detection systems that record the electric field directly. Such effects are most easily characterized in the form of a complex 2×2 transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
matrix called the Jones matrixJones calculusIn optics, polarized light can be described using the Jones calculus, invented by R. C. Jones in 1941. Polarized light is represented by a Jones vector, and linear optical elements are represented by Jones matrices...
:
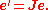
In general the Jones matrix of a medium depends on the frequency of the waves.
For propagation effects in two orthogonal modes, the Jones matrix can be written as
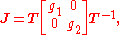
where g1 and g2 are complex numbers representing the change in amplitude and phase caused in each of the two propagation modes, and T is a unitary matrix representing a change of basis from these propagation modes to the linear system used for the Jones vectors. For those media in which the amplitudes are unchanged but a differential phase delay occurs, the Jones matrix is unitary, while those affecting amplitude without phase have Hermitian Jones matrices. In fact, since any matrix may be written as the product of unitary and positive Hermitian matrices, any sequence of linear propagation effects, no matter how complex, can be written as the product of these two basic types of transformations.
Media in which the two modes accrue a differential delay are called birefringentBirefringenceBirefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
. Well known manifestations of this effect appear in optical wave plateWave plateA wave plate or retarder is an optical device that alters the polarization state of a light wave travelling through it.- Operation :A wave plate works by shifting the phase between two perpendicular polarization components of the light wave. A typical wave plate is simply a birefringent crystal...
s/retarders (linear modes) and in Faraday rotation/optical rotationOptical rotationOptical rotation is the turning of the plane of linearly polarized light about the direction of motion as the light travels through certain materials. It occurs in solutions of chiral molecules such as sucrose , solids with rotated crystal planes such as quartz, and spin-polarized gases of atoms...
(circular modes). An easily visualized example is one where the propagation modes are linear, and the incoming radiation is linearly polarized at a 45° angle to the modes. As the phase difference starts to appear, the polarization becomes elliptical, eventually changing to purely circular polarization (90° phase difference), then to elliptical and eventually linear polarization (180° phase) with an azimuth angle perpendicular to the original direction, then through circular again (270° phase), then elliptical with the original azimuth angle, and finally back to the original linearly polarized state (360° phase) where the cycle begins anew. In general the situation is more complicated and can be characterized as a rotation in the Poincaré sphere about the axis defined by the propagation modes (this is a consequence of the isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of SU(2) with SO(3)). Examples for linear (blue), circular (red), and elliptical (yellow) birefringenceBirefringenceBirefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
are shown in the figure on the left. The total intensity and degree of polarization are unaffected. If the path length in the birefringent medium is sufficient, plane waves will exit the material with a significantly different propagation direction, due to refractionRefractionRefraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
. For example, this is the case with macroscopic crystalCrystalA crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s of calciteCalciteCalcite is a carbonate mineral and the most stable polymorph of calcium carbonate . The other polymorphs are the minerals aragonite and vaterite. Aragonite will change to calcite at 380-470°C, and vaterite is even less stable.-Properties:...
, which present the viewer with two offset, orthogonally polarized images of whatever is viewed through them. It was this effect that provided the first discovery of polarization, by Erasmus Bartholinus in 1669. In addition, the phase shift, and thus the change in polarization state, is usually frequency dependent, which, in combination with dichroismDichroismDichroism has two related but distinct meanings in optics. A dichroic material is either one which causes visible light to be split up into distinct beams of different wavelengths , or one in which light rays having different polarizations are absorbed by different amounts.The original meaning of...
, often gives rise to bright colors and rainbow-like effects.
Media in which the amplitude of waves propagating in one of the modes is reduced are called dichroicDichroismDichroism has two related but distinct meanings in optics. A dichroic material is either one which causes visible light to be split up into distinct beams of different wavelengths , or one in which light rays having different polarizations are absorbed by different amounts.The original meaning of...
. Devices that block nearly all of the radiation in one mode are known as polarizing filters or simply "polarizerPolarizerA polarizer is an optical filter that passes light of a specific polarization and blocks waves of other polarizations. It can convert a beam of light of undefined or mixed polarization into a beam with well-defined polarization. The common types of polarizers are linear polarizers and circular...
s". In terms of the Stokes parameters, the total intensity is reduced while vectors in the Poincaré sphere are "dragged" towards the direction of the favored mode. Mathematically, under the treatment of the Stokes parameters as a Minkowski 4-vector, the transformation is a scaled Lorentz boost (due to the isomorphism of SL(2,C)Special linear groupIn mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
and the restricted Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
, SO(3,1)). Just as the Lorentz transformation preserves the proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
, the quantity det Ψ = S02 − S12 − S22 − S32 is invariant within a multiplicative scalar constant under Jones matrix transformations (dichroic and/or birefringent).
In birefringent and dichroic media, in addition to writing a Jones matrix for the net effect of passing through a particular path in a given medium, the evolution of the polarization state along that path can be characterized as the (matrix) product of an infinite series of infinitesimal steps, each operating on the state produced by all earlier matrices. In a uniform medium each step is the same, and one may write
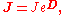
where J is an overall (real) gain/loss factor. Here D is a traceless matrix such that αDe gives the derivative of e with respect to z. If D is Hermitian the effect is dichroism, while a unitary matrix models birefringence. The matrix D can be expressed as a linear combination of the Pauli matrices, where real coefficients give Hermitian matrices and imaginary coefficients give unitary matrices. The Jones matrix in each case may therefore be written with the convenient construction
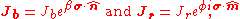
where σ is a 3-vector composed of the Pauli matrices (used here as generators for the Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
SL(2,C)) and n and m are real 3-vectors on the Poincaré sphere corresponding to one of the propagation modes of the medium. The effects in that space correspond to a Lorentz boost of velocity parameter 2β along the given direction, or a rotation of angle 2φ about the given axis. These transformations may also be written as biquaternions (quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s with complex elements), where the elements are related to the Jones matrix in the same way that the Stokes parameters are related to the coherency matrix. They may then be applied in pre- and post-multiplication to the quaternion representation of the coherency matrix, with the usual exploitation of the quaternion exponential for performing rotations and boosts taking a form equivalent to the matrix exponential equations above. (See Quaternion rotation)
In addition to birefringence and dichroism in extended media, polarization effects describable using Jones matrices can also occur at (reflective) interface between two materials of different refractive indexRefractive indexIn optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
. These effects are treated by the Fresnel equationsFresnel equationsThe Fresnel equations , deduced by Augustin-Jean Fresnel , describe the behaviour of light when moving between media of differing refractive indices...
. Part of the wave is transmitted and part is reflected, with the ratio depending on angle of incidence and the angle of refraction. In addition, if the plane of the reflecting surface is not aligned with the plane of propagation of the wave, the polarization of the two parts is altered. In general, the Jones matrices of the reflection and transmission are real and diagonalDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
, making the effect similar to that of a simple linear polarizer. For unpolarized light striking a surface at a certain optimum angle of incidence known as Brewster's angleBrewster's angleBrewster's angle is an angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. When unpolarized light is incident at this angle, the light that is reflected from the surface is therefore perfectly...
, the reflected wave will be completely s-polarized.
Certain effects do not produce linear transformations of the Jones vector, and thus cannot be described with (constant) Jones matrices. For these cases it is usual instead to use a 4×4 matrix that acts upon the Stokes 4-vector. Such matrices were first used by Paul Soleillet in 1929, although they have come to be known as Mueller matrices. While every Jones matrix has a Mueller matrix, the reverse is not true. Mueller matrices are frequently used to study the effects of the scatteringScatteringScattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
of waves from complex surfaces or ensembles of particles.
Polarization effects in everyday life
Light reflected by shiny transparent materials is partly or fully polarized, except when the light is perpendicular to the surface. It was through this effect that polarization was first discovered in 1808 by the mathematician Etienne Louis Malus. A polarizing filter, such as a pair of polarizing sunglasses
SunglassesSunglasses or sun glasses are a form of protective eyewear designed primarily to prevent bright sunlight and high-energy visible light from damaging or discomforting the eyes. They can sometimes also function as a visual aid, as variously termed spectacles or glasses exist, featuring lenses that...
, can be used to observe this effect by rotating the filter while looking through it at the reflection off of a distant horizontal surface. At certain rotation angles, the reflected light will be reduced or eliminated. Polarizing filters remove light polarized at 90° to the filter's polarization axis. If two polarizers are placed atop one another at 90° angles to one another, there is minimal light transmission.
Polarization by scattering is observed as light passes through the atmosphereEarth's atmosphereThe atmosphere of Earth is a layer of gases surrounding the planet Earth that is retained by Earth's gravity. The atmosphere protects life on Earth by absorbing ultraviolet solar radiation, warming the surface through heat retention , and reducing temperature extremes between day and night...
. The scatteredRayleigh scatteringRayleigh scattering, named after the British physicist Lord Rayleigh, is the elastic scattering of light or other electromagnetic radiation by particles much smaller than the wavelength of the light. The particles may be individual atoms or molecules. It can occur when light travels through...
light produces the brightness and color in clear skiesSkyThe sky is the part of the atmosphere or outer space visible from the surface of any astronomical object. It is difficult to define precisely for several reasons. During daylight, the sky of Earth has the appearance of a pale blue surface because the air scatters the sunlight. The sky is sometimes...
. This partial polarization of scattered light can be used to darken the sky in photographs, increasing the contrast. This effect is easiest to observe at sunsetSunsetSunset or sundown is the daily disappearance of the Sun below the horizon in the west as a result of Earth's rotation.The time of sunset is defined in astronomy as the moment the trailing edge of the Sun's disk disappears below the horizon in the west...
, on the horizon at a 90° angle from the setting sun. Another easily observed effect is the drastic reduction in brightness of images of the sky and clouds reflected from horizontal surfaces (see Brewster's angleBrewster's angleBrewster's angle is an angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection. When unpolarized light is incident at this angle, the light that is reflected from the surface is therefore perfectly...
), which is the main reason polarizing filters are often used in sunglasses. Also frequently visible through polarizing sunglasses are rainbowRainbowA rainbow is an optical and meteorological phenomenon that causes a spectrum of light to appear in the sky when the Sun shines on to droplets of moisture in the Earth's atmosphere. It takes the form of a multicoloured arc...
-like patterns caused by color-dependent birefringent effects, for example in toughened glassToughened glassToughened or tempered glass is a type of safety glass processed by controlled thermal or chemical treatments to increase its strength compared with normal glass. Tempering creates balanced internal stresses which cause the glass, when broken, to crumble into small granular chunks instead of...
(e.g., car windows) or items made from transparent plasticPlasticA plastic material is any of a wide range of synthetic or semi-synthetic organic solids used in the manufacture of industrial products. Plastics are typically polymers of high molecular mass, and may contain other substances to improve performance and/or reduce production costs...
s. The role played by polarization in the operation of liquid crystal displayLiquid crystal displayA liquid crystal display is a flat panel display, electronic visual display, or video display that uses the light modulating properties of liquid crystals . LCs do not emit light directly....
s (LCDs) is also frequently apparent to the wearer of polarizing sunglasses, which may reduce the contrast or even make the display unreadable.
The photograph on the right was taken through polarizing sunglasses and through the rear window of a car. Light from the sky is reflected by the windshield of the other car at an angle, making it mostly horizontally polarized. The rear window is made of tempered glass. Stress from heat treatment of the glass alters the polarization of light passing through it, like a wave plateWave plateA wave plate or retarder is an optical device that alters the polarization state of a light wave travelling through it.- Operation :A wave plate works by shifting the phase between two perpendicular polarization components of the light wave. A typical wave plate is simply a birefringent crystal...
. Without this effect, the sunglasses would block the horizontally polarized light reflected from the other car's window. The stress in the rear window, however, changes some of the horizontally polarized light into vertically polarized light that can pass through the glasses. As a result, the regular pattern of the heat treatment becomes visible.
Biology
Many animalAnimalAnimals are a major group of multicellular, eukaryotic organisms of the kingdom Animalia or Metazoa. Their body plan eventually becomes fixed as they develop, although some undergo a process of metamorphosis later on in their life. Most animals are motile, meaning they can move spontaneously and...
s are apparently capable of perceiving some of the components of the polarization of light, e.g. linear horizontally-polarized light. This is generally used for navigational purposes, since the linear polarization of sky light is always perpendicular to the direction of the sun. This ability is very common among the insectInsectInsects are a class of living creatures within the arthropods that have a chitinous exoskeleton, a three-part body , three pairs of jointed legs, compound eyes, and two antennae...
s, including beeBeeBees are flying insects closely related to wasps and ants, and are known for their role in pollination and for producing honey and beeswax. Bees are a monophyletic lineage within the superfamily Apoidea, presently classified by the unranked taxon name Anthophila...
s, which use this information to orient their communicative dancesBee learning and communicationHoney bees learn and communicate in order to find food sources and for other means.-Learning:Learning is essential for efficient foraging. Honey bees are unlikely to make many repeat visits if a plant provides little in the way of reward...
. Polarization sensitivity has also been observed in species of octopusOctopusThe octopus is a cephalopod mollusc of the order Octopoda. Octopuses have two eyes and four pairs of arms, and like other cephalopods they are bilaterally symmetric. An octopus has a hard beak, with its mouth at the center point of the arms...
, squidSquidSquid are cephalopods of the order Teuthida, which comprises around 300 species. Like all other cephalopods, squid have a distinct head, bilateral symmetry, a mantle, and arms. Squid, like cuttlefish, have eight arms arranged in pairs and two, usually longer, tentacles...
, cuttlefishCuttlefishCuttlefish are marine animals of the order Sepiida. They belong to the class Cephalopoda . Despite their name, cuttlefish are not fish but molluscs....
, and mantis shrimpMantis shrimpMantis shrimp or stomatopods are marine crustaceans, the members of the order Stomatopoda. They are neither shrimp nor mantids, but receive their name purely from the physical resemblance to both the terrestrial praying mantis and the shrimp. They may reach in length, although exceptional cases of...
. In the latter case, one species measures all six orthogonal components of polarization, and is believed to have optimal polarization vision. The rapidly changing, vividly colored skin patterns of cuttlefish, used for communication, also incorporate polarization patterns, and mantis shrimp are known to have polarization selective reflective tissue. Sky polarization was thought to be perceived by pigeons, which was assumed to be one of their aids in homingHoming pigeonThe homing pigeon is a variety of domestic pigeon derived from the Rock Pigeon selectively bred to find its way home over extremely long distances. The wild rock pigeon has an innate homing ability, meaning that it will generally return to its own nest and its own mate...
, but research indicates this is a popular myth.
The naked human eyeHuman eyeThe human eye is an organ which reacts to light for several purposes. As a conscious sense organ, the eye allows vision. Rod and cone cells in the retina allow conscious light perception and vision including color differentiation and the perception of depth...
is weakly sensitive to polarization, without the need for intervening filters. Polarized light creates a very faint pattern near the center of the visual field, called Haidinger's brushHaidinger's brushHaidinger's brush is an entoptic phenomenon first described by Austrianphysicist Wilhelm Karl von Haidinger in 1844.Many people are able to perceive polarization of light....
. This pattern is very difficult to see, but with practice one can learn to detect polarized light with the naked eye.
Geology
The property of (linear) birefringence is widespread in crystalline mineralMineralA mineral is a naturally occurring solid chemical substance formed through biogeochemical processes, having characteristic chemical composition, highly ordered atomic structure, and specific physical properties. By comparison, a rock is an aggregate of minerals and/or mineraloids and does not...
s, and indeed was pivotal in the initial discovery of polarization. In mineralogyMineralogyMineralogy is the study of chemistry, crystal structure, and physical properties of minerals. Specific studies within mineralogy include the processes of mineral origin and formation, classification of minerals, their geographical distribution, as well as their utilization.-History:Early writing...
, this property is frequently exploited using polarization microscopeMicroscopeA microscope is an instrument used to see objects that are too small for the naked eye. The science of investigating small objects using such an instrument is called microscopy...
s, for the purpose of identifying minerals. See optical mineralogyOptical mineralogyOptical mineralogy is the study of minerals and rocks by measuring their optical properties. Most commonly, rock and mineral samples are prepared as thin sections or grain mounts for study in the laboratory with a petrographic microscope...
for more details.
Chemistry
Polarization is principally of importance in chemistryChemistryChemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
due to circular dichroismCircular dichroismCircular dichroism refers to the differential absorption of left and right circularly polarized light. This phenomenon was discovered by Jean-Baptiste Biot, Augustin Fresnel, and Aimé Cotton in the first half of the 19th century. It is exhibited in the absorption bands of optically active chiral...
and "optical rotation" (circular birefringence) exhibited by optically active (chiralChirality (chemistry)A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom....
) molecules. It may be measured using polarimetryPolarimeterA polarimeter is a scientific instrument used to measure the angle of rotation caused by passing polarized light through an optically active substance....
.
The term "polarization" may also refer to the through-bond (inductiveInductive effectIn chemistry and physics, the inductive effect is an experimentally observable effect of the transmission of charge through a chain of atoms in a molecule by electrostatic induction...
or resonant effectResonance (chemistry)In chemistry, resonance or mesomerism is a way of describing delocalized electrons within certain molecules or polyatomic ions where the bonding cannot be expressed by one single Lewis formula...
) or through-space influence of a nearby functional group on the electronic properties (e.g. dipole momentElectric dipole momentIn physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...
) of a covalent bondCovalent bondA covalent bond is a form of chemical bonding that is characterized by the sharing of pairs of electrons between atoms. The stable balance of attractive and repulsive forces between atoms when they share electrons is known as covalent bonding....
or atom. This concept is based on the formation of an electric dipole within a molecule, which is related to polarization of electromagnetic waves in infrared spectroscopyInfrared spectroscopyInfrared spectroscopy is the spectroscopy that deals with the infrared region of the electromagnetic spectrum, that is light with a longer wavelength and lower frequency than visible light. It covers a range of techniques, mostly based on absorption spectroscopy. As with all spectroscopic...
. Molecules will absorb infrared light if the frequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
of the bond vibration is resonantResonance (chemistry)In chemistry, resonance or mesomerism is a way of describing delocalized electrons within certain molecules or polyatomic ions where the bonding cannot be expressed by one single Lewis formula...
with (identical to) the incident light frequency, where the molecular vibration at hand produces a change in the dipole momentBond dipole momentThe bond dipole moment uses the idea of electric dipole moment to measure the polarity of a chemical bond within a molecule. The bond dipole μ is given by:\mu = \delta \, d....
of the molecule. In some nonlinear optical processesNonlinear opticsNonlinear optics is the branch of optics that describes the behavior of light in nonlinear media, that is, media in which the dielectric polarization P responds nonlinearly to the electric field E of the light...
, the direction of an oscillating dipole will dictate the polarization of the emitted electromagnetic radiation, as in vibrational sum frequency generationSum frequency generationSum-frequency generation is a non-linear optical process. This phenomenon is based on the annihilation of two input photons at angular frequencies \omega_1 and \omega_2 while, simultaneously, one photon at frequency \omega_3 is generated...
spectroscopy or similar processes.
Polarized light does interact with anisotropicAnisotropyAnisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...
materials, which is the basis for birefringenceBirefringenceBirefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
. This is usually seen in crystalline materials and is especially useful in geologyGeologyGeology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
(see above). The polarized light is "double refracted", as the refractive index is different for horizontally and vertically polarized light in these materials. This is to say, the polarizabilityPolarizabilityPolarizability is the measure of the change in a molecule's electron distribution in response to an applied electric field, which can also be induced by electric interactions with solvents or ionic reagents. It is a property of matter...
of anisotropicAnisotropyAnisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...
materials is not equivalent in all directions. This anisotropy causes changes in the polarization of the incident beam, and is easily observable using cross-polar microscopy or polarimetryPolarimetryPolarimetry is the measurement and interpretation of the polarization of transverse waves, most notably electromagnetic waves, such as radio or light waves...
. The optical rotation of chiral compounds (as opposed to achiral compounds that form anisotropic crystals), is derived from circular birefringence. Like linear birefringence described above, circular birefringence is the "double refraction" of circular polarizedCircular polarizationIn electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
light.
Astronomy
In many areas of astronomyAstronomyAstronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, the study of polarized electromagnetic radiation from outer spaceOuter spaceOuter space is the void that exists between celestial bodies, including the Earth. It is not completely empty, but consists of a hard vacuum containing a low density of particles: predominantly a plasma of hydrogen and helium, as well as electromagnetic radiation, magnetic fields, and neutrinos....
is of great importance. Although not usually a factor in the thermal radiationThermal radiationThermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
of starStarA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s, polarization is also present in radiation from coherent astronomical sources (e.g. hydroxyl or methanol maserMaserA maser is a device that produces coherent electromagnetic waves through amplification by stimulated emission. Historically, “maser” derives from the original, upper-case acronym MASER, which stands for "Microwave Amplification by Stimulated Emission of Radiation"...
s), and incoherent sources such as the large radio lobes in active galaxies, and pulsar radio radiation (which may, it is speculated, sometimes be coherent), and is also imposed upon starlight by scattering from interstellar dust. Apart from providing information on sources of radiation and scattering, polarization also probes the interstellar magnetic field via Faraday rotation. The polarization of the cosmic microwave backgroundCosmic microwave background radiationIn cosmology, cosmic microwave background radiation is thermal radiation filling the observable universe almost uniformly....
is being used to study the physics of the very early universe. Synchrotron radiationSynchrotron radiationThe electromagnetic radiation emitted when charged particles are accelerated radially is called synchrotron radiation. It is produced in synchrotrons using bending magnets, undulators and/or wigglers...
is inherently polarised. It has been suggested that astronomical sources caused the chiralityChiralityChirality is a property of asymmetry important in several branches of science. It may refer to:* Chirality , a property of molecules having a non-superimposable mirror image...
of biological molecules on Earth.
3D movies
Polarization is also used for some 3D movies3-D filmA 3-D film or S3D film is a motion picture that enhances the illusion of depth perception...
, in which the images intended for each eye are either projected from two different projectors with orthogonally oriented polarizing filters or, more typically, from a single projector with time multiplexed polarization (a fast alternating polarization device for successive frames). Polarized 3D glasses with suitable polarized filters ensure that each eye receives only the intended image. Historical stereoscopicStereoscopyStereoscopy refers to a technique for creating or enhancing the illusion of depth in an image by presenting two offset images separately to the left and right eye of the viewer. Both of these 2-D offset images are then combined in the brain to give the perception of 3-D depth...
projection displays used linear polarization encoding because it was inexpensive and offered good separation. Circular polarization makes left-eye/right-eye separation insensitive to the viewing orientation; circular polarization is used in typical 3-D movie exhibition today, such as the system from RealDRealDRealD Inc. is the company that develops the RealD Cinema technology, used for projecting films in stereoscopic 3D using circularly polarized light. The company was founded in 2003 by Michael V. Lewis and Joshua Greer. Between 2005 and 2007 the company purchased StereoGraphics Inc...
. Polarized 3-D only works on screens that maintain polarization (such as silver screenSilver screenA silver screen, also known as a silver lenticular screen, is a type of projection screen that was popular in the early years of the motion picture industry and passed into popular usage as a metonym for the cinema industry...
s); a normal projection screen would cause depolarization which would void the effect.
Communication and radar applications
All radioRadioRadio is the transmission of signals through free space by modulation of electromagnetic waves with frequencies below those of visible light. Electromagnetic radiation travels by means of oscillating electromagnetic fields that pass through the air and the vacuum of space...
transmitting and receiving antennasAntenna (radio)An antenna is an electrical device which converts electric currents into radio waves, and vice versa. It is usually used with a radio transmitter or radio receiver...
are intrinsically polarized, special use of which is made in radarRadarRadar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
. Most antennas radiate either horizontal, vertical, or circular polarization although elliptical polarization also exists. The electric field or E-plane determines the polarization or orientation of the radio wave. Vertical polarization is most often used when it is desired to radiate a radio signal in all directions such as widely distributed mobile units. AM and FM radio use vertical polarization, while television uses horizontal polarization. Alternating vertical and horizontal polarization is used on satellite communications (including television satellites), to allow the satellite to carry two separate transmissions on a given frequency, thus doubling the number of customers a single satellite can serve. Electronically controlled birefringent devices are used in combination with polarizing filters as modulators in fiber optics.
Materials science
In engineeringEngineeringEngineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, the relationship between strainStrain (materials science)In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
and birefringenceBirefringenceBirefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
motivates the use of polarization in characterizing the distribution of stressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
and strain in prototypes.
Navigation
Sky polarization has been exploited in the "sky compass", which was used in the 1950s when navigating near the poles of the Earth's magnetic fieldEarth's magnetic fieldEarth's magnetic field is the magnetic field that extends from the Earth's inner core to where it meets the solar wind, a stream of energetic particles emanating from the Sun...
when neither the sunSunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
nor starStarA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s were visible (e.g. under daytime cloudCloudA cloud is a visible mass of liquid droplets or frozen crystals made of water and/or various chemicals suspended in the atmosphere above the surface of a planetary body. They are also known as aerosols. Clouds in Earth's atmosphere are studied in the cloud physics branch of meteorology...
or twilightTwilightTwilight is the time between dawn and sunrise or between sunset and dusk, during which sunlight scattering in the upper atmosphere illuminates the lower atmosphere, and the surface of the earth is neither completely lit nor completely dark. The sun itself is not directly visible because it is below...
). It has been suggested, controversially, that the VikingVikingThe term Viking is customarily used to refer to the Norse explorers, warriors, merchants, and pirates who raided, traded, explored and settled in wide areas of Europe, Asia and the North Atlantic islands from the late 8th to the mid-11th century.These Norsemen used their famed longships to...
s exploited a similar device (the "sunstoneIceland sparIceland spar, formerly known as Iceland crystal, is a transparent variety of calcite, or crystallized calcium carbonate, originally brought from Iceland, and used in demonstrating the polarization of light . It occurs in large readily cleavable crystals, easily divisible into rhombs, and is...
") in their extensive expeditions across the North Atlantic in the 9th–11th centuries, before the arrival of the magnetic compass in Europe in the 12th century. Related to the sky compass is the "polar clock", invented by Charles WheatstoneCharles WheatstoneSir Charles Wheatstone FRS , was an English scientist and inventor of many scientific breakthroughs of the Victorian era, including the English concertina, the stereoscope , and the Playfair cipher...
in the late 19th century.
Photography
In photographyPhotographyPhotography is the art, science and practice of creating durable images by recording light or other electromagnetic radiation, either electronically by means of an image sensor or chemically by means of a light-sensitive material such as photographic film...
, polarizing filterPolarizing filter (Photography)The polarizing filter used with most modern cameras is a circular polarizer. The first stage of the polarizer is a linear filter which filters out light that is linearly polarized in a specific direction...
s are used, mostly to improve the appearance of the sky (deeper blue, and clouds more visible):Other examples of polarization
- Shear waves in elastic materials exhibit polarization. These effects are studied as part of the field of seismologySeismologySeismology is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. The field also includes studies of earthquake effects, such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, oceanic,...
, where horizontal and vertical polarizations are termed SH and SV, respectively.
See also
- Polaroid (polarizer)
- Depolarizer (optics)Depolarizer (optics)A depolarizer or depolariser is an optical device used to scramble the polarization of light. An ideal depolarizer would output randomly polarized light whatever its input, but all practical depolarizers produce pseudo-random output polarization....
- Radial polarisationRadial polarisationA beam of light has radial polarization if at every position in the beam the polarization vector points towards the centre of the beam. In practice, an array of waveplates may be used to provide an approximation to a radially polarized beam...
- Rayleigh Sky ModelRayleigh sky modelThe Rayleigh sky model describes the observed polarization pattern of the daytime sky. Within the atmosphere Rayleigh scattering of light from air molecules, water, dust, and aerosols causes the sky's light to have a defined polarization pattern. The same elastic scattering processes cause the sky...
- Nicol prismNicol prismA Nicol prism is a type of polarizer, an optical device used to produce a polarized beam of light from an unpolarized beam. See polarized light. It was the first type of polarizing prism to be invented, in 1828 by William Nicol of Edinburgh...
- Photon polarizationPhoton polarizationPhoton polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
- Polarized light microscopyPolarized light microscopyPolarized light microscopy can mean any of a number of optical microscopy techniques involving polarized light. Simple techniques include illumination of the sample with polarized light. Directly transmitted light can, optionally, be blocked with a polariser orientated at 90 degrees to the...
- Kerr effectKerr effectThe Kerr effect, also called the quadratic electro-optic effect , is a change in the refractive index of a material in response to an applied electric field. The Kerr effect is distinct from the Pockels effect in that the induced index change is directly proportional to the square of the electric...
- Pockels effectPockels effectThe Pockels effect , or Pockels electro-optic effect, produces birefringence in an optical medium induced by a constant or varying electric field. It is distinguished from the Kerr effect by the fact that the birefringence is proportional to the electric field, whereas in the Kerr effect it is...
- Polarization rotatorPolarization rotatorA polarization rotator is an optical device that rotates the polarization axis of a linearly polarized light beam by an angle of choice. These rotators are either based on the principle of birefringence or on total internal reflection....
External links
- Polarized Light in Nature and Technology
- Polarized Light Digital Image Gallery: Microscopic images made using polarization effects
- Polarization by the University of Colorado Physics 2000: Animated explanation of polarization
- MathPages: The relationship between photon spin and polarization
- A virtual polarization microscope
- Polarization angle in satellite dishes.
- Using polarizers in photography
- Molecular Expressions: Science, Optics and You — Polarization of Light: Interactive Java tutorial
- Electromagnetic waves and circular dichroism: an animated tutorial
- HyperPhysics: Polarization concepts
- Tutorial on rotating polarization through waveplates (retarders)
- SPIE technical group on polarization
- A Java simulation on using polarizers
- Antenna Polarization
- Animations of Linear, Circular and Elliptical Polarizations on YouTube
- Shear waves in elastic materials exhibit polarization. These effects are studied as part of the field of seismology
-