Superpotential
Encyclopedia
Superpotential is a concept from particle physics
' supersymmetry
.
). Let W (the superpotential) be an arbitrary differentiable function of x and let the supersymmetric operators
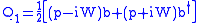
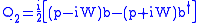
Note that Q1 and Q2 are self-adjoint. Let the Hamiltonian
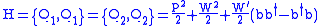
where W is the derivative of W. Also note that {Q1,Q2}=0. This is nothing other than N=2 supersymmetry.
Let's also call the spin down state "bosonic" and the spin up state "fermionic". This is only in analogy to quantum field theory and should not be taken literally. Then, Q1 and Q2 maps "bosonic" states into "fermionic" states and vice versa.
is given as the lowest component of a chiral superfield
, which is automatically complex.
The complex conjugate of a chiral superfield is an anti-chiral superfield.
To obtain the action from a set of superfields, the two choices are
1. Integrate a superfield on the whole superspace spanned by
and
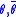
or
2. Integrate a chiral superfield on the chiral half of a superspace, spanned by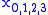
and
, not on 
.
Thus, given a set of chiral superfields and an arbitrary holomorphic function of them, W,
one can construct a term in the Lagrangian which is invariant under supersymmetry;
W cannot depend on the complex conjugates. The function W is called the superpotential.
The fact that W is holomorphic in the chiral superfields is the source of the tractability of
supersymmetric theories. Indeed, W is known to receive no perturbative corrections,
which is the celebrated perturbative non-renormalization theorem.
It is corrected by non-perturbative processes, e.g., by instanton
s.
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
' supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
.
Example of superpotentiality
Let's look at the example of a one dimensional nonrelativistic particle with a 2D (i.e. two state) internal degree of freedom called "spin" (it's not really spin because "real" spin is for particles in three-dimensional space). Let b be an operator which transforms a "spin up" particle into a "spin down" particle and its adjoint b† transforming a spin down particle into a spin up particle normalized such that the anticommutator {b,b†}=1. And of course, b2=0. Let p be the momentum of the particle and x be its position with [x,p]=i (let's use natural units where). 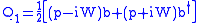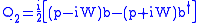Let W (the superpotential) be an arbitrary differentiable function of x and let the supersymmetric operatorsNote that Q1 and Q2 are self-adjoint. Let the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
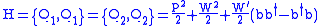
where W is the derivative of W. Also note that {Q1,Q2}=0. This is nothing other than N=2 supersymmetry.
Let's also call the spin down state "bosonic" and the spin up state "fermionic". This is only in analogy to quantum field theory and should not be taken literally. Then, Q1 and Q2 maps "bosonic" states into "fermionic" states and vice versa.
Superpotential in dimension 4
In supersymmetry in dimension 4, which might have some connection to the nature, a scalar field in the theoryis given as the lowest component of a chiral superfield
Chiral superfield
In theoretical physics, one often analyzes theories with supersymmetry in which chiral superfields play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using the notion of superspace...
, which is automatically complex.
The complex conjugate of a chiral superfield is an anti-chiral superfield.
To obtain the action from a set of superfields, the two choices are
1. Integrate a superfield on the whole superspace spanned by
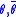
andor
2. Integrate a chiral superfield on the chiral half of a superspace, spanned by
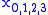
and
, not on .Thus, given a set of chiral superfields and an arbitrary holomorphic function of them, W,
one can construct a term in the Lagrangian which is invariant under supersymmetry;
W cannot depend on the complex conjugates. The function W is called the superpotential.
The fact that W is holomorphic in the chiral superfields is the source of the tractability of
supersymmetric theories. Indeed, W is known to receive no perturbative corrections,
which is the celebrated perturbative non-renormalization theorem.
It is corrected by non-perturbative processes, e.g., by instanton
Instanton
An instanton is a notion appearing in theoretical and mathematical physics. Mathematically, a Yang–Mills instanton is a self-dual or anti-self-dual connection in a principal bundle over a four-dimensional Riemannian manifold that plays the role of physical space-time in non-abelian gauge theory...
s.