D-term
Encyclopedia
In theoretical physics
, one often analyzes theories with supersymmetry
in which D-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace
. This superspace involves four extra fermionic coordinates
, transforming as a two-component spinor
and its conjugate.
Every superfield, i.e. a field that depends on all coordinates of the superspace, may be expanded with respect to the new fermionic coordinates. The generic kind of superfields, typically a vector superfield, indeed depend on all these coordinates. The last term in the corresponding expansion, namely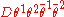
, is called the D-term.
Manifestly supersymmetric Lagrangian
s may also be written as integral
s over the whole superspace. Some special terms, such as the superpotential
, may be written as integrals over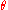
s only, which are known as F-term
s, and should be contrasted with the present D-terms.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, one often analyzes theories with supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
in which D-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace
Superspace
"Superspace" has had two meanings in physics. The word was first used by John Wheeler to describe the configuration space of general relativity; for example, this usage may be seen in his famous 1973 textbook Gravitation....
. This superspace involves four extra fermionic coordinates
, transforming as a two-component spinorSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
and its conjugate.
Every superfield, i.e. a field that depends on all coordinates of the superspace, may be expanded with respect to the new fermionic coordinates. The generic kind of superfields, typically a vector superfield, indeed depend on all these coordinates. The last term in the corresponding expansion, namely
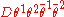, is called the D-term.Manifestly supersymmetric Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
s may also be written as integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s over the whole superspace. Some special terms, such as the superpotential
Superpotential
Superpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...
, may be written as integrals over
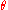s only, which are known as F-termF-term
In theoretical physics, one often analyzes theories with supersymmetry in which F-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
s, and should be contrasted with the present D-terms.