Dimensional reduction
Encyclopedia
In physics
, a theory in D spacetime
dimension
s can be redefined in a lower number of dimensions d, by taking all the fields to be independent of the location in the extra D − d dimensions.
Dimensional reduction is the limit of a compactified theory
where the size of the compact dimension goes to zero. For example, consider a periodic compact dimension with period L. Let x be the coordinate along this dimension. Any field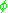
can be described as a sum of the following terms:
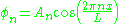
with An a constant. According to quantum mechanics
, such a term has momentum
nh/L along x, where h is Planck's constant. Therefore as L goes to zero, the momentum goes to infinity, as so is the energy
, unless n = 0. However n = 0 gives a field which is constant with respect to x. So at this limit, and at finite energy,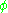
will not depend on x.
Let us generalize this argument. The compact dimension imposes specific boundary conditions on all fields, for example periodic boundary conditions in the case of a periodic dimension, and typically Neumann
or Dirichlet boundary condition
s in other cases. Now suppose the size of the compact dimension is L; Then the possible eigenvalues under gradient
along this dimension are integer or half-integer multiples of 1/L (depending on the precise boundary conditions). In quantum mechanics this eigenvalue is the momentum of the field, and is therefore related to its energy. As L → 0 all eigenvalues except zero go to infinity, and so does the energy. Therefore at this limit, with finite energy, zero is the only possible eigenvalue under gradient along the compact dimension, meaning that nothing depends on this dimension.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a theory in D spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s can be redefined in a lower number of dimensions d, by taking all the fields to be independent of the location in the extra D − d dimensions.
Dimensional reduction is the limit of a compactified theory
Compactification (physics)
In physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic....
where the size of the compact dimension goes to zero. For example, consider a periodic compact dimension with period L. Let x be the coordinate along this dimension. Any field
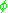can be described as a sum of the following terms: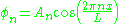with An a constant. According to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, such a term has momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
nh/L along x, where h is Planck's constant. Therefore as L goes to zero, the momentum goes to infinity, as so is the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, unless n = 0. However n = 0 gives a field which is constant with respect to x. So at this limit, and at finite energy,
will not depend on x.Let us generalize this argument. The compact dimension imposes specific boundary conditions on all fields, for example periodic boundary conditions in the case of a periodic dimension, and typically Neumann
Neumann boundary condition
In mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
or Dirichlet boundary condition
Dirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
s in other cases. Now suppose the size of the compact dimension is L; Then the possible eigenvalues under gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
along this dimension are integer or half-integer multiples of 1/L (depending on the precise boundary conditions). In quantum mechanics this eigenvalue is the momentum of the field, and is therefore related to its energy. As L → 0 all eigenvalues except zero go to infinity, and so does the energy. Therefore at this limit, with finite energy, zero is the only possible eigenvalue under gradient along the compact dimension, meaning that nothing depends on this dimension.
See also
- Compactification (physics)Compactification (physics)In physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic....
- Kaluza–Klein theoryKaluza–Klein theoryIn physics, Kaluza–Klein theory is a model that seeks to unify the two fundamental forces of gravitation and electromagnetism. The theory was first published in 1921. It was proposed by the mathematician Theodor Kaluza who extended general relativity to a five-dimensional spacetime...
- String theory#Extra dimensions
- SupergravitySupergravityIn theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...