Korteweg–de Vries equation
Encyclopedia
In mathematics
, the Korteweg–de Vries equation (KdV equation for short) is a mathematical model
of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation
whose solutions can be exactly and precisely specified. The solutions in turn include prototypical examples of soliton
s. KdV can be solved by means of the inverse scattering transform
. The mathematical theory behind the KdV equation is rich and interesting, and, in the broad sense, is a topic of active mathematical research. The equation is named for Diederik Korteweg
and Gustav de Vries
who studied it in , though the equation first appears in .
for a function
φ of two real
variables, space x and time t :
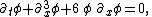
with ∂x and ∂t denoting partial derivative
s with respect to x and t.
The constant 6 in front of the last term is conventional but of no great significance: multiplying t, x, and φ by constants can be used to make the coefficients of any of the three terms equal to any given non-zero constants.
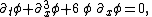
or, integrating with respect to x,
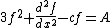
where A is a constant of integration. Interpreting the independent variable x above as a time variable, this means f satisfies Newton's equation of motion
in a cubic potential. If parameters are adjusted so that the potential function V(x) has local maximum at x=0, there is a solution in which f(x) starts at this point at 'time' -∞, eventually slides down to the local minimum, then back up the other side, reaching an equal height, then reverses direction, ending up at the local maximum again at time ∞. In other words, f(x) approaches 0 as x→±∞. This is the characteristic shape of the solitary wave
solution.
More precisely, the solution is
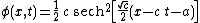
where a is an arbitrary constant. This describes a right-moving soliton
.
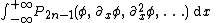
where the polynomials Pn are defined recursively by
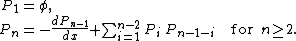
The first few integrals of motion are:
Only the odd-numbered terms P(2n+1) result in non-trivial (meaning non-zero) integrals of motion .
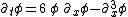
can be reformulated as the Lax equation
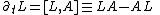
with L a Sturm–Liouville operator:
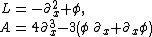
and this accounts for the infinite number of first integrals of the KdV equation.
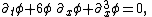
is the Euler-Lagrange equation
of motion for the Lagrangian density,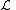
with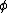
defined by
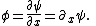
Since the Lagrangian (eq (1)) contains second derivatives, the Euler–Lagrange equation of motion for this field is
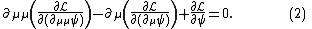
where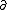
is a derivative with respect to the 
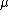component.
A sum over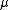
is implied so eq (2) really reads,
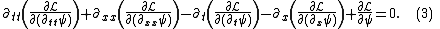
Evaluate the five terms of eq (3) by plugging in eq (1),
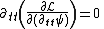
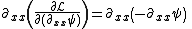
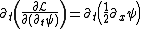
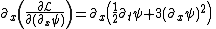
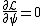
Remember the definition
, so use that to simplify the above terms,
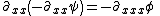
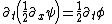
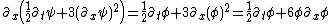
Finally, plug these three non-zero terms back into eq (3) to see
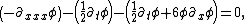
which is exactly the KdV equation
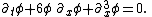
in 1834, followed by theoretical investigations by Lord Rayleigh and Joseph Boussinesq around 1870 and, finally, Korteweg and De Vries in 1895.
The KdV equation was not studied much after this until
, discovered numerically that its solutions seemed to decompose at large times into a collection of "solitons": well separated solitary waves. Moreover the solitons seems to be almost unaffected in shape by passing through each other (though this could cause a change in their position). They also made the connection to earlier numerical experiments by Fermi, Pasta, and Ulam by showing that the KdV equation was the continuum limit of the FPU
system. Development of the analytic solution by means of the inverse scattering transform
was done in 1967 by Gardner, Greene, Kruskal and Miura.
in the continuum limit, it approximately describes the evolution of long, one-dimensional waves in many physical settings, including:
The KdV equation can also be solved using the inverse scattering transform
such as those applied to the non-linear Schrödinger equation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Korteweg–de Vries equation (KdV equation for short) is a mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
whose solutions can be exactly and precisely specified. The solutions in turn include prototypical examples of soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s. KdV can be solved by means of the inverse scattering transform
Inverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
. The mathematical theory behind the KdV equation is rich and interesting, and, in the broad sense, is a topic of active mathematical research. The equation is named for Diederik Korteweg
Diederik Korteweg
Diederik Johannes Korteweg was a Dutch mathematician. He is now remembered as the joint discoverer of the Korteweg–de Vries equation.-Early life and education:...
and Gustav de Vries
Gustav de Vries
Gustav de Vries was a Dutch mathematician, who is best remembered for his work on the Korteweg–de Vries equation with Diederik Korteweg. He was born on 22 January 1866 in Amsterdam, and studied at the University of Amsterdam with the distinguished physical chemist Johannes van der Waals and with...
who studied it in , though the equation first appears in .
Definition
The KdV equation is a nonlinear, dispersive partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
for a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
φ of two real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variables, space x and time t :
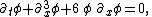
with ∂x and ∂t denoting partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s with respect to x and t.
The constant 6 in front of the last term is conventional but of no great significance: multiplying t, x, and φ by constants can be used to make the coefficients of any of the three terms equal to any given non-zero constants.
Soliton solutions
Consider solutions in which a fixed wave form (given by f(x)) maintains its shape as it travels to the right at phase speed c. Such a solution is given by φ(x,t) = f(x-ct). Substituting it into the KdV equation gives the ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
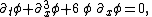
or, integrating with respect to x,
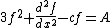
where A is a constant of integration. Interpreting the independent variable x above as a time variable, this means f satisfies Newton's equation of motion
Equation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
in a cubic potential. If parameters are adjusted so that the potential function V(x) has local maximum at x=0, there is a solution in which f(x) starts at this point at 'time' -∞, eventually slides down to the local minimum, then back up the other side, reaching an equal height, then reverses direction, ending up at the local maximum again at time ∞. In other words, f(x) approaches 0 as x→±∞. This is the characteristic shape of the solitary wave
Solitary wave
In mathematics and physics, a solitary wave can refer to* The solitary wave or wave of translation, as observed by John Scott Russell in the Union Canal, near Edinburgh in 1834...
solution.
More precisely, the solution is
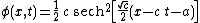
where a is an arbitrary constant. This describes a right-moving soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
.
Integrals of motion
The KdV equation has infinitely many integrals of motion , which do not change with time. They can be given explicitly as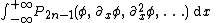where the polynomials Pn are defined recursively by
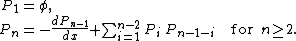
The first few integrals of motion are:
- the momentum
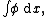
- the energy
-
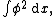
Only the odd-numbered terms P(2n+1) result in non-trivial (meaning non-zero) integrals of motion .
Lax pairs
The KdV equation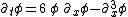can be reformulated as the Lax equation
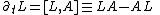
with L a Sturm–Liouville operator:
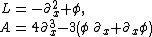
and this accounts for the infinite number of first integrals of the KdV equation.
Lagrangian
The Korteweg–de Vries equation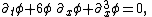is the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
of motion for the Lagrangian density,
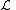
with
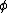defined by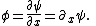Since the Lagrangian (eq (1)) contains second derivatives, the Euler–Lagrange equation of motion for this field is
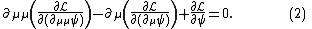
where
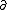is a derivative with respect to the 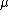component.A sum over
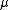is implied so eq (2) really reads,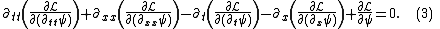Evaluate the five terms of eq (3) by plugging in eq (1),
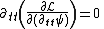
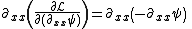
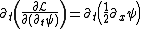
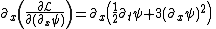
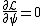
Remember the definition
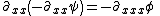
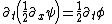
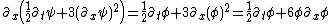
, so use that to simplify the above terms,Finally, plug these three non-zero terms back into eq (3) to see
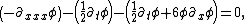
which is exactly the KdV equation
Long-time asymptotics
It can be shown that any sufficiently fast decaying smooth solution will eventually split into a finite superposition of solitons travelling to the right plus a decaying dispersive part travelling to the left. This was first observed by and can be rigorously proven using the nonlinear steepest descent analysis for oscillatory Riemann-Hilbert problems.History
The history of the KdV equation started with experiments by John Scott RussellJohn Scott Russell
John Scott Russell was a Scottish naval engineer who built the Great Eastern in collaboration with Isambard Kingdom Brunel, and made the discovery that gave birth to the modern study of solitons.-Personal life:John Scott Russell was born John Russell on 9 May 1808 in Parkhead, Glasgow, the son of...
in 1834, followed by theoretical investigations by Lord Rayleigh and Joseph Boussinesq around 1870 and, finally, Korteweg and De Vries in 1895.
The KdV equation was not studied much after this until
, discovered numerically that its solutions seemed to decompose at large times into a collection of "solitons": well separated solitary waves. Moreover the solitons seems to be almost unaffected in shape by passing through each other (though this could cause a change in their position). They also made the connection to earlier numerical experiments by Fermi, Pasta, and Ulam by showing that the KdV equation was the continuum limit of the FPU
Fermi–Pasta–Ulam problem
In physics, the Fermi–Pasta–Ulam problem or FPU problem was the apparent paradox in chaos theory that many complicated enough physical systems exhibited almost exactly periodic behavior instead of ergodic behavior. One of the resolutions of the paradox includes the insight that many non-linear...
system. Development of the analytic solution by means of the inverse scattering transform
Inverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
was done in 1967 by Gardner, Greene, Kruskal and Miura.
Applications and connections
The KdV equation has several connections to physical problems. In addition to being the governing equation of the string in the Fermi–Pasta–Ulam problemFermi–Pasta–Ulam problem
In physics, the Fermi–Pasta–Ulam problem or FPU problem was the apparent paradox in chaos theory that many complicated enough physical systems exhibited almost exactly periodic behavior instead of ergodic behavior. One of the resolutions of the paradox includes the insight that many non-linear...
in the continuum limit, it approximately describes the evolution of long, one-dimensional waves in many physical settings, including:
- shallow-water waves with weakly non-linear restoring forces,
- long internal waves in a density-stratified oceanOceanAn ocean is a major body of saline water, and a principal component of the hydrosphere. Approximately 71% of the Earth's surface is covered by ocean, a continuous body of water that is customarily divided into several principal oceans and smaller seas.More than half of this area is over 3,000...
, - ion-acoustic waves in a plasmaPlasma (physics)In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
, - acousticAcousticsAcoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
waves on a crystal lattice, - and more.
The KdV equation can also be solved using the inverse scattering transform
Inverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
such as those applied to the non-linear Schrödinger equation.
Variations
Many different variations of the KdV equations have been studied. Some are listed in the following table.| Name | Equation |
|---|---|
| Korteweg–de Vries (KdV) |  |
| KdV (cylindrical) |  |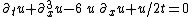
| KdV (deformed) |  |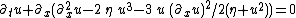
| KdV (generalized) |  |
| KdV (generalized) Generalized Korteweg-de Vries equation In mathematics the generalized Korteweg-de Vries equation is the nonlinear partial differential equation\partial_t u + \partial_x^3 u + \partial_x f = 0.\,The function f... |
 |
| KdV (Lax 7th) |  |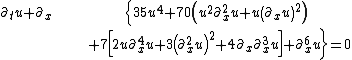
| KdV (modified) |  |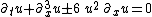
| KdV (modified modified) |  |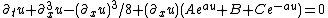
| KdV (spherical) |  |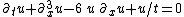
| KdV (super) |  , |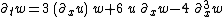
| KdV (transitional) |  |
| KdV (variable coefficients) |  |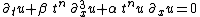
| Korteweg-de Vries-Burgers equation |  |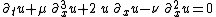
See also
- Benjamin–Bona–Mahony equation
- Boussinesq approximation (water waves)Boussinesq approximation (water waves)In fluid dynamics, the Boussinesq approximation for water waves is an approximation valid for weakly non-linear and fairly long waves. The approximation is named after Joseph Boussinesq, who first derived them in response to the observation by John Scott Russell of the wave of translation...
- Cnoidal waveCnoidal waveIn fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves...
- Dispersion (water waves)Dispersion (water waves)In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
- Dispersionless equationDispersionless equationDispersionless limits of integrable partial differential equations arise in various problems of mathematics and physics and are intensively studied in the recent literature .-Dispersionless KP equation:...
- Kadomtsev–Petviashvili equation
- Novikov–Veselov equationNovikov–Veselov equationIn mathematics, the Novikov–Veselov equation is a natural -dimensional analogue of the Korteweg–de Vries equation. Unlike another -dimensional analogue of KdV, the Kadomtsev–Petviashvili equation, it is integrable via the inverse scattering transform for the 2-dimensional stationary Schrödinger...
- Ursell numberUrsell numberIn fluid dynamics, the Ursell number indicates the nonlinearity of long surface gravity waves on a fluid layer. This dimensionless parameter is named after Fritz Ursell, who discussed its significance in 1953....
- Vector solitonVector solitonIn physical optics or wave optics, a vector soliton is a solitary wave with multiple components coupled together that maintains its shape during propagation. Ordinary solitons maintain their shape but have effectively only one polarization component, while vector solitons have two distinct...
External links
- Korteweg–de Vries equation at EqWorld: The World of Mathematical Equations.
- Korteweg–de Vries equation at NEQwiki, the nonlinear equations encyclopedia.
- Cylindrical Korteweg–de Vries equation at EqWorld: The World of Mathematical Equations.
- Modified Korteweg–de Vries equation at EqWorld: The World of Mathematical Equations.
- Modified Korteweg–de Vries equation at NEQwiki, the nonlinear equations encyclopedia.
- Derivation of the Korteweg–de Vries equation for a narrow canal.
- Three Solitons Solution of KdV Equation - http://www.youtube.com/watch?v=H4rN3Wr4ctw
- Three Solitons (unstable) Solution of KdV Equation - http://www.youtube.com/watch?v=5z5SylS2QHE
- Mathematical aspects of equations of Korteweg-de Vries type are discussed on the Dispersive PDE Wiki.
- Solitons from the Korteweg-de Vries Equation by S. M. Blinder, The Wolfram Demonstrations Project.
- Solitons & Nonlinear Wave Equations