Dispersionless equation
Encyclopedia
Dispersionless limits of integrable partial differential equations (PDE) arise in various problems of mathematics and physics and are intensively studied in the recent literature (see, f.i., [1]-[5]).
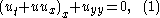
It arises from the commutation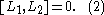
of the following pair of 1-parameter families of vector fields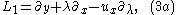
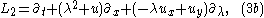
where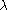
is a spectral parameter. The dKPE is the 
-dispersionless limit of the celebrated Kadomtsev–Petviashvili equation.
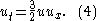
It is the dispersionless or quasiclassical limit of the Korteweg–de Vries equation
.
:
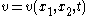where the following standard notation of complex analysis is used:
, 
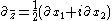. The function 
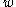here is an auxiliary function defined via 
up to a holomorphic summand. The function 
is generally assumed to be a real-valued function.
Dispersionless KP equation
The dispersionless Kadomtsev–Petviashvili equation (dKPE) has the form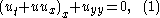It arises from the commutation
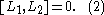
of the following pair of 1-parameter families of vector fields
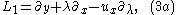
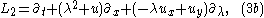
where
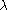is a spectral parameter. The dKPE is the -dispersionless limit of the celebrated Kadomtsev–Petviashvili equation.Dispersionless Korteweg–de Vries equation
The dispersionless Korteweg–de Vries equation (dKdVE) reads as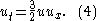It is the dispersionless or quasiclassical limit of the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
.
Dispersionless Novikov–Veselov equation
The dispersionless Novikov-Veselov equation is most commonly written as the following equation on function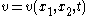:where the following standard notation of complex analysis is used:
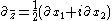, . The function 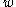here is an auxiliary function defined via up to a holomorphic summand. The function is generally assumed to be a real-valued function.See also
- Integrable systems
- Nonlinear Schrödinger equationNonlinear Schrödinger equationIn theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
- Nonlinear systems
- Davey–Stewartson equationDavey–Stewartson equationIn fluid dynamics, the Davey–Stewartson equation was introduced in a paper by to describe the evolution of a three-dimensional wave-packet on water of finite depth....
- Dispersive partial differential equationDispersive partial differential equationIn mathematics, a dispersive partial differential equation or dispersive PDE is a partial differential equation that is dispersive. In this context, dispersion means that waves of different wavelength propagate at different phase velocities....
- Kadomtsev–Petviashvili equation
- Korteweg–de Vries equationKorteweg–de Vries equationIn mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
External links
- Ishimori_system at the dispersive equations wiki