
Kadomtsev–Petviashvili equation
Encyclopedia
In mathematics
, the Kadomtsev–Petviashvili equation (named after Boris Borisovich Kadomtsev and Vladimir Iosifovich Petviashvili) is a partial differential equation
. The KP equation is usually written as: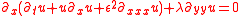
where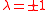 . The above form shows that the KP equation is a generalization to two spatial dimensions, x and y, of the one-dimensional Korteweg–de Vries (KdV) equation
. The above form shows that the KP equation is a generalization to two spatial dimensions, x and y, of the one-dimensional Korteweg–de Vries (KdV) equation
.
Like the KdV equation, the KP equation is completely integrable. It can also be solved using the inverse scattering transform
much like the nonlinear Schrödinger equation
.
with weakly non-linear restoring forces and frequency dispersion
. If surface tension
is weak compared to gravitational forces
,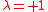 is used; if surface tension is strong, then
is used; if surface tension is strong, then 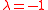 . Because of the asymmetry in the way x- and y-terms enter the equation, the waves described by the KP equation behave differently in the direction of propagation (x-direction) and transverse (y) direction; oscillations in the y-direction tend to be smoother (be of small-deviation).
. Because of the asymmetry in the way x- and y-terms enter the equation, the waves described by the KP equation behave differently in the direction of propagation (x-direction) and transverse (y) direction; oscillations in the y-direction tend to be smoother (be of small-deviation).
The KP equation can also be used to model waves in ferromagnetic
media, as well as two-dimensional matter–wave pulses in Bose–Einstein condensate
s.
 , typical x-dependent oscillations have a wavelength of
, typical x-dependent oscillations have a wavelength of 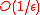 giving a singular limiting regime as
giving a singular limiting regime as  . The limit
. The limit  is called the dispersion
is called the dispersion
less limit.
If we also assume that the solutions are independent of y as , then they also satisfy Burgers' equation
, then they also satisfy Burgers' equation
: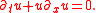
Suppose the amplitude of oscillations of a solution is asymptotically small —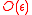 — in the dispersionless limit. Then the amplitude satisfies a mean-field equation of Davey–Stewartson type.
— in the dispersionless limit. Then the amplitude satisfies a mean-field equation of Davey–Stewartson type.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Kadomtsev–Petviashvili equation (named after Boris Borisovich Kadomtsev and Vladimir Iosifovich Petviashvili) is a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
. The KP equation is usually written as:
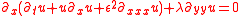
where
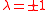 . The above form shows that the KP equation is a generalization to two spatial dimensions, x and y, of the one-dimensional Korteweg–de Vries (KdV) equation
. The above form shows that the KP equation is a generalization to two spatial dimensions, x and y, of the one-dimensional Korteweg–de Vries (KdV) equationKorteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
.
Like the KdV equation, the KP equation is completely integrable. It can also be solved using the inverse scattering transform
Inverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
much like the nonlinear Schrödinger equation
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
.
History
The KP equation was first written in 1970 by Soviet physicists Boris B. Kadomtsev (1928–1998) and Vladimir I. Petviashvili (1936–1993); it came as a natural generalization of the KdV equation (derived by Korteweg and De Vries in 1895). Whereas in the KdV equation waves are strictly one-dimensional, in the KP equation this restriction is relaxed. Still, both in the KdV and the KP equation, waves have to travel in the positive x-direction.Connections to physics
The KP equation can be used to model water waves of long wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
with weakly non-linear restoring forces and frequency dispersion
Dispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
. If surface tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
is weak compared to gravitational forces
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
,
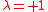 is used; if surface tension is strong, then
is used; if surface tension is strong, then 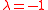 . Because of the asymmetry in the way x- and y-terms enter the equation, the waves described by the KP equation behave differently in the direction of propagation (x-direction) and transverse (y) direction; oscillations in the y-direction tend to be smoother (be of small-deviation).
. Because of the asymmetry in the way x- and y-terms enter the equation, the waves described by the KP equation behave differently in the direction of propagation (x-direction) and transverse (y) direction; oscillations in the y-direction tend to be smoother (be of small-deviation).The KP equation can also be used to model waves in ferromagnetic
Ferromagnetism
Ferromagnetism is the basic mechanism by which certain materials form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished...
media, as well as two-dimensional matter–wave pulses in Bose–Einstein condensate
Bose–Einstein condensate
A Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at...
s.
Limiting behavior
For , typical x-dependent oscillations have a wavelength of
, typical x-dependent oscillations have a wavelength of 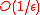 giving a singular limiting regime as
giving a singular limiting regime as  . The limit
. The limit  is called the dispersion
is called the dispersionDispersion
Dispersion may refer to:In physics:*The dependence of wave velocity on frequency or wavelength:**Dispersion , for light waves**Dispersion **Acoustic dispersion, for sound waves...
less limit.
If we also assume that the solutions are independent of y as
 , then they also satisfy Burgers' equation
, then they also satisfy Burgers' equationBurgers' equation
Burgers' equation is a fundamental partial differential equation from fluid mechanics. It occurs in various areas of applied mathematics, such as modeling of gas dynamics and traffic flow...
:
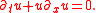
Suppose the amplitude of oscillations of a solution is asymptotically small —
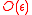 — in the dispersionless limit. Then the amplitude satisfies a mean-field equation of Davey–Stewartson type.
— in the dispersionless limit. Then the amplitude satisfies a mean-field equation of Davey–Stewartson type.

