
Benjamin–Bona–Mahony equation
Encyclopedia
The Benjamin–Bona–Mahony equation (or BBM equation) is the partial differential equation
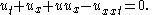
This equation was introduced in as an improvement of the Korteweg–de Vries equation
(KdV equation) for modeling long waves of small amplitude in 1+1 dimensions. They show the stability and uniqueness of solutions to the BBM equation. This contrasts with the KdV equation, which is unstable in its high wavenumber
components. Further, while the KdV equation has an infinite number of integrals of motion, the BBM equation only has three.
A higher-dimensional version is given by

where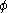 is a fixed smooth function from
is a fixed smooth function from 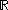 to
to 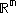 . proved local existence of a solution in all dimensions.
. proved local existence of a solution in all dimensions.
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
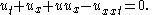
This equation was introduced in as an improvement of the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
(KdV equation) for modeling long waves of small amplitude in 1+1 dimensions. They show the stability and uniqueness of solutions to the BBM equation. This contrasts with the KdV equation, which is unstable in its high wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
components. Further, while the KdV equation has an infinite number of integrals of motion, the BBM equation only has three.
A higher-dimensional version is given by

where
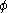 is a fixed smooth function from
is a fixed smooth function from 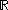 to
to 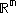 . proved local existence of a solution in all dimensions.
. proved local existence of a solution in all dimensions.

