
Boussinesq approximation (water waves)
Encyclopedia
In fluid dynamics
, the Boussinesq approximation for water waves is an approximation
valid for weakly non-linear and fairly long waves. The approximation is named after Joseph Boussinesq, who first derived them in response to the observation by John Scott Russell
of the wave of translation (also known as solitary wave
or soliton
). The 1872 paper of Boussinesq introduces the equations now known as the Boussinesq equations.
The Boussinesq approximation for water waves takes into account the vertical structure of the horizontal and vertical flow velocity
. This results in non-linear partial differential equations, called Boussinesq-type equations, which incorporate frequency dispersion
(as opposite to the shallow water equations
, which are not frequency-dispersive). In coastal engineering, Boussinesq-type equations are frequently used in computer models for the simulation
of water waves in shallow
sea
s and harbours.
This elimination of the vertical coordinate was first done by Joseph Boussinesq in 1871, to construct an approximate solution for the solitary wave (or wave of translation). Subsequently, in 1872, Boussinesq derived the equations known nowadays as the Boussinesq equations.
The steps in the Boussinesq approximation are:
Thereafter, the Boussinesq approximation is applied to the remaining flow equations, in order to eliminate the dependence on the vertical coordinate.
As a result, the resulting partial differential equations are in terms of functions
of the horizontal coordinates (and time
).
As an example, consider potential flow
over a horizontal bed in the (x,z) plane, with x the horizontal and z the vertical coordinate. The bed is located at z = -h, where h is the mean
water depth. A Taylor expansion is made of the velocity potential φ(x,z,t) around the bed level z = -h:
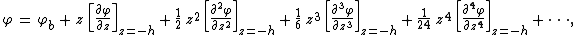
where φb(x,t) is the velocity potential at the bed. Invoking Laplace's equation
for φ, as valid for incompressible flow
, gives:
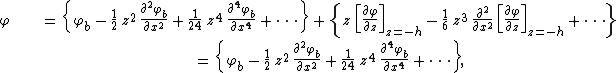
since the vertical velocity ∂φ / ∂z is zero at the — impermeable — horizontal bed z = -h. This series may subsequently be truncated to a finite number of terms.
elevation z = η(x,t) are:
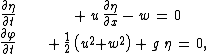
where:
Now the Boussinesq approximation for the velocity potential φ, as given above, is applied in these boundary conditions. Further, in the resulting equations only the linear
and quadratic
terms with respect to η and ub are retained (with ub = ∂φb / ∂x the horizontal velocity at the bed z = -h). The cubic and higher order terms are assumed to be negligible
. Then, the following partial differential equations are obtained:
set A — Boussinesq (1872), equation (25)
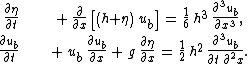
This set of equations has been derived for a flat horizontal bed, i.e. the mean depth h is a constant independent of position x. When the right-hand sides of the above equations are set to zero, they reduce to the shallow water equations
.
Under some additional approximations, but at the same order of accuracy, the above set A can be reduced to a single partial differential equation
for the free surface
elevation η:
set B — Boussinesq (1872), equation (26)
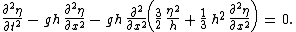
From the terms between brackets, the importance of nonlinearity of the equation can be expressed in terms of the Ursell number
.
In dimensionless quantities, using the water depth h and gravitational acceleration g for non-dimensionalization, this equation reads, after normalization
:
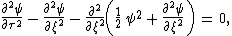
with:
. For the case of infinitesimal
wave amplitude
, the terminology is linear frequency dispersion. The frequency dispersion characteristics of a Boussinesq-type of equation can be used to determine the range of wave lengths, for which it is a valid approximation
.
The linear frequency dispersion
characteristics for the above set A of equations are:
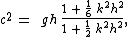
with:
The relative error in the phase speed c for set A, as compared with linear theory for water waves
, is less than 4% for a relative wave number kh < ½ π. So, in engineering
applications, set A is valid for wavelengths λ larger than 4 times the water depth h.
The linear frequency dispersion
characteristics of equation B are:
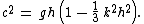
The relative error in the phase speed for equation B is less than 4% for kh < 2π / 7, equivalent to wave lengths λ longer than 7 times the water depth h, called fairly long waves.
For short waves with k2 h2 > 3 equation B become physically meaningless, because there are no longer real-valued solutions of the phase speed.
The original set of two partial differential equations (Boussinesq, 1872, equation 25, see set A above) does not have this shortcoming.
The shallow water equations
have a relative error in the phase speed less than 4% for wave lengths λ in excess of 13 times the water depth h.
Some directions, into which the Boussinesq equations have been extended, are:
Besides solitary
wave solutions, the Korteweg–de Vries equation also has periodic and exact solutions, called cnoidal wave
s. These are approximate solutions of the Boussinesq equation.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the Boussinesq approximation for water waves is an approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
valid for weakly non-linear and fairly long waves. The approximation is named after Joseph Boussinesq, who first derived them in response to the observation by John Scott Russell
John Scott Russell
John Scott Russell was a Scottish naval engineer who built the Great Eastern in collaboration with Isambard Kingdom Brunel, and made the discovery that gave birth to the modern study of solitons.-Personal life:John Scott Russell was born John Russell on 9 May 1808 in Parkhead, Glasgow, the son of...
of the wave of translation (also known as solitary wave
Solitary wave
In mathematics and physics, a solitary wave can refer to* The solitary wave or wave of translation, as observed by John Scott Russell in the Union Canal, near Edinburgh in 1834...
or soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
). The 1872 paper of Boussinesq introduces the equations now known as the Boussinesq equations.
The Boussinesq approximation for water waves takes into account the vertical structure of the horizontal and vertical flow velocity
Flow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
. This results in non-linear partial differential equations, called Boussinesq-type equations, which incorporate frequency dispersion
Dispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
(as opposite to the shallow water equations
Shallow water equations
The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid .The equations are derived from depth-integrating the Navier–Stokes...
, which are not frequency-dispersive). In coastal engineering, Boussinesq-type equations are frequently used in computer models for the simulation
Simulation
Simulation is the imitation of some real thing available, state of affairs, or process. The act of simulating something generally entails representing certain key characteristics or behaviours of a selected physical or abstract system....
of water waves in shallow
Waves and shallow water
When waves travel into areas of shallow water, they begin to be affected by the ocean bottom. The free orbital motion of the water is disrupted, and water particles in orbital motion no longer return to their original position. As the water becomes shallower, the swell becomes higher and steeper,...
sea
Sea
A sea generally refers to a large body of salt water, but the term is used in other contexts as well. Most commonly, it means a large expanse of saline water connected with an ocean, and is commonly used as a synonym for ocean...
s and harbours.
Boussinesq approximation
The essential idea in the Boussinesq approximation is the elimination of the vertical coordinate from the flow equations, while retaining some of the influences of the vertical structure of the flow under water waves. This is useful because the waves propagate in the horizontal plane and have a different (not wave-like) behaviour in the vertical direction. Often, as in Boussinesq's case, the interest is primarily in the wave propagation.This elimination of the vertical coordinate was first done by Joseph Boussinesq in 1871, to construct an approximate solution for the solitary wave (or wave of translation). Subsequently, in 1872, Boussinesq derived the equations known nowadays as the Boussinesq equations.
The steps in the Boussinesq approximation are:
- a Taylor expansion is made of the horizontal and vertical flow velocityFlow velocityIn fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
(or velocity potential) around a certain elevationElevationThe elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface ....
, - this Taylor expansion is truncated to a finite number of terms,
- the conservation of mass (see continuity equationContinuity equationA continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
) for an incompressible flowIncompressible flowIn fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
and the zero-curl condition for an irrotational flow are used, to replace vertical partial derivatives of quantities in the Taylor expansion with horizontal partial derivatives.
Thereafter, the Boussinesq approximation is applied to the remaining flow equations, in order to eliminate the dependence on the vertical coordinate.
As a result, the resulting partial differential equations are in terms of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the horizontal coordinates (and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
).
As an example, consider potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
over a horizontal bed in the (x,z) plane, with x the horizontal and z the vertical coordinate. The bed is located at z = -h, where h is the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
water depth. A Taylor expansion is made of the velocity potential φ(x,z,t) around the bed level z = -h:
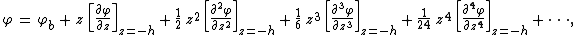
where φb(x,t) is the velocity potential at the bed. Invoking Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
for φ, as valid for incompressible flow
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
, gives:
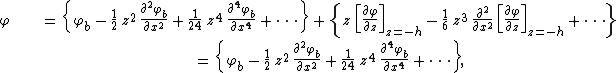
since the vertical velocity ∂φ / ∂z is zero at the — impermeable — horizontal bed z = -h. This series may subsequently be truncated to a finite number of terms.
Derivation
For water waves on an incompressible fluid and irrotational flow in the (x,z) plane, the boundary conditions at the free surfaceFree surface
In physics, a free surface is the surface of a fluid that is subject to constant perpendicular normal stress and zero parallel shear stress,such as the boundary between two homogenous fluids,for example liquid water and the air in the Earth's atmosphere...
elevation z = η(x,t) are:
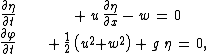
where:
- u is the horizontal flow velocityFlow velocityIn fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
component: u = ∂φ / ∂x, - w is the vertical flow velocityFlow velocityIn fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
component: w = ∂φ / ∂z, - g is the accelerationAccelerationIn physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
by gravity.
Now the Boussinesq approximation for the velocity potential φ, as given above, is applied in these boundary conditions. Further, in the resulting equations only the linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
and quadratic
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
terms with respect to η and ub are retained (with ub = ∂φb / ∂x the horizontal velocity at the bed z = -h). The cubic and higher order terms are assumed to be negligible
Negligible
Negligible refers to the quantities so small that they can be ignored when studying the larger effect. Although related to the more mathematical concepts of infinitesimal, the idea of negligibility is particularly useful in practical disciplines like physics, chemistry, mechanical and electronic...
. Then, the following partial differential equations are obtained:
set A — Boussinesq (1872), equation (25)
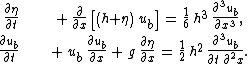
This set of equations has been derived for a flat horizontal bed, i.e. the mean depth h is a constant independent of position x. When the right-hand sides of the above equations are set to zero, they reduce to the shallow water equations
Shallow water equations
The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid .The equations are derived from depth-integrating the Navier–Stokes...
.
Under some additional approximations, but at the same order of accuracy, the above set A can be reduced to a single partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
for the free surface
Free surface
In physics, a free surface is the surface of a fluid that is subject to constant perpendicular normal stress and zero parallel shear stress,such as the boundary between two homogenous fluids,for example liquid water and the air in the Earth's atmosphere...
elevation η:
set B — Boussinesq (1872), equation (26)
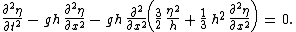
From the terms between brackets, the importance of nonlinearity of the equation can be expressed in terms of the Ursell number
Ursell number
In fluid dynamics, the Ursell number indicates the nonlinearity of long surface gravity waves on a fluid layer. This dimensionless parameter is named after Fritz Ursell, who discussed its significance in 1953....
.
In dimensionless quantities, using the water depth h and gravitational acceleration g for non-dimensionalization, this equation reads, after normalization
Normalization
Normalization may refer to:- Mathematics and statistics:* Normalization property , term in mathematical logic and theoretical computer science* Noether normalization lemma, result of commutative algebra...
:
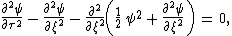
with:
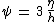 |
: the dimensionless surface elevation, |
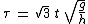 |
: the dimensionless time, and |
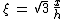 |
: the dimensionless horizontal position. |
Linear frequency dispersion
Water waves of different wave lengths travel with different phase speeds, a phenomenon known as frequency dispersionDispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
. For the case of infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
wave amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
, the terminology is linear frequency dispersion. The frequency dispersion characteristics of a Boussinesq-type of equation can be used to determine the range of wave lengths, for which it is a valid approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
.
The linear frequency dispersion
Dispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
characteristics for the above set A of equations are:
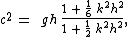
with:
- c the phase speed,
- k the wave number( k = 2π / λ, with λ the wave length).
The relative error in the phase speed c for set A, as compared with linear theory for water waves
Airy wave theory
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational...
, is less than 4% for a relative wave number kh < ½ π. So, in engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
applications, set A is valid for wavelengths λ larger than 4 times the water depth h.
The linear frequency dispersion
Dispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
characteristics of equation B are:
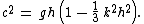
The relative error in the phase speed for equation B is less than 4% for kh < 2π / 7, equivalent to wave lengths λ longer than 7 times the water depth h, called fairly long waves.
For short waves with k2 h2 > 3 equation B become physically meaningless, because there are no longer real-valued solutions of the phase speed.
The original set of two partial differential equations (Boussinesq, 1872, equation 25, see set A above) does not have this shortcoming.
The shallow water equations
Shallow water equations
The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid .The equations are derived from depth-integrating the Navier–Stokes...
have a relative error in the phase speed less than 4% for wave lengths λ in excess of 13 times the water depth h.
Extensions
There are an overwhelming number of mathematical models which are referred to as Boussinesq equations. This may easily lead to confusion, since often they are loosely referenced to as the Boussinesq equations, while in fact a variant thereof is considered. So it is more appropriate to call them Boussinesq-type equations. Strictly speaking, the Boussinesq equations is the above mentioned set B, since it is used in the analysis in the remainder of his 1872 paper.Some directions, into which the Boussinesq equations have been extended, are:
- varying bathymetryBathymetryBathymetry is the study of underwater depth of lake or ocean floors. In other words, bathymetry is the underwater equivalent to hypsometry. The name comes from Greek βαθύς , "deep", and μέτρον , "measure"...
, - improved frequency dispersionDispersion (water waves)In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
, - improved non-linear behavior,
- making a Taylor expansion around different vertical elevations,
- dividing the fluid domain in layers, and applying the Boussinesq approximation in each layer separately,
- inclusion of wave breaking,
- inclusion of surface tensionSurface tensionSurface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
, - extension to internal waves on an interfaceInterface (chemistry)An interface is a surface forming a common boundary among two different phases, such as an insoluble solid and a liquid, two immiscible liquids or a liquid and an insoluble gas. The importance of the interface depends on which type of system is being treated: the bigger the quotient area/volume,...
between fluid domains of different mass density, - derivation from a variational principleVariational principleA variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
.
Further approximations for one-way wave propagation
While the Boussinesq equations allow for waves traveling simultaneously in opposing directions, it is often advantageous to only consider waves traveling in one direction. Under small additional assumptions, the Boussinesq equations reduce to:- the Korteweg–de Vries equationKorteweg–de Vries equationIn mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
for wave propagationWave propagationWave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
in one horizontal dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, - the Kadomtsev–Petviashvili equation for wave propagationWave propagationWave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
in two horizontal dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s, - the nonlinear Schrödinger equationNonlinear Schrödinger equationIn theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
(NLS equation) for the complex valuedComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
amplitudeAmplitudeAmplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of narrowbandNarrowbandIn radio, narrowband describes a channel in which the bandwidth of the message does not significantly exceed the channel's coherence bandwidth. It is a common misconception that narrowband refers to a channel which occupies only a "small" amount of space on the radio spectrum.The opposite of...
waves (slowly modulated waves).
Besides solitary
Solitary
Solitary is the state of being alone. The term may refer to:* shortened form of solitary confinement in jail* Solitary but social, a type of social organization in biology where individuals forage alone but share sleeping space...
wave solutions, the Korteweg–de Vries equation also has periodic and exact solutions, called cnoidal wave
Cnoidal wave
In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves...
s. These are approximate solutions of the Boussinesq equation.

