
Generalized Korteweg-de Vries equation
Encyclopedia
In mathematics the generalized Korteweg-de Vries equation is the nonlinear partial differential equation
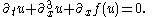
The function f
is sometimes taken to be f(u)= uk+1/(k+1) + u for some positive integer k (where the extra u is a "drift term" that makes the analysis a little easier). The case f(u) = 3u2 is the original
Korteweg–de Vries equation
.
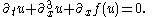
The function f
is sometimes taken to be f(u)= uk+1/(k+1) + u for some positive integer k (where the extra u is a "drift term" that makes the analysis a little easier). The case f(u) = 3u2 is the original
Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
.

