Novikov–Veselov equation
Encyclopedia
In mathematics
, the Novikov–Veselov equation (or Veselov–Novikov equation) is a natural (2+1)-dimensional analogue of the Korteweg–de Vries (KdV) equation
. Unlike another (2+1)-dimensional analogue of KdV, the Kadomtsev–Petviashvili equation, it is integrable
via the inverse scattering transform
for the 2-dimensional stationary Schrödinger equation
. Similarly, the Korteweg–de Vries equation is integrable via the inverse scattering transform for the 1-dimensional Schrödinger equation. The equation is named after S.P. Novikov and A.P. Veselov who published it in .
where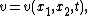
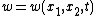and the following standard notation of complex analysis
is used: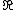
is the real part
,
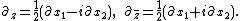
The function
is generally considered to be real-valued. The function 
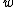is an auxiliary function defined via 
up to a holomorphic
summand,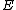
is a real parameter corresponding to the energy level of the related 2-dimensional Schrödinger equation
and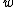 
in the Novikov–Veselov equation depend only on one spatial variable, e.g. 
, 
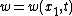, then the equation is reduced to the classical Korteweg–de Vries equation
. If in the Novikov–Veselov equation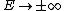
, then the equation reduces to another (2+1)-dimensional analogue of the KdV equation, the Kadomtsev–Petviashvili equation (to KP-I and KP-II, respectively) .
s (PDEs) begins with the discovery of C.S. Gardner, J.M. Greene, M.D. Kruskal, R.M. Miura
, who demonstrated that the Korteweg–de Vries equation can be integrated via the inverse scattering problem for the 1-dimensional stationary Schrödinger equation. The algebraic nature of this discovery was revealed by Lax
who showed that the Korteweg–de Vries equation can be written in the following operator form (the so-called Lax pair
):
where
, 
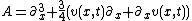and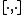 
is a commutator
. Equation is a compatibility condition for the equations
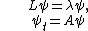
for all values of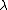
.
Afterwards, a representation of the form was found for many other physically interesting nonlinear equations, like the Kadomtsev–Petviashvili equation, sine-Gordon equation
, nonlinear Schrödinger equation
and others. This led to an extensive development of the theory of inverse scattering transform for integrating nonlinear partial differential equations.
When trying to generalize representation to two dimensions, one obtains that it holds only for trivial cases (operators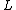
, 
, 
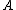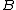have constant coefficients or operator 
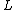is a differential operator of order not larger than 1 with respect to one of the variables). However, S.V. Manakov showed that in the two-dimensional case it is more correct to consider the following representation (further called the Manakov L-A-B triple):
or, equivalently, to search for the condition of compatibility of the equations
at one fixed value of parameter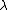
.
Representation for the 2-dimensional Schrödinger operator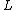
was found by S.P. Novikov and A.P. Veselov in . The authors also constructed a hierarchy of evolution equations integrable via the inverse scattering transform for the 2-dimensional Schrödinger equation at fixed energy. This set of evolution equations (which is sometimes called the hierarchy of the Novikov–Veselov equations) contains, in particular, the equation .
s. For example, the scattering data of the Grinevich–Zakharov
soliton solutions of the Novikov–Veselov equation have singular points.
Solitons are traditionally a key object of study in the theory of nonlinear integrable equations. The solitons of the Novikov-Veselov equation at positive energy are transparent potentials, similarly to the one-dimensional case (in which solitons are reflectionless potentials). However, unlike the one-dimensional case where there exist well-known exponentially decaying solitons, the Novikov–Veselov equation (at least at non-zero energy) does not possess exponentially localized solitons .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Novikov–Veselov equation (or Veselov–Novikov equation) is a natural (2+1)-dimensional analogue of the Korteweg–de Vries (KdV) equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
. Unlike another (2+1)-dimensional analogue of KdV, the Kadomtsev–Petviashvili equation, it is integrable
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
via the inverse scattering transform
Inverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
for the 2-dimensional stationary Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. Similarly, the Korteweg–de Vries equation is integrable via the inverse scattering transform for the 1-dimensional Schrödinger equation. The equation is named after S.P. Novikov and A.P. Veselov who published it in .
Definition
The Novikov–Veselov equation is most commonly written aswhere
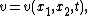
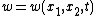and the following standard notation of complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
is used:
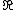is the real partReal and imaginary parts
In mathematics, a hypercomplex number has a real part and an imaginary part associated with it. This is most familiar in the context of complex numbers, but extends to the other hypercomplex algebras such as split-complex numbers and quaternions....
,
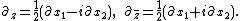
The function
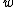is generally considered to be real-valued. The function is an auxiliary function defined via up to a holomorphicHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
summand,
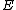is a real parameter corresponding to the energy level of the related 2-dimensional Schrödinger equationRelation to other nonlinear integrable equations
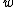When the functions and in the Novikov–Veselov equation depend only on one spatial variable, e.g. , , 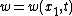then the equation is reduced to the classical Korteweg–de Vries equationKorteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
. If in the Novikov–Veselov equation
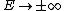, then the equation reduces to another (2+1)-dimensional analogue of the KdV equation, the Kadomtsev–Petviashvili equation (to KP-I and KP-II, respectively) .History
The inverse scattering transform method for solving nonlinear partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s (PDEs) begins with the discovery of C.S. Gardner, J.M. Greene, M.D. Kruskal, R.M. Miura
Robert M. Miura
Robert M. Miura is a Distinguished Professor of Mathematical Sciences and of Biomedical Engineering at New Jersey Institute of Technology in Newark, New Jersey.-Education:...
, who demonstrated that the Korteweg–de Vries equation can be integrated via the inverse scattering problem for the 1-dimensional stationary Schrödinger equation. The algebraic nature of this discovery was revealed by Lax
Peter Lax
Peter David Lax is a mathematician working in the areas of pure and applied mathematics. He has made important contributions to integrable systems, fluid dynamics and shock waves, solitonic physics, hyperbolic conservation laws, and mathematical and scientific computing, among other fields...
who showed that the Korteweg–de Vries equation can be written in the following operator form (the so-called Lax pair
Lax pair
In mathematics, in the theory of integrable systems, a Lax pair is a pair of time-dependent matrices or operators that describe the corresponding differential equations. They were introduced by Peter Lax to discuss solitons in continuous media...
):
where
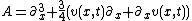, and 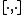is a commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
. Equation is a compatibility condition for the equations
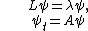
for all values of
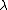.Afterwards, a representation of the form was found for many other physically interesting nonlinear equations, like the Kadomtsev–Petviashvili equation, sine-Gordon equation
Sine-Gordon equation
The sine–Gordon equation is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d'Alembert operator and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative...
, nonlinear Schrödinger equation
Nonlinear Schrödinger equation
In theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
and others. This led to an extensive development of the theory of inverse scattering transform for integrating nonlinear partial differential equations.
When trying to generalize representation to two dimensions, one obtains that it holds only for trivial cases (operators
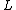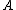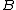, , have constant coefficients or operator 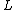is a differential operator of order not larger than 1 with respect to one of the variables). However, S.V. Manakov showed that in the two-dimensional case it is more correct to consider the following representation (further called the Manakov L-A-B triple):or, equivalently, to search for the condition of compatibility of the equations
at one fixed value of parameter
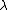.Representation for the 2-dimensional Schrödinger operator
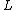was found by S.P. Novikov and A.P. Veselov in . The authors also constructed a hierarchy of evolution equations integrable via the inverse scattering transform for the 2-dimensional Schrödinger equation at fixed energy. This set of evolution equations (which is sometimes called the hierarchy of the Novikov–Veselov equations) contains, in particular, the equation .Physical applications
The dispersionless version of the Novikov–Veselov equation was derived in a model of nonlinear geometrical optics .Behavior of solutions
The behavior of solutions to the Novikov–Veselov equation depends essentially on the regularity of the scattering data for this solution. If the scattering data are regular, then the solution vanishes uniformly with time. If the scattering data have singularities, then the solution may develop solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s. For example, the scattering data of the Grinevich–Zakharov
Vladimir E. Zakharov
Vladimir Evgen'evich Zakharov is a Soviet and Russian mathematician and physicist. He is currently Regents' Professor of mathematics at The University of Arizona and director of the Mathematical Physics Sector at the Lebedev Physical Institute...
soliton solutions of the Novikov–Veselov equation have singular points.
Solitons are traditionally a key object of study in the theory of nonlinear integrable equations. The solitons of the Novikov-Veselov equation at positive energy are transparent potentials, similarly to the one-dimensional case (in which solitons are reflectionless potentials). However, unlike the one-dimensional case where there exist well-known exponentially decaying solitons, the Novikov–Veselov equation (at least at non-zero energy) does not possess exponentially localized solitons .