
Writhe
Encyclopedia
In knot theory
, the writhe is a property of an oriented link
diagram. The writhe is the total number of positive crossings minus the total number of negative crossings.
A direction is assigned to the link at a point in each component and this direction is followed all the way around each component. If as you travel along a link component and cross over a crossing, the strand underneath goes from right to left, the crossing is positive; if the lower strand goes from left to right, the crossing is negative. One way of remembering this is to use a variation of the right-hand rule
.
For a knot diagram, using the right-hand rule with either orientation gives the same result, so the writhe is well-defined on unoriented knot diagrams.
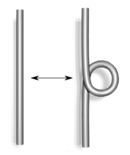 The writhe of a knot is unaffected by two of the three Reidemeister moves: moves of Type II and Type III do not affect the writhe. Reidemeister move Type I, however, increases or decreases the writhe by 1. This implies that the writhe of a knot is not an isotopy invariant of the knot itself — only the diagram. By a series of Type I moves one can set the writhe of a diagram for a given knot to be any integer at all.
The writhe of a knot is unaffected by two of the three Reidemeister moves: moves of Type II and Type III do not affect the writhe. Reidemeister move Type I, however, increases or decreases the writhe by 1. This implies that the writhe of a knot is not an isotopy invariant of the knot itself — only the diagram. By a series of Type I moves one can set the writhe of a diagram for a given knot to be any integer at all.
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the writhe is a property of an oriented link
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
diagram. The writhe is the total number of positive crossings minus the total number of negative crossings.
A direction is assigned to the link at a point in each component and this direction is followed all the way around each component. If as you travel along a link component and cross over a crossing, the strand underneath goes from right to left, the crossing is positive; if the lower strand goes from left to right, the crossing is negative. One way of remembering this is to use a variation of the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
.
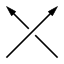 |
 |
|
| Positive crossing |
Negative crossing |
For a knot diagram, using the right-hand rule with either orientation gives the same result, so the writhe is well-defined on unoriented knot diagrams.


