
Pretzel link
Encyclopedia

Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pretzel link is a special kind of link
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
. A pretzel link which is also a knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
(i.e. a link with one component) is a pretzel knot.
In the standard projection of the
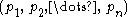 pretzel link, there are
pretzel link, there are 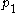 left-handed crossings in the first tangle
left-handed crossings in the first tangleTangle
Tangle may refer to:*Tangle , an Australian television series*tangle.com, a Christian social networking site*Tangle theory, a branch of knot theory invented by John Horton Conway*Sea tangle, another name for kelp...
,
 in the second, and, in general,
in the second, and, in general, 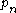 in the nth.
in the nth.A pretzel link can also be described as a Montesinos link with integer tangles.
Some basic results
The pretzel link is a knot
pretzel link is a knotKnot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
both
 and all the
and all the  are odd
are oddEven and odd numbers
In mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
or exactly one of the
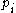 is even.
is even.The
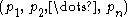 pretzel link is split
pretzel link is splitSplit link
In the mathematical field of knot theory, a split link is a link that has a 2-sphere in its complement separating one or more link components from the others. A split link is said to be splittable, and a link that is not split is called a non-split link or not splittable...
if at least two of the
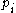 are zero
are zero0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
; but the converse
Converse (logic)
In logic, the converse of a categorical or implicational statement is the result of reversing its two parts. For the implication P → Q, the converse is Q → P. For the categorical proposition All S is P, the converse is All P is S. In neither case does the converse necessarily follow from...
is false.
The
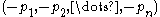 pretzel link is the mirror image
pretzel link is the mirror imageMirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
of the
 pretzel link.
pretzel link.The
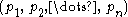 pretzel link is link-equivalent (i.e. homotopy-equivalent in S3
pretzel link is link-equivalent (i.e. homotopy-equivalent in S33-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
) to the
 pretzel link. Thus, too, the
pretzel link. Thus, too, the 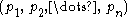 pretzel link is link-equivalent to the
pretzel link is link-equivalent to the 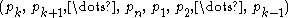 pretzel link.
pretzel link.The
 pretzel link is link-equivalent to the
pretzel link is link-equivalent to the 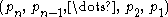 pretzel link. However, if one orients the links in a canonical way, then these two links have opposite orientations.
pretzel link. However, if one orients the links in a canonical way, then these two links have opposite orientations.Some examples
The (−1, −1, −1) pretzel knot is the trefoilTrefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
; the (0, 3, −1) pretzel knot is its mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
.
The (5, −1, −1) pretzel knot is the stevedore knot
Stevedore knot (mathematics)
In knot theory, the stevedore knot is one of three prime knots with crossing number six, the others being the 62 knot and the 63 knot. The stevedore knot is listed as the 61 knot in the Alexander–Briggs notation, and it can also be described as a twist knot with four twists, or as the pretzel...
(61).
If p, q, r are distinct odd integers greater than 1, then the (p, q, r) pretzel knot is a non-invertible knot.
The (2p,\ 2q, 2r) pretzel link is a link formed by three linked unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
s.
The (−3, 0, −3) pretzel knot is the connected sum of two trefoil knot
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
s.
The (0, q, 0) pretzel link is the split union
Split link
In the mathematical field of knot theory, a split link is a link that has a 2-sphere in its complement separating one or more link components from the others. A split link is said to be splittable, and a link that is not split is called a non-split link or not splittable...
of an unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
and another knot.
Utility
(−2, 3, 2n + 1) pretzel links are especially useful in the study of 3-manifold3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s. Many results have been stated about the manifolds that result from Dehn surgery
Dehn surgery
In topology, a branch of mathematics, a Dehn surgery, named after Max Dehn, is a specific construction used to modify 3-manifolds. The process takes as input a 3-manifold together with a link...
on the (−2,3,7) pretzel knot in particular.
Pretzel knots can be used to introduce students to the essentials of knot theory by making edible pretzels.

