
Stevedore knot (mathematics)
Encyclopedia

Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the stevedore knot is one of three prime knot
Prime knot
In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
s with crossing number
Crossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
six, the others being the 62 knot
6₂ knot
In knot theory, the 62 knot is one of three prime knots with crossing number six, the others being the stevedore knot and the 63 knot. This knot is sometimes referred to as the Miller Institute knot, because is appears in the logo of the Miller Institute for Basic Research in Science at the...
and the 63 knot
6₃ knot
In knot theory, the 63 knot is one of three prime knots with crossing number six, the others being the stevedore knot and the 62 knot.Like the figure-eight knot, the 63 knot is amphichiral, meaning that it is indistinguishable from its own mirror image...
. The stevedore knot is listed as the 61 knot in the Alexander–Briggs notation, and it can also be described as a twist knot
Twist knot
In knot theory, a branch of mathematics, a twist knot is a knot obtained by repeatedly twisting a closed loop and then linking the ends together...
with four twists, or as the (5,−1,−1) pretzel knot.
The mathematical stevedore knot is named after the common stevedore knot, which is often used as a stopper
Stopper (knot)
The term stopper knot has three distinct meanings in the context of knotting and cordage.-At the end of a line:A stopper knot is tied at the end of a rope to prevent the end from unraveling, slipping through another knot, or passing back through a hole, block, or belay/rappel device...
at the end of a rope
Rope
A rope is a length of fibres, twisted or braided together to improve strength for pulling and connecting. It has tensile strength but is too flexible to provide compressive strength...
. The mathematical version of the knot can be obtained from the common version by joining together the two loose ends of the rope, forming a knotted loop
Loop (topology)
In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...
.
The stevedore knot is invertible
Invertible knot
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant...
but not amphichiral
Amphichiral knot
In the mathematical field of knot theory, a chiral knot is a knot that is not equivalent to its mirror image. An oriented knot that is equivalent to its mirror image is an amphichiral knot, also called an achiral knot or amphicheiral knot. The chirality of a knot is a knot invariant...
. Its Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
is
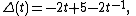
its Conway polynomial
Conway polynomial
In mathematics, Conway polynomial can refer to:* the Alexander–Conway polynomial in knot theory* the Conway polynomial...
is
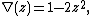
and its Jones polynomial is

The Alexander polynomial and Conway polynomial are the same as those for the knot 946, but the Jones polynomials for these two knots are different. Because the Alexander polynomial is not monic, the stevedore knot is not fibered
Fibered knot
A knot or link Kin the 3-dimensional sphere S^3 is called fibered or fibred if there is a 1-parameter family F_t of Seifert surfaces for K, where the parameter t runs through the points of the unit circle S^1, such that if s is not equal to t...
.
The stevedore knot is a ribbon knot
Ribbon knot
In the mathematical area of knot theory, a ribbon knot is a knot that bounds a self-intersecting disc with only ribbon singularities. This type of singularity is a self-intersection along an arc; the preimage of this arc consists of two arcs in the disc, one properly embedded in the disc and the...
, and is therefore also a slice knot.
The stevedore knot is a hyperbolic knot, with its complement having a volume
Hyperbolic volume (knot)
In the mathematical field of knot theory, the hyperbolic volume of a hyperbolic link is simply the volume of the link's complement with respect to its complete hyperbolic metric. The volume is necessarily finite. The hyperbolic volume of a non-hyperbolic knot is often defined to be zero...
of approximately 3.16396.
See also
- Figure-eight knot (mathematics)Figure-eight knot (mathematics)In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This is the smallest possible crossing number except for the unknot and trefoil knot...
- Knot theoryKnot theoryIn topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...

