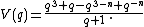Twist knot
Encyclopedia
In knot theory
, a branch of mathematics
, a twist knot is a knot obtained by repeatedly twisting a closed loop
and then linking the ends together. (That is, a twist knot is any Whitehead double of an unknot.) The twist knots are an infinite family of knots, and are considered the simplest type of knots after the torus knot
s.
one, since the knot can be untied by unlinking the two ends. Every twist knot is also a 2-bridge knot
. Of the twist knots, only the unknot
and the stevedore knot
are slice knots. A twist knot with half-twists has crossing number
half-twists has crossing number
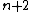 . All twist knots are invertible
. All twist knots are invertible
, but the only amphichiral
twist knots are the unknot and the figure-eight knot
.
 of half-twists. The Alexander polynomial
of half-twists. The Alexander polynomial
of a twist knot is given by the formula
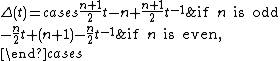
and the Conway polynomial
is
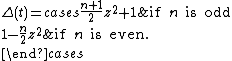
When is odd, the Jones polynomial is
is odd, the Jones polynomial is
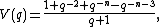
and when is even, it is
is even, it is
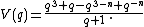
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a twist knot is a knot obtained by repeatedly twisting a closed loop
Loop (topology)
In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...
and then linking the ends together. (That is, a twist knot is any Whitehead double of an unknot.) The twist knots are an infinite family of knots, and are considered the simplest type of knots after the torus knot
Torus knot
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
s.
Construction
A twist knot is obtained by linking together the two ends of a twisted loop. Any number of half-twists may be introduced into the loop before linking, resulting in an infinite family of possibilities. The following figures show the first few twist knots:Properties
All twist knots have unknotting numberUnknotting number
In the mathematical area of knot theory, the unknotting number of a knot is the minimum number of times the knot must be passed through itself to untie it. If a knot has unknotting number n, then there exists a diagram of the knot which can be changed to unknot by switching n crossings...
one, since the knot can be untied by unlinking the two ends. Every twist knot is also a 2-bridge knot
2-bridge knot
In the mathematical field of knot theory, a 2-bridge knot is a knot which can be isotoped so that the natural height function given by the z-coordinate has only two maxima and two minima as critical points....
. Of the twist knots, only the unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
and the stevedore knot
Stevedore knot (mathematics)
In knot theory, the stevedore knot is one of three prime knots with crossing number six, the others being the 62 knot and the 63 knot. The stevedore knot is listed as the 61 knot in the Alexander–Briggs notation, and it can also be described as a twist knot with four twists, or as the pretzel...
are slice knots. A twist knot with
 half-twists has crossing number
half-twists has crossing numberCrossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
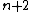 . All twist knots are invertible
. All twist knots are invertibleInvertible knot
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant...
, but the only amphichiral
Amphichiral knot
In the mathematical field of knot theory, a chiral knot is a knot that is not equivalent to its mirror image. An oriented knot that is equivalent to its mirror image is an amphichiral knot, also called an achiral knot or amphicheiral knot. The chirality of a knot is a knot invariant...
twist knots are the unknot and the figure-eight knot
Figure-eight knot (mathematics)
In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This is the smallest possible crossing number except for the unknot and trefoil knot...
.
Invariants
The invariants of a twist knot depend on the number of half-twists. The Alexander polynomial
of half-twists. The Alexander polynomialAlexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
of a twist knot is given by the formula
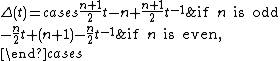
and the Conway polynomial
Conway polynomial
In mathematics, Conway polynomial can refer to:* the Alexander–Conway polynomial in knot theory* the Conway polynomial...
is
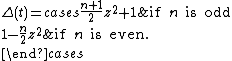
When
 is odd, the Jones polynomial is
is odd, the Jones polynomial is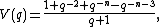
and when
 is even, it is
is even, it is